
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи теории управленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
К практическим занятиям по дисциплине "Теория управления" (для студентов специальности "Прикладная математика")
У Т В Е Р Ж Д Е Н О На заседании кафедры прикладная математика Протокол № от
Луганск 2013 Министерство образования и науки,
Восточноукраинский национальный университет имени Владимира Даля
Методические рекомендации к самостоятельной и практической работе по дисциплине "Теория управления" (для студентов специальности "Прикладная математика")
У Т В Е Р Ж Д Е Н О На заседании кафедры прикладная математика Протокол № от
Луганск 2013
УДК 378.147:51
Методические рекомендации к самостоятельной и практической работе по дисциплине "Теория управления" (для студентов специальности "Прикладная математика")/ Составители: Ю.М. Нефедов, Ю.С. Краснобрыжева, Т.Ю. Балицька.. – Луганск: Изд-во ВНУ им. В. Даля, 2013.– 43 с.
В методичних рекомендаціях пропонується послідовність дій для самостійного виконання логіко-дидактичного аналізу теоретичного матеріалу певної теми, а також зразок логіко-дидактичного аналізу теми "Многокутники" (9 клас).
Составители Ю.М. Нефедов, доц., Ю.С. Краснобрыжева, ст.викл., Т.Ю. Балицька, ас.
Ответственный за выпуск В.Я. Кучма, доц.
Рецензент С.А. Митрохин, доц.
Теория управления – раздел науки, посвященный изучению динамических управляемых объектов и определению наилучших способов управления ими. ПОСТАНОВКА ЗАДАЧИ ТЕОРИИ УПРАВЛЕНИЯ Примеры систем управления и их Математические модели Реальные системы управления, как правило, достаточно сложны. Приведенные ниже примеры используются для иллюстрации основных задач теории управления. Поэтому рассматриваемые системы управления отличаются максимальной простотой и наглядностью. Пример 1.1. Предположим, что некоторая материальная точка Пусть известно, что в начальный момент времени
и в течение всего движения этой точки сила
Можно поставить задачу: определить силу
за минимально возможное время
Согласно второму закону Ньютона уравнение движения точки
Точку
Поставленная задача называется задачей о быстродействии. При решении задач управления пользуются фазовыми координатами и фазовым пространством. В данном случае фазовыми координатами являются две переменные
Фазовые координаты дают возможность записать граничные условия (1.2) и (1.4) в виде
а уравнение (1.6) в виде системы двух дифференциальных уравнений первого порядка
Точка Пример 1.2. Рассмотрим материальную точку массы
где Проектируя уравнение (1.9) на горизонтальную и вертикальнуюоси координат, получим следующие уравнения движения:
где
где
где
Пример 1.3. Рассмотрим уравнение простого осциллятора
Обозначая
где Импульсная переходная матрица для этой системы удовлетворяет уравнению
при начальном условии Ряд (1.19) для вычисления
Простое вычисление показывает, что
где использованы разложения тригонометрических функций в ряд Тейлора
Следовательно,
Пример 1.4. Рассмотрим неоднородное дифференциальное уравнение
которое можно представить в виде нормальной системы уравнений
Вычисление переходной матрицы немедленно дает
Используя формулу Коши
получим общее решение системы
Заметим, что несмотря на внешнюю простоту выражения для переходной матрицы в стационарной системе, вычисление функции С помощью импульсной переходной матрицы
Определение. Пусть
или, что то же самое,
Здесь преобразование по Лапласу матрицы понимается как матрица преобразований по Лапласу всех ее элементов. Применяя преобразование Лапласа к равенству (1.20) и учитывая теорему о свертке (произведение изображений)
для (1.22) можем получить соотношение
где
Для решения обыкновенных дифференциальных уравнений широко используется аппарат преобразования Лапласа. Этот аппарат можно непосредственно использовать для вычисления импульсной переходной матрицы следующим образом. Используем принятое обозначение для преобразования Лапласа функции
где Рассмотрим стационарную однородную систему
и ее преобразование Лапласа
Тогда
Матрица
Последовательность вычислений такова: 1. Вычисление обратной матрицы 2. С помощью таблиц обратного преобразования Лапласа (см. Приложение) определение элементов переходной матрицы
Пример 1.5. Пусть система Характеристическая матрица: Вычисляем обратную матрицу. При этом определитель исходной матрицы:
Пользуясь таблицей обратного преобразования Лапласа (см. Приложение), получим
ЛИНЕЙНЫХ СИСТЕМАХ Критерий управляемости В стационарном случае критерий управляемости принимает простую и компактную форму. Пусть заданы матрицы системы
Управляемость стационарной системы (2.1) связанасо свойствами матрицы Лемма 2.1. Если ранг матрицы Доказательство этой леммы можно найти в [4, с.86]. Из этой леммы, в частности, следует, что прибавление каждого последующего элемента вида Сформулируем теперь основной (в смысле управляемости) результат теории линейных стационарных систем. Теорема 2.2. (критерий управляемости стационарной системы). Линейная стационарная п-мерная система (2.1) вполне управляема тогда и только тогда, когда ранг Доказательство. Достаточность. Предположим, что ранг матрицы
Сформулированное утверждение равнозначно следующему: если существует некоторый отрезок Для доказательства последнего утверждения продифференцируем
Учитывая формулу (1.20), можем записать
где Известно [4, с.62], что матрица
а поэтому имеем
или
Используя свойство (2.6), из равенств (2.5) легко получить соотношения
Положив здесь
Это в свою очередь возможно только в том случае, если ранг матрицы Необходимость условий теоремы будет установлена, если докажем, что из линейной независимости вектор-функции (2.2) при Предположим, что ранг матрицы
Учитывая утверждение леммы 2.1, приходим к выводу, что
для всех целых Принимая во внимание, что матрицу
то для линейной комбинации векторов (2.4) получим выражение
Если в этом равенстве за вектор
что означает линейную зависимость векторов (2.2). Замечание. В случае, если вектор управления в системе (2.1) одномерный, матрица
Соотношения (2.3) и (2.10) назовем условиями вполне управляемости стационарных систем. Определение. Система (2.1) называется вполне управляемой на заданном промежутке
Согласно доказанной теореме 2.2 свойство управляемости системы полностью определяется алгебраическими свойствами пары матриц Задача Лагранжа Дано: – функционал – – начальные условия
Требуется найти вектор-функцию Предположим, что система уравнений (3.1) позволяет найти управление
Подставляя вектор
Таким образом, задача оптимизации системы управления заключается в нахождении оптимальной траектории системы из условия минимума функционала (3.7), что полностью совпадает с задачей Лагранжа. Как известно, основными задачами вариационного исчисления, кроме задачи Лагранжа, являются задача Майера и задача Больца. Напомним их постановку в терминах и символах теории систем управления. Задача Майера. Дано: – уравнения движения системы (3.1); – начальное состояние системы(3.2); – конечное состояние системы
– критерий оптимальности
где Требуется определить вектор-функцию Замечание 1. В этой задаче условия (3.8) могут заменяться условиями
Замечание 2. Если в задаче Майера функция Задача Больца Дано: – уравнения движения системы (3.1); – начальное состояние системы (3.2); – конечное состояние системы (3.8) или (3.8*); – критерий оптимальности
где Задача заключается в нахождении функции Формулировка задачи Больца - наиболее общая. Но всегда возможно ввести некоторые дополнительные переменные, преобразующие задачу Лагранжа в задачу Больца или в задачу Майера и наоборот.
На наш взгляд, целесообразно рассмотреть один такой прием, достаточно часто используемый в приложениях. Рассмотрим задачу Лагранжа (3.1), (3.2), (3.3). Введем дополнительную переменную
или, иначе
Присоединяя уравнение (3.12) ксистеме (3.1), а условие (3.13) к начальным условиям (3.2), получим
Итак, задача оптимизации управления сведена к нахождению экстремума критерия
при условиях (3.14) и (3.15), т. е. к задаче Майера. Приведем теперь основные положения вариационного исчисления, используемые для оптимизации систем управления. Экстремума функционалов Основной вопрос вариационного исчисления – вывод необходимых условий экстремума (для определенности – минимума). На управление Рассмотрим линейную управляемую систему:
(некоторые из коэффициентов
и ограничения наложены только на управление Данную задачу о быстродействии сводим, согласно правилу построения функции Лагранжа, к задаче о минимуме линейного функционала
при граничных условиях Необходимым условием экстремума, достигаемого не на границе области, является выполнение системы уравнений Эйлера
Но второе уравнение в (3.43) может выполняться лишь в особом случае, когда
т.е. когда функции Следовательно, за исключением особого случая, экстремалей внутри области не существует. Следовательно, экстремум может достигаться на границе области, где Таким образом, функционал (3.42) на самом деле является функцией от переменных Задачу вариационного исчисления на этом можно считать решенной: мы свели ее к задаче принципиально более простой – задаче на экстремум конечного числа переменных.
Однако на практике отыскать точки разрыва методами дифференциального исчисления нелегко, особенно если учесть, что число их неизвестно. Для их нахождения применим следующий прием: условие
где Действительно, если Для этой изопериметрической задачи функция Лагранжа имеет вид
и в качестве уравнений Эйлера получаем следующую систему уравнений:
Из уравнения (3.47) следует, что
но при Символически это записывается так:
где символ sign означает, что Так доказывается общая теорема о числе переключений от Теорема 3.1. (Об более Эта теорема используется при расчетах оптимального по быстродействию управления для линейных систем, так как позволяет свести вариационную задачу к задаче на экстремум функции
И фиксированным временем Все теоремы принципа максимума относятся к системам, поведение которых можно описать дифференциальными уравнениями:
где Ставится задача – найти управление
Замечаем, что в отличие от обычных задач вариационного исчисления, где все искомые функции были равноправны, в принципе максимума разделяются фазовые координаты и управления. Это разделение удобно в тех случаях, когда ограничения накладываются только на управления, а не на фазовые координаты, например, если задано
Важную роль в принципе максимума играют вспомогательные переменные
При помощи этой функции основная система уравнений (4.1) и уравнения, необходимые для определения вспомогательных переменных
Действительно, так как Теорема 4.1. Для оптимальности управления
Кроме того, в конечный момент времени
|

 массы
массы  может двигаться только по прямой линии, вдоль которой на точку действует сила
может двигаться только по прямой линии, вдоль которой на точку действует сила  . Положение точки
. Положение точки  (рис. 1.1).
(рис. 1.1). выполнены условия
выполнены условия (1.2)
(1.2) . (1.3)
. (1.3)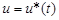 , под действием которой точка
, под действием которой точка  перемещается в другое заданное состояние, например,
перемещается в другое заданное состояние, например, (1.4)
(1.4) . (1.5)
. (1.5) . (1.6)
. (1.6) является управляющим воздействием или управлением.
является управляющим воздействием или управлением.
 и
и  , связанные с переменной
, связанные с переменной  равенствами
равенствами .
. (1.7)
(1.7) (1.8)
(1.8) на плоскости
на плоскости  является фазовой точкой системы (рис. 1.2). С изменением времени
является фазовой точкой системы (рис. 1.2). С изменением времени 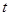 точка
точка  , возникающая в результате отделения от нее частиц с элементарной массой
, возникающая в результате отделения от нее частиц с элементарной массой  . Тогда масса точки является величиной переменной
. Тогда масса точки является величиной переменной  и ее движение можно описать векторным уравнением Мещерского [7, с.25], которое соответствует второму закону Ньютона для точки с переменной массой
и ее движение можно описать векторным уравнением Мещерского [7, с.25], которое соответствует второму закону Ньютона для точки с переменной массой , (1.9)
, (1.9) – вектор абсолютной скорости точки
– вектор абсолютной скорости точки  ,
,  – неизменная часть массы точки,
– неизменная часть массы точки,  – реактивная масса точки;
– реактивная масса точки;  ,
,  – вектор относительной скорости отделяющейся частицы;
– вектор относительной скорости отделяющейся частицы;  – вес.
– вес. (1.10)
(1.10)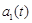 и
и  – проекции вектора
– проекции вектора 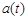 на оси
на оси  и
и  . Допуская, что абсолютная величина вектора
. Допуская, что абсолютная величина вектора  (1.11)
(1.11) ,
,  ,
,  – угол между вектором
– угол между вектором  (рис.1.3). В матричной форме система (1.11) запишется так:
(рис.1.3). В матричной форме система (1.11) запишется так: , (1.12)
, (1.12) .
.
 .
.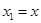 и
и 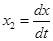 , получим нормальную форму уравнения движения системы в матричном виде:
, получим нормальную форму уравнения движения системы в матричном виде: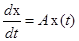 ,
,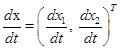 ,
, 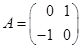 ,
, 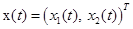 .
.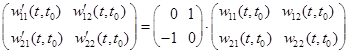
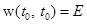 .
.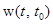 в этом примере легко суммируется потому, что матрица
в этом примере легко суммируется потому, что матрица  – постоянная и, кроме того,
– постоянная и, кроме того, 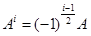 для
для 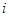 нечетных и
нечетных и 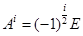 для
для 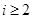 четных. Например,
четных. Например,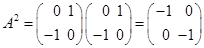 ,
,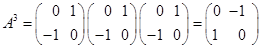 ,
,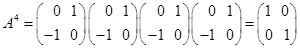 и т.д.
и т.д.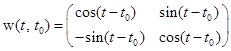 ,
,
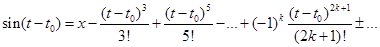
 ,
,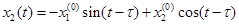 .
. ,
, .
. .
.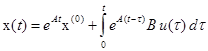
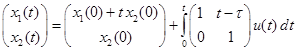 .
.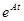 может оказаться сложной задачей.
может оказаться сложной задачей.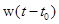 можно записать удобную связь между выходными и входными сигналами системы управления (1.13) при условии, что последняя находится в покое до момента подачи входного сигнала. Эта связь устанавливается в соответствии с результатом теоремы 1.3 и имеет вид
можно записать удобную связь между выходными и входными сигналами системы управления (1.13) при условии, что последняя находится в покое до момента подачи входного сигнала. Эта связь устанавливается в соответствии с результатом теоремы 1.3 и имеет вид . (1.22)
. (1.22)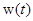 импульсная переходная матрица некоторой системы управления. Если существует преобразование Лапласа матрицы
импульсная переходная матрица некоторой системы управления. Если существует преобразование Лапласа матрицы 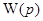 , т. е.
, т. е.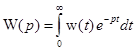 , (1.23)
, (1.23)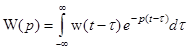 . (1.24)
. (1.24)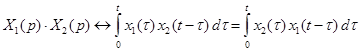 ,
,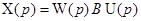 ,
,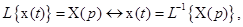
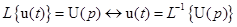 .
. :
: 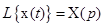 . Тогда, согласно теории этого преобразования, если функция
. Тогда, согласно теории этого преобразования, если функция  ,
,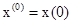 .
.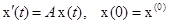
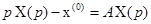 .
.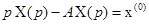 или
или 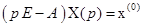 .
.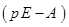 является характеристической матрицей матрицы
является характеристической матрицей матрицы 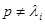 где
где 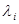 – характеристические числа матрицы
– характеристические числа матрицы 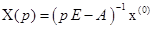 имеет смысл при всех
имеет смысл при всех 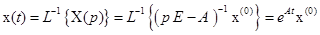 .
.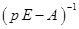 .
.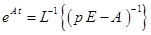 .
.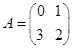 . Построить импульсную переходную матрицу.
. Построить импульсную переходную матрицу.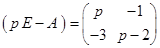 .
.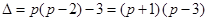 . После несложных преобразований обратная матрица будет иметь следующий вид:
. После несложных преобразований обратная матрица будет иметь следующий вид: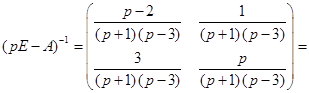
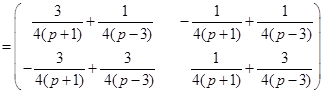 .
.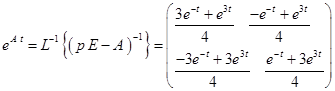 .
. . Составим матрицу
. Составим матрицу 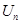 размером
размером  , первые
, первые  столбцов которой совпадают со столбцами матрицы
столбцов которой совпадают со столбцами матрицы  (или просто
(или просто  ) и т. д., последние
) и т. д., последние 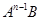 . Матрицу
. Матрицу 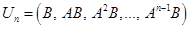 .
. равен рангу матрицы
равен рангу матрицы  , то дальнейшее прибавление столбцов вида
, то дальнейшее прибавление столбцов вида  ,
,  , не увеличивает ранга матрицы.
, не увеличивает ранга матрицы. либо увеличивает ранг матрицы на некоторое постоянное число, либо не меняет ранга. В последнем случае и прибавление всех последующих столбцов вида
либо увеличивает ранг матрицы на некоторое постоянное число, либо не меняет ранга. В последнем случае и прибавление всех последующих столбцов вида  . (2.3)
. (2.3) и покажем, что в этом случае вектор-функции
и покажем, что в этом случае вектор-функции  матрицы
матрицы  при
при  и
и  линейно независимы на произвольном интервале
линейно независимы на произвольном интервале  . Иначе говоря, следует доказать, что, если ранг матрицы
. Иначе говоря, следует доказать, что, если ранг матрицы 
 , что имеет место тождество
, что имеет место тождество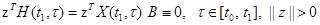 . (2.4)
. (2.4) раз тождество (2.4) по переменной
раз тождество (2.4) по переменной 
 (2.5)
(2.5) ,
, – обратная матрица по отношению к матрице
– обратная матрица по отношению к матрице  фундаментальных решений однородного уравнения для уравнения (2.1).
фундаментальных решений однородного уравнения для уравнения (2.1). удовлетворяет уравнению
удовлетворяет уравнению ,
,
 . (2.6)
. (2.6)
 , имеем
, имеем (2.7)
(2.7) вытекает равенство ранга матрицы
вытекает равенство ранга матрицы  , что
, что . (2.8)
. (2.8) (2.9)
(2.9) .
. можно изобразить степенным рядом
можно изобразить степенным рядом ,
, .
. ,
,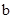 , а поэтому необходимое и достаточное условие вполне управляемости принимает форму
, а поэтому необходимое и достаточное условие вполне управляемости принимает форму . (2.10)
. (2.10) и
и  из фазового пространства
из фазового пространства  можно указать такую функцию управления
можно указать такую функцию управления  , что решение уравнения(1) удовлетворяет краевым условиям
, что решение уравнения(1) удовлетворяет краевым условиям и
и  .
. . Именно, если матрица
. Именно, если матрица  , составленная указанным выше образом, имеет полный ранг, то система управляема.
, составленная указанным выше образом, имеет полный ранг, то система управляема.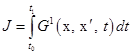 ; (3.4)
; (3.4)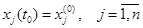 . (3.5)
. (3.5) , обеспечивающую минимум функционалу
, обеспечивающую минимум функционалу 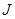 и удовлетворяющую условиям (3.5).
и удовлетворяющую условиям (3.5). в виде
в виде . (3.6)
. (3.6)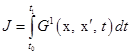 . (3.7)
. (3.7)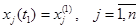 ; (3.8)
; (3.8) , (3.9)
, (3.9) функция, определенная на не полностью заданном множестве конечных состояний системы.
функция, определенная на не полностью заданном множестве конечных состояний системы.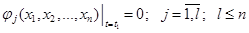 . (3.8*)
. (3.8*) , то она становится задачей о быстродействии.
, то она становится задачей о быстродействии. , (3.10)
, (3.10) и
и  по формуле
по формуле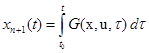 , (3.11)
, (3.11)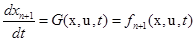 , (3.12)
, (3.12) . (3.13)
. (3.13) , (3.14)
, (3.14)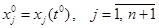 . (3.15)
. (3.15) (3.16)
(3.16)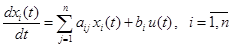 (3.41)
(3.41)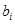 могут быть равны нулю), а функционалом, экстремум которого нам надлежит определить, является время достижения системой положения равновесия, т. е.
могут быть равны нулю), а функционалом, экстремум которого нам надлежит определить, является время достижения системой положения равновесия, т. е.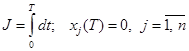 ,
,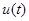 .
.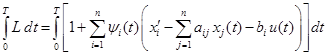 (4.42)
(4.42)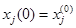 ;
; 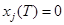 и ограничении по модулю
и ограничении по модулю  .
.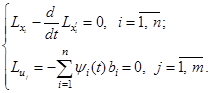 (3.43)
(3.43)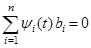 , (3.44)
, (3.44)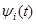 линейно зависимые, т.е. связаны между собой линейным соотношением (3.44).
линейно зависимые, т.е. связаны между собой линейным соотношением (3.44).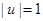 , т. е. либо
, т. е. либо  , либо
, либо 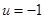 . Поскольку в функцию Лагранжа
. Поскольку в функцию Лагранжа 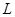 не входят производные
не входят производные 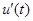 , то, экстремум может достигаться на разрывной функции
, то, экстремум может достигаться на разрывной функции  (рис.3.2).
(рис.3.2).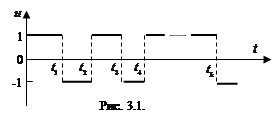
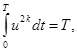 (3.45)
(3.45)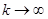 .
.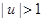 , то
, то 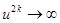 при
при 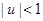 , то
, то  и значение интеграла будет меньше
и значение интеграла будет меньше 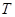 . Поэтому задача об экстремуме функционала (3.42) при условии
. Поэтому задача об экстремуме функционала (3.42) при условии 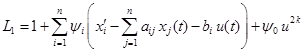 ,
,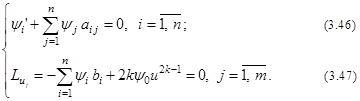
 ,
, из любого числа
из любого числа 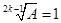 , если
, если 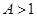 , и
, и  , если
, если  .
. ,
,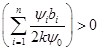 , и
, и 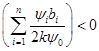 .
. в
в  ), будет содержать не более
), будет содержать не более 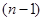 переключений, т.е. не
переключений, т.е. не , (4.1)
, (4.1) в состояние
в состояние  за время
за время  и доставляющее минимум функционалу
и доставляющее минимум функционалу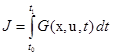 . (4.2)
. (4.2) .
. и промежуточная функция, которая называется функцией Гамильтона (или гамильтонианом):
и промежуточная функция, которая называется функцией Гамильтона (или гамильтонианом): . (4.3)
. (4.3) (4.4)
(4.4) (4.5)
(4.5) , то уравнения (4.4) эквивалентны уравнениям (4.1); в то же время из уравнений (4.5) можно найти вспомогательные переменные
, то уравнения (4.4) эквивалентны уравнениям (4.1); в то же время из уравнений (4.5) можно найти вспомогательные переменные  для того, чтобы быть оптимальным, формулируется в виде теоремы о максимуме:
для того, чтобы быть оптимальным, формулируется в виде теоремы о максимуме: и траектории
и траектории  необходимо существование такой ненулевой непрерывной функции
необходимо существование такой ненулевой непрерывной функции  , удовлетворяющей уравнениям (4.5), что при любом
, удовлетворяющей уравнениям (4.5), что при любом  , кроме точек разрыва
, кроме точек разрыва  достигает максимума, т.е.
достигает максимума, т.е. . (4.6)
. (4.6) выполняются соотношения:
выполняются соотношения:


