
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные виды уравнений плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Аналитическая Геометрия
Практикум
Красноярск СФУ
УДК 514.12(07) ББК 22.151.54я73
Составители: М. Н. Арасланова, Т. П. Мансурова
Аналитическая геометрия: практикум [Текст] / сост. М. Н. Арасланова, Т. П. Мансурова. – Красноярск: Сиб. Федер. Ун-т, 2012. – 64 с.
В практикуме приведены основные теоретические сведения раздела математики «Аналитическая геометрия» и разобраны примеры решения типовых задач. Предназначено для студентов всех специальностей направлений: 130100 Прикладная геология, 130200 Технологии геологической разведки, 130400 Горное дело, 140600 Электротехника, электромеханика и электротехнологии, 150400 технологические машины и оборудование, 150000 Металлургия, машиностроение и металлообработка, 280100 Безопасность жизнедеятельности, 150700 Физическое материаловедение, 080500 Менеджмент.
УДК 514.12(07) ББК 22.151.54я73 ÓСибирский федеральный университет, 2012 ВВЕДЕНИЕ
Значение раздела «аналитическая геометрия» математики определяется тем, что подавляющее большинство прикладных задач носят “линейный” характер, а те, что не являются “линейными”, как правило, допускают “линеаризацию”. Сплав двух важнейших идей - идеи координат и идеи вектора - и лежит в основе учебной дисциплины “линейная алгебра с элементами аналитической геометрии”. Математический аппарат, которым студент овладевает в процессе ее изучения, используется практически во всех приложениях математики. Практикум написан в соответствии с программой данного курса. Содержит элементы аналитической геометрии, теорию определителей, систем линейных уравнений, векторов. Отличается большим количеством типовых примеров.
Уравнение плоскости Взаимное расположение плоскостей
Пусть даны две плоскости A1 x +B1 y +C1 z +D1=0 и A2 x +B2 y +C2 z +D2=0. Любые две пересекающиеся плоскости образуют два угла в сумме равные p. Угол j между нормальными векторами плоскостей
Плоскости параллельны, если векторы
Плоскости перпендикулярны, если векторы
Замечание. Если даны три плоскости своими уравнениями A1 x +B1 y +C1 z +D1=0, A2 x +B2 y +C2 z +D2=0 и A3 x +B3 y +C3 z +D3=0, то их общие точки определяются из системы уравнений, составленной из уравнений плоскостей. В случаях, когда нормальные векторы этих плоскостей
и определитель является определителем системы. Такая система имеет единственное решение. Уравнения прямой в пространстве Одна и та же прямая линия может быть описана различными уравнениями. Кривые второго порядка
Уравнения кривых второго порядка представлены в табл. 2. Таблица 2
Поверхности второго порядка Основные типы поверхностей Классификация поверхностей в пространстве находится в полной аналогии с классификацией линий на плоскости. Определение. Поверхность второго порядка – это множество точек трехмерного пространства, координаты которых в декартовой системе координат удовлетворяет уравнению (описывается в общем случае многочленом второго порядка): Ax 2+ By 2+ Cz 2+ Dxy + Еxz + Fyz + Gx + Hy + Kz + L =0, в котором A 2+ B 2+ C 2+ D 2+ Е 2+ F 2¹ 0. Таблица 3
Метод сечений Сущность метода сечений состоит в том, что рассматриваются линии пересечения данной поверхности с различными плоскостями. Во многих случаях удобно рассекать поверхность плоскостями, параллельными одной из координатных плоскостей, например параллельными плоскости x 0 y. Уравнение одной такой плоскости имеет вид z = h, где h есть некоторое число, которое можно выбирать произвольно. Плоская кривая, получаемая в сечении, представляется системой уравнений, одно из которых z = h, а другое – данное уравнение поверхности. Если в последнее подставить вместо координаты z значение h, то получим уравнение, не содержащее z. Это уравнение позволит построить сечение. Зная ряд сечений, можно получить представление о самой поверхности.
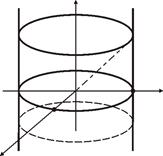
Пример. Построить поверхность z 2= x 2+ y 2, используя метод сечений. Решение. Чтобы получить представление о форме поверхности, будем рассекать ее плоскостями z = h. Линия сечения представляется системой уравнений
Подставив вместо z в первое уравнение h, получим равносильную систему уравнений:
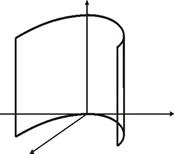
которая представляет окружность радиуса R = h с центром в точке О1(0; 0; h). Значит, линией пересечения плоскости z = h с круглой цилиндрической поверхностью будет окружность. Придавая z = h любое значение, получим ряд окружностей, расположить которые нужно параллельно плоскости x 0 y на расстояниях, равных радиусу h. Если в качестве секущей плоскости взять плоскость x 0 z (y =0), то линия пересечения представится системой
Эта система описывает пару взаимно перпендикулярных прямых (рис. 5, АВ, А1В1), лежащих в плоскости x 0 z:
Таким образом, данная поверхность представляет собой поверхность круглого конуса, у которого образующая составляет с осью угол в 450. Сечения поверхности плоскостями, параллельными плоскости x 0 z (или x 0 y), могут дополнить наши сведения о форме конической поверхности. Так, из системы:
получим равносильную ей систему
т.е. сечение конуса плоскостями, параллельными плоскости x 0 z, есть гиперболы.
Рис. 5 Полярные координаты
Полярная система координат определяется заданием точки О, луча ОР, масштабной единицы l.
Рис. 6 ОР - полярная ось, О - полярный полюс, r – расстояние точки М от полюса О, l – единица масштаба, j - угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ (рис. 6). Эти числа r и j называют полярными координатами точки М, причем величину r – полярным радиусом, а j – полярным углом точки М (0£j<2p, r >0). Если совместить декартову систему координат с полярной (ось ОР пойдет по оси О х, а полюс О совпадет с началом координат), то связь между декартовыми координатами (х, у) каждой точки М и полярными ее координатами (r, j) будет такой: x = r ×cos j, y = r ×sin j, r = Решение типовых задач Задача 1. Даны точки А(-1; 2; -5) и В(-8; -3; -4). Составить уравнение плоскости, проходящей через точку А и перпендикулярной вектору Решение. Найдем координаты нормального вектора
Задача 2. Даны три точки А, В и С. Найти уравнение плоскости, на которой лежат данные точки. 1. A (1,2,3), B (4,-1,-2), C (4,0,3). Решение. Пусть М (x, y, z) – произвольная точка плоскости. Тогда векторы
Вычисляем определитель разложением по элементам первой строки. (x -1)×(-1)1+1× (x -1)×(-3×0-(-2)×(-5))+(y -2)×(-1)×(3×0-3×(-5))+(z -3)×(3×(-2)-3×(-3))=0, (x -1)×(0+10)-(y -2)×(0+15)+(z -3)×(-6+9)=0, 10×(x -1)-15×(y -2)+3×(z -3)=0, 10 x -10-15 y +30+3 z -9=0, 10 x -15 y +3 z +11=0 – искомое уравнение. Ответ: 10 x -15 y +3 z +11=0. 2. A (1,2,0), B (1,-1,2) и C (0,1,-1). Решение. Пусть М (x, y, z) – произвольная точка плоскости. Тогда векторы
Векторы
Вычисляем определитель разложением по элементам первой строки: (x -1)× (x -1)×(3-(-2))-(y -2)×(0-(-2))+ z (0-3)=0, 5 x- 5-2 y +4-3 z =0, 5 x -2 y -3 z -1=0 – искомое уравнение. Ответ: 5 x -2 y -3 z -1=0. Задача 3. Найти расстояние от точки А(1; -2; 3) до плоскости 2 x - y -2 z +5=0. Решение. Подставляем в формулу вычисления расстояния от точки до плоскости:
Ответ: 1. Задача 5. Написать уравнение плоскости, проходящей через точку А(1; -2; 0) и параллельно плоскости 2 x -4 y - z +1=0. Решение. Так как плоскости параллельны, то в качестве нормального вектора можно взять нормальный вектор данной плоскости, т.е. Получаем общее уравнение плоскости 2(x -1)-4(y +2)-(z -0)=0, 2 x -4 y - z -10=0. Задача 6. Составить уравнение плоскости, проходящей через две параллельные прямые Решение. Пусть М (x, y, z) – произвольная точка плоскости. Тогда векторы
Вычисляем определитель разложением по элементам первой строки: (x -3)× (x -3)×(3-12)-(y -2)×(18-6)+(z +1)(-24-(-2))=0, -9(x -3)-12(y -2)-22(z +1)=0, 9 x +12 y +22 z -29=0, Ответ: 9 x +12 y +22 z -29=0. Задача 7. Даны точки А и В. Найти уравнение прямой, проходящей через данные точки. 1. A (-1,2,3), B (2,6,-2). Решение. Составим каноническое уравнение прямой, проходящей через две точки:
(Здесь первой точкой считали А, а второй – В.) 2. A (2,-1,3), B (2,3,3).
Задача 8. Привести к каноническому виду общее уравнения прямой
Решение. Для того, чтобы записать каноническое уравнение искомой прямой достаточно найти: 1) хотя бы одну точку А, через которую проходит данная прямая; 2) ее направляющий вектор В качестве точки А можно принять точку ее пересечения с любой из координатных плоскостей, например, с плоскостью x 0y. Поскольку при этом z 1=0, координаты x 1, y 1 определяются из системы уравнений заданных плоскостей, если положить в них z =0:
Отсюда x 1=2, y 1=4. Направляющий вектор Способ 1. Определить координаты еще одной любой точки прямой, например, В(0; 24; 14). Тогда в качестве вектора
Тогда искомое уравнение прямой запишется в виде
Способ 2. Направляющий вектор
Каноническое уравнение прямой примет вид:
Задача 9. Составить уравнения прямой, проходящей через точку А(-1; 3; 2) и параллельно прямой x =4+5 t, y =7 t, z =8-3 t. Решение. Так как искомая прямая параллельна данной прямой, то в качестве ее направляющего вектора можно взять направляющий вектор
в параметрическом виде:
Задача 10. Найти угол между прямыми
Решение. Первая из прямых описана каноническим уравнением, ее направляющий вектор
Задача 11. Дана точка Р (x 0, y 0, z 0) и плоскость (a): Ax + By + Cz + D =0. Найти уравнение прямой, проходящей через данную точку перпендикулярно данной плоскости. Указание. Нормальный вектор плоскости
1. Р (0,0,0) и (a): 4 x-y +2 z -3=0.
2. Р (2,1,-1) и (a): x-y + z +1=0.
3. P (3,-1,-1), (a): 3 x + y + z -20=0.
4. Р (2,3,1), (a): 2 x -3 z +1=0.
Задача 12. Даны уравнения прямой l и плоскости a. Найти угол между ними. Находится по формуле: sin j= 1. Уравнение прямой l: Решение. Направляющий вектор прямой
Находим длины векторов:
sin j= = Ðj=arcsin Ответ: 60049’. 2. Уравнение прямой l: Решение. Направляющий вектор прямой
sin j= = Ðj=arcsin Ответ: 1907’. Задача 13. Найти точку пересечения прямой Решение. Запишем уравнение прямой в параметрической форме:
Подставляя значения x, y, z в уравнение плоскости, имеем 3(2 t -1)-2(t +2)+(- t +1)=0, откуда t =3. Подставим найденное значение t в параметрические уравнения прямой, находим координаты точки пересечения: х =5, y =5, z =-2. Задача 14. Записать уравнение плоскости, проходящей через точку А(1; -2; 3) и прямую Решение. Проверим, лежит ли заданная точка А на прямой
Так как пропорции не выполнены, то точка А не принадлежит данной прямой. Точка В(3; -1; 7) лежит на данной прямой, а направляющий вектор
-13(x -3)+2(y +1)+6(z -7)=0, 13 x -2 y -6 z +1=0. Задача 15. Даны три точки: А (-1,7), В (0,9), С (1,3). Составить уравнение прямой, проходящей через точку А, параллельно прямой ВС. А Î l, l || BC. Решение. Так как Если точка А (-1,7)Î l, есть вектор
Ответ: Задача 16. В D АВС А (0,7), В (2,5), С (6,-4). Составить уравнение медианы, проведенной из вершины С. (рис. 7).
Рис. 7 Решение. Так как М – середина АВ (l=1),
М (1,6)Î(СМ). С (6,-4)Î(СМ), тогда
Ответ: Задача 17. Найти угловые коэффициенты прямых:
l 1: 3 x +5 y -7=0, l 2: 2 x + y =0, l 3: 3 x +2 y +6=0, l 4: 5 x + y -3=0, l 5: 4 x -9 y =0, l 6: 2 y +3=0. Решение. Прямые заданы общими уравнениями. Разрешив каждое относительно у, получим уравнения вида y = k×x + b, из которых и запишем значения k. l 1: 5 y =-3 x +7½:5; y = l 2: y =-2 x, k 2=-2; l 3: 2 y =-3 x -6½:2; y = l 4: y =-5 x +3; k 4=-5; l 5: 9 y =4 x, y = l 6: 2 y =-3, y = Задача 18. Составить уравнения прямой: 1) проходящей через точку (-1,-1) и имеющей угловой коэффициент k =1; 2) проходящей через точку (2,0) и имеющей угловой коэффициент k =-2. Решение. 1) Подставим данные: y -(-1)=1×(x -(-1)), y +1=1×(x +1), y +1= x +1, x - y =0; 2) y -0=-2×(x -2), y =-2 x +2, 2 x + y -2=0. Ответ: х-y =0, 2 x+y -2=0. Задача 10. Найти точку пересечения прямых 3 x -4 y +11=0 и 4 x-y -7=0. Решение. Для этого необходимо решить систему уравнений этих прямых.
Умножим обе части второго уравнения на (-4) и почленно сложим уравнения.
Подставляем х =3 в первое уравнение системы: 3×3-4 y =-11, -4 y =-11-9, -4 y =-20, y =5. Ответ: (3; 5). Задача 19. Даны уравнения сторон треугольника: х +3 у -3=0, 3 х -11 у -29=0 и 3 х-у +11=0. Найти вершины этого треугольника. Решение. Для вычисления координат вершин треугольника необходимо решить три системы уравнений:
Решаем первую систему. Умножаем обе части первого уравнения на (-3):
почленное сложение даст уравнение -20 у -20=0, -20 у =20, у =-1. Система примет вид
находим х, подставляя в первое уравнение найденное значение у: х +3×(-1)-3=0, х -3-3=0, х =6. Одна из вершин (6;-1). Решаем вторую систему. Умножив обе части второго уравнения на (-1) и сложив почленно, получим
Подставляя найденное значение у = – 4 в первое уравнение системы, найдем х: 3× x -11×(-4)-29=0, 3 x =-44+25, 3 x =-15, x =-5. Вторая вершина (-5; -4). Решение третьей системы уравнений:
Подставляя найденное значение х =-3 в первое уравнение системы, найдем у: -3+3 y -3=0, 3 y =6, y =2. Третья вершина (-3;2). Задача 20. Найти угол между двумя прямыми: 1) у =-2 х и у =3 х +5; 2) 4 х +2 у -5=0 и 6 х+ 3 у +1=0; 3) 4) 2 х+ 3 у-1 =0 и 3 х -2 у+ 1=0; 5) 3 х +4 у -5=0 и 5 х -2 у+ 7=0; 6) у =2 х+ 3 и у -4=0. Решение. Находим угловые коэффициенты прямых. А затем находим тангенсы искомых углов. 1) k 1=-2, k 2=3, тогда получим:
2) k 1=-2, k 2=-2, тогда
т.е. данные прямые параллельны; 3) k 1=
4) k 1= Видно, что k 1× k 2=-1; значит, эти две прямые образуют угол 900, т.е. они взаимно перпендикулярны; 5) оба уравнения решим относительно у. Получим уравнения у=
= 6) k 1=2, k 2=0, следовательно,
Задача 21. В D АВС А (4; 6), В (-3; 0), С (2; -3). Найти углы треугольника и уравнение высоты СЕ. Решение. Уравнения прямых (АВ), (ВС) и (СА) найдем, как уравнение прямых, проходящих через 2 точки и сразу же находим угловые коэффициенты. (АВ):
-6 x +24=-7 y +42, 7 y =6 x +42-24, 7 y =6 x +18, y = (BC):
-3 x- 9=5 y, y = (AC):
-9 x +36=-2 y +12, 2 y =9 x -24, y = Теперь находим углы треугольника:
tg C = Получили, что Ð В =Ð С» 71034’, т.е. D АВС – равнобедренный. Найдем уравнение высоты (СЕ). Так как (СЕ)^(АВ), то kСЕ = Значит y -(-3)= 6 y +18=-7 x +14, 7 x +6 y +4=0. Ответ. Ð A»36052’; Ð В =Ð С»71034’; 7 x +6 y+ 4=0. Задача 22. Составить уравнение прямой, проходящей через точку М (-2,4) параллельно прямой 2 х -3 у +6=0. Решение. Так как прямые параллельны, то k 1= k 2. Находим угловой коэффициент данной прямой 3 y =2 x +6 |:3, y = Искомая прямая проходит через точку М (-2,4) и имеет угловой коэффициент k 2= y- 4= 3 y- 12=2 x+ 4, 2 x -3 y +16=0. Ответ. 2 x- 3 y +16=0. Задача 23. Составить уравнение прямой, проходящей через точку М (2,3) перпендикулярно прямой 5 х -4 у -20=0. Решение. Так как прямые перпендикулярны, то 4 у =5 х- 20 |:4, y = тогда угловой коэффициент искомой прямой k 2= Итак, k 2=
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.45.133 (0.014 с.) |

 и
и  равен одному из этих углов и может быть найден по формуле:
равен одному из этих углов и может быть найден по формуле: .
. и
и  коллинеарны, т.е.
коллинеарны, т.е. .
. .
. не компланарны, три плоскости имеют единственную общую точку. Тогда их смешанное произведение
не компланарны, три плоскости имеют единственную общую точку. Тогда их смешанное произведение




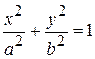






















 .
.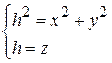 ,
, или
или  .
. .
.
 ,
,

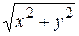 , tg j=
, tg j= 
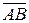 .
. =
=  . Пусть М (x, y, z) – произвольная точка плоскости. Тогда векторы
. Пусть М (x, y, z) – произвольная точка плоскости. Тогда векторы  и
и  ортогональны,т.е. их скалярное произведение равно нулю
ортогональны,т.е. их скалярное произведение равно нулю  , т.е.
, т.е. ,
, .
. ={4-1,0-2,3-3}={3,-2,0} компланарны, поэтому
={4-1,0-2,3-3}={3,-2,0} компланарны, поэтому , то есть
, то есть  .
.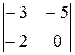 +(y -2)×(-1)1+2×
+(y -2)×(-1)1+2× 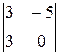 +(z -3)×(-1)1+3×
+(z -3)×(-1)1+3×  =0.
=0.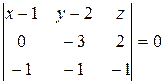 .
. -(y -2)×
-(y -2)× 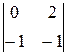 + z ×
+ z ×  =0.
=0. .
. .
. и
и  .
. компланарны, т.е. их смешанное произведение равно нулю
компланарны, т.е. их смешанное произведение равно нулю  , т.е.
, т.е. ,
,  ,
, -(y -2)×
-(y -2)×  +(z+ 1)×
+(z+ 1)×  =0.
=0. ,
,  .
. ;
;  .
. .
. .
. .
. .
. ,
,  , и в качестве вектора
, и в качестве вектора  =
=  .
. .
. данной прямой. Используя уравнение прямой, проходящей через А и параллельной вектору
данной прямой. Используя уравнение прямой, проходящей через А и параллельной вектору  ,
, .
. и
и  .
. . Вторая прямая задана в параметрической форме, ее направляющий вектор
. Вторая прямая задана в параметрической форме, ее направляющий вектор  . Угол между прямыми:
. Угол между прямыми: . Ðj=
. Ðj=  .
. ={ A,B,C } будучи перпендикулярным к данной плоскости параллелен искомой прямой. И его можно считать направляющим вектором этой прямой.
={ A,B,C } будучи перпендикулярным к данной плоскости параллелен искомой прямой. И его можно считать направляющим вектором этой прямой. .
. ;
;  - искомое уравнение.
- искомое уравнение. ;
;  - искомое уравнение.
- искомое уравнение. ;
;  - искомое уравнение.
- искомое уравнение. - искомое уравнение.
- искомое уравнение. .
. , уравнение плоскости a: 2 x - y + z +3=0.
, уравнение плоскости a: 2 x - y + z +3=0. =2×2+(-3)×(-1)+1×1=4+3+1=8.
=2×2+(-3)×(-1)+1×1=4+3+1=8. ,
, .
. =
=  =
=  =
=  =
= =
=  =
=  =
= 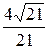 »0,8730.
»0,8730. , уравнение плоскости a: x+2y-z+3 =0.
, уравнение плоскости a: x+2y-z+3 =0. ,
, .
. =
=  =
=  =
= 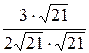 =
=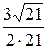 =
=  =
=  »0,3274.
»0,3274. с плоскостью 3 x -2 y + z -3=0.
с плоскостью 3 x -2 y + z -3=0.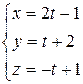 .
. .
. .
. ={ x -3; y +1; z -7},
={ x -3; y +1; z -7}, 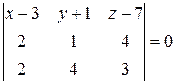 ,
, ,
, || l, то
|| l, то  ,
,  ,
, ,
, 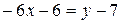 ,
,  .
.
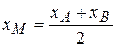 =
=  =1;
=1;  =
=  =
=  =6.
=6. ,
,  ,
,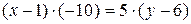 ½:5,
½:5, ,
,  ,
, 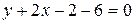 ,
,  .
. , y =
, y =  , k 2=
, k 2= 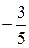 ;
; , y =
, y =  ; k 3=
; k 3= 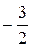 ;
; , y =
, y =  , k 5=
, k 5=  ;
; , k 6=0.
, k 6=0. ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, 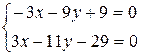 ,
, ,
, ,
,  ,
,  .
. ,
,  ,
,  ,
, ,
,  .
. х-у -2=0 и
х-у -2=0 и  =-1, Ðj=1350;
=-1, Ðj=1350; =0, Ðj=00,
=0, Ðj=00, , k 2=-
, k 2=-  =
=  =
=  =
=  , k 2=
, k 2=  , k 1=
, k 1=  ; y =
; y =  , k 2=
, k 2=  .
. =
=  =
=  =
= =
= 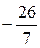 »-3,714, Ðj»10504’;
»-3,714, Ðj»10504’; =
=  =-2, Ðj»116034’.
=-2, Ðj»116034’. ,
, 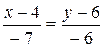 , (x -4)×(-6)=(y -6)×(-7),
, (x -4)×(-6)=(y -6)×(-7), , kAB =
, kAB =  ;
; ,
,  , (x +3)×(-3)= y ×5,
, (x +3)×(-3)= y ×5, , kBC =
, kBC =  ,
,  , (x -4)×(-9)=(y -6)×(-2),
, (x -4)×(-9)=(y -6)×(-2), , kAC =
, kAC =  .
.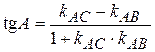 =
=  =
=  =0,75, Ð A»36052’;
=0,75, Ð A»36052’; =
=  =3, Ð B»71034’;
=3, Ð B»71034’; =3, Ð C»71034’.
=3, Ð C»71034’. =
=  , и точка С (2,-3) лежит на (СЕ).
, и точка С (2,-3) лежит на (СЕ). , y +3=
, y +3=  |×6, 6 y +18=-7(x- 2),
|×6, 6 y +18=-7(x- 2), , k 1=
, k 1= 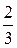 .
. , y -4=
, y -4=  |×3, 3 y -12=2(x +2),
|×3, 3 y -12=2(x +2), . Находим угловой коэффициент данной прямой:
. Находим угловой коэффициент данной прямой: , k 1=
, k 1=  ,
, .
. и точка М (2,3) лежит на прямой. Уравнение для этой прямой записы
и точка М (2,3) лежит на прямой. Уравнение для этой прямой записы 


