
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения прямой на плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Различные уравнения прямой на плоскости Уравнения прямой на плоскости представлены в табл. 1. Таблица 1.
Общее уравнение прямой называется полным, если все его коэффициенты A, B и C отличны от нуля. Если хотя бы один из них равен нулю, то уравнение называется неполным. Рассмотрим все возможные виды неполных уравнений: 1) C = 0 Û O Î L; 2) A = 0 Û L || O x; 3) B = 0 Û L || Oy; 4) A = C = 0 Û L º Ox; 5) B = C = 0 Û L º Oy.
Рис. 4 Взаимное расположение прямых на плоскости Пусть даны две прямые, заданные общими или каноническими уравнениями, уравнениями с угловыми коэффициентами. Углом q между прямыми называется наименьший из двух смежных углов, образованных этими прямыми. Для прямых, заданных уравнениями с угловыми коэффициентами, тангенс угла между прямыми находится по формуле:
Если прямые заданы общими или каноническими уравнениями, то задача об определении угла между прямыми сводится к определению угла между нормальными или направляющими векторами:
Рассмотрим условия параллельности и перпендикулярности прямых. Если прямые заданы уравнениями с угловыми коэффициентами: l 1: y = k 1× x + b, l 2: y = k 2 ×x+b, то l 1 êê l 2 Û k 1= k 2 l 1 ^ l 2 Û k 1× k 2=-1 или Если прямые заданы общими уравнениями: l 1: A 1 x + B 1 y+C =0, l 2: A 2 x + B 2 y+C =0, то l 1 êê l 2 Û l 1 ^ l 2 Û Если прямые заданы каноническими уравнениями: l 1: l 1 êê l 2 Û l 1 ^ l 2 Û Кривые второго порядка
Уравнения кривых второго порядка представлены в табл. 2. Таблица 2
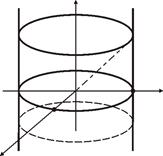
Поверхности второго порядка Основные типы поверхностей Классификация поверхностей в пространстве находится в полной аналогии с классификацией линий на плоскости. Определение. Поверхность второго порядка – это множество точек трехмерного пространства, координаты которых в декартовой системе координат удовлетворяет уравнению (описывается в общем случае многочленом второго порядка): Ax 2+ By 2+ Cz 2+ Dxy + Еxz + Fyz + Gx + Hy + Kz + L =0, в котором A 2+ B 2+ C 2+ D 2+ Е 2+ F 2¹ 0. Таблица 3
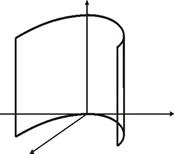
Метод сечений Сущность метода сечений состоит в том, что рассматриваются линии пересечения данной поверхности с различными плоскостями. Во многих случаях удобно рассекать поверхность плоскостями, параллельными одной из координатных плоскостей, например параллельными плоскости x 0 y. Уравнение одной такой плоскости имеет вид z = h, где h есть некоторое число, которое можно выбирать произвольно. Плоская кривая, получаемая в сечении, представляется системой уравнений, одно из которых z = h, а другое – данное уравнение поверхности. Если в последнее подставить вместо координаты z значение h, то получим уравнение, не содержащее z. Это уравнение позволит построить сечение. Зная ряд сечений, можно получить представление о самой поверхности. Пример. Построить поверхность z 2= x 2+ y 2, используя метод сечений. Решение. Чтобы получить представление о форме поверхности, будем рассекать ее плоскостями z = h. Линия сечения представляется системой уравнений
Подставив вместо z в первое уравнение h, получим равносильную систему уравнений:
которая представляет окружность радиуса R = h с центром в точке О1(0; 0; h). Значит, линией пересечения плоскости z = h с круглой цилиндрической поверхностью будет окружность. Придавая z = h любое значение, получим ряд окружностей, расположить которые нужно параллельно плоскости x 0 y на расстояниях, равных радиусу h. Если в качестве секущей плоскости взять плоскость x 0 z (y =0), то линия пересечения представится системой
Эта система описывает пару взаимно перпендикулярных прямых (рис. 5, АВ, А1В1), лежащих в плоскости x 0 z:
Таким образом, данная поверхность представляет собой поверхность круглого конуса, у которого образующая составляет с осью угол в 450. Сечения поверхности плоскостями, параллельными плоскости x 0 z (или x 0 y), могут дополнить наши сведения о форме конической поверхности. Так, из системы:
получим равносильную ей систему
т.е. сечение конуса плоскостями, параллельными плоскости x 0 z, есть гиперболы.
Рис. 5 Полярные координаты
Полярная система координат определяется заданием точки О, луча ОР, масштабной единицы l.
Рис. 6 ОР - полярная ось, О - полярный полюс, r – расстояние точки М от полюса О, l – единица масштаба, j - угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ (рис. 6). Эти числа r и j называют полярными координатами точки М, причем величину r – полярным радиусом, а j – полярным углом точки М (0£j<2p, r >0). Если совместить декартову систему координат с полярной (ось ОР пойдет по оси О х, а полюс О совпадет с началом координат), то связь между декартовыми координатами (х, у) каждой точки М и полярными ее координатами (r, j) будет такой: x = r ×cos j, y = r ×sin j, r = Решение типовых задач Задача 1. Даны точки А(-1; 2; -5) и В(-8; -3; -4). Составить уравнение плоскости, проходящей через точку А и перпендикулярной вектору Решение. Найдем координаты нормального вектора
Задача 2. Даны три точки А, В и С. Найти уравнение плоскости, на которой лежат данные точки. 1. A (1,2,3), B (4,-1,-2), C (4,0,3). Решение. Пусть М (x, y, z) – произвольная точка плоскости. Тогда векторы
Вычисляем определитель разложением по элементам первой строки. (x -1)×(-1)1+1× (x -1)×(-3×0-(-2)×(-5))+(y -2)×(-1)×(3×0-3×(-5))+(z -3)×(3×(-2)-3×(-3))=0, (x -1)×(0+10)-(y -2)×(0+15)+(z -3)×(-6+9)=0, 10×(x -1)-15×(y -2)+3×(z -3)=0, 10 x -10-15 y +30+3 z -9=0, 10 x -15 y +3 z +11=0 – искомое уравнение. Ответ: 10 x -15 y +3 z +11=0. 2. A (1,2,0), B (1,-1,2) и C (0,1,-1). Решение. Пусть М (x, y, z) – произвольная точка плоскости. Тогда векторы
Векторы
Вычисляем определитель разложением по элементам первой строки: (x -1)× (x -1)×(3-(-2))-(y -2)×(0-(-2))+ z (0-3)=0, 5 x- 5-2 y +4-3 z =0, 5 x -2 y -3 z -1=0 – искомое уравнение. Ответ: 5 x -2 y -3 z -1=0. Задача 3. Найти расстояние от точки А(1; -2; 3) до плоскости 2 x - y -2 z +5=0. Решение. Подставляем в формулу вычисления расстояния от точки до плоскости:
Ответ: 1. Задача 5. Написать уравнение плоскости, проходящей через точку А(1; -2; 0) и параллельно плоскости 2 x -4 y - z +1=0. Решение. Так как плоскости параллельны, то в качестве нормального вектора можно взять нормальный вектор данной плоскости, т.е. Получаем общее уравнение плоскости 2(x -1)-4(y +2)-(z -0)=0, 2 x -4 y - z -10=0. Задача 6. Составить уравнение плоскости, проходящей через две параллельные прямые Решение. Пусть М (x, y, z) – произвольная точка плоскости. Тогда векторы
Вычисляем определитель разложением по элементам первой строки: (x -3)× (x -3)×(3-12)-(y -2)×(18-6)+(z +1)(-24-(-2))=0, -9(x -3)-12(y -2)-22(z +1)=0, 9 x +12 y +22 z -29=0, Ответ: 9 x +12 y +22 z -29=0. Задача 7. Даны точки А и В. Найти уравнение прямой, проходящей через данные точки. 1. A (-1,2,3), B (2,6,-2). Решение. Составим каноническое уравнение прямой, проходящей через две точки:
(Здесь первой точкой считали А, а второй – В.) 2. A (2,-1,3), B (2,3,3).
Задача 8. Привести к каноническому виду общее уравнения прямой
Решение. Для того, чтобы записать каноническое уравнение искомой прямой достаточно найти: 1) хотя бы одну точку А, через которую проходит данная прямая; 2) ее направляющий вектор В качестве точки А можно принять точку ее пересечения с любой из координатных плоскостей, например, с плоскостью x 0y. Поскольку при этом z 1=0, координаты x 1, y 1 определяются из системы уравнений заданных плоскостей, если положить в них z =0:
Отсюда x 1=2, y 1=4. Направляющий вектор Способ 1. Определить координаты еще одной любой точки прямой, например, В(0; 24; 14). Тогда в качестве вектора
Тогда искомое уравнение прямой запишется в виде
Способ 2. Направляющий вектор
Каноническое уравнение прямой примет вид:
Задача 9. Составить уравнения прямой, проходящей через точку А(-1; 3; 2) и параллельно прямой x =4+5 t, y =7 t, z =8-3 t. Решение. Так как искомая прямая параллельна данной прямой, то в качестве ее направляющего вектора можно взять направляющий вектор
в параметрическом виде:
Задача 10. Найти угол между прямыми
Решение. Первая из прямых описана каноническим уравнением, ее направляющий вектор
Задача 11. Дана точка Р (x 0, y 0, z 0) и плоскость (a): Ax + By + Cz + D =0. Найти уравнение прямой, проходящей через данную точку перпендикулярно данной плоскости. Указание. Нормальный вектор плоскости
1. Р (0,0,0) и (a): 4 x-y +2 z -3=0.
2. Р (2,1,-1) и (a): x-y + z +1=0.
3. P (3,-1,-1), (a): 3 x + y + z -20=0.
4. Р (2,3,1), (a): 2 x -3 z +1=0.
Задача 12. Даны уравнения прямой l и плоскости a. Найти угол между ними. Находится по формуле: sin j= 1. Уравнение прямой l: Решение. Направляющий вектор прямой
Находим длины векторов:
sin j= = Ðj=arcsin Ответ: 60049’. 2. Уравнение прямой l: Решение. Направляющий вектор прямой
sin j= = Ðj=arcsin Ответ: 1907’. Задача 13. Найти точку пересечения прямой Решение. Запишем уравнение прямой в параметрической форме:
Подставляя значения x, y, z в уравнение плоскости, имеем 3(2 t -1)-2(t +2)+(- t +1)=0, откуда t =3. Подставим найденное значение t в параметрические уравнения прямой, находим координаты точки пересечения: х =5, y =5, z =-2. Задача 14. Записать уравнение плоскости, проходящей через точку А(1; -2; 3) и прямую Решение. Проверим, лежит ли заданная точка А на прямой
Так как пропорции не выполнены, то точка А не принадлежит данной прямой. Точка В(3; -1; 7) лежит на данной прямой, а направляющий вектор
-13(x -3)+2(y +1)+6(z -7)=0, 13 x -2 y -6 z +1=0. Задача 15. Даны три точки: А (-1,7), В (0,9), С (1,3). Составить уравнение прямой, проходящей через точку А, параллельно прямой ВС. А Î l, l || BC. Решение. Так как Если точка А (-1,7)Î l, есть вектор
Ответ: Задача 16. В D АВС А (0,7), В (2,5), С (6,-4). Составить уравнение медианы, проведенной из вершины С. (рис. 7).
Рис. 7 Решение. Так как М – середина АВ (l=1),
М (1,6)Î(СМ). С (6,-4)Î(СМ), тогда
Ответ: Задача 17. Найти угловые коэффициенты прямых: l 1: 3 x +5 y -7=0, l 2: 2 x + y =0, l 3: 3 x +2 y +6=0, l 4: 5 x + y -3=0, l 5: 4 x -9 y =0, l 6: 2 y +3=0. Решение. Прямые заданы общими уравнениями. Разрешив каждое относительно у, получим уравнения вида y = k×x + b, из которых и запишем значения k. l 1: 5 y =-3 x +7½:5; y = l 2: y =-2 x, k 2=-2; l 3: 2 y =-3 x -6½:2; y = l 4: y =-5 x +3; k 4=-5; l 5: 9 y =4 x, y = l 6: 2 y =-3, y = Задача 18. Составить уравнения прямой: 1) проходящей через точку (-1,-1) и имеющей угловой коэффициент k =1; 2) проходящей через точку (2,0) и имеющей угловой коэффициент k =-2. Решение. 1) Подставим данные: y -(-1)=1×(x -(-1)), y +1=1×(x +1), y +1= x +1, x - y =0; 2) y -0=-2×(x -2), y =-2 x +2, 2 x + y -2=0. Ответ: х-y =0, 2 x+y -2=0. Задача 10. Найти точку пересечения прямых 3 x -4 y +11=0 и 4 x-y -7=0. Решение. Для этого необходимо решить систему уравнений этих прямых.
Умножим обе части второго уравнения на (-4) и почленно сложим уравнения.
Подставляем х =3 в первое уравнение системы: 3×3-4 y =-11, -4 y =-11-9, -4 y =-20, y =5. Ответ: (3; 5). Задача 19. Даны уравнения сторон треугольника: х +3 у -3=0, 3 х -11 у -29=0 и 3 х-у +11=0. Найти вершины этого треугольника. Решение. Для вычисления координат вершин треугольника необходимо решить три системы уравнений:
Решаем первую систему. Умножаем обе части первого уравнения на (-3):
почленное сложение даст уравнение -20 у -20=0, -20 у =20, у =-1. Система примет вид
находим х, подставляя в первое уравнение найденное значение у: х +3×(-1)-3=0, х -3-3=0, х =6. Одна из вершин (6;-1). Решаем вторую систему. Умножив обе части второго уравнения на (-1) и сложив почленно, получим
Подставляя найденное значение у = – 4 в первое уравнение системы, найдем х: 3× x -11×(-4)-29=0, 3 x =-44+25, 3 x =-15, x =-5. Вторая вершина (-5; -4). Решение третьей системы уравнений:
Подставляя найденное значение х =-3 в первое уравнение системы, найдем у: -3+3 y -3=0, 3 y =6, y =2. Третья вершина (-3;2). Задача 20. Найти угол между двумя прямыми: 1) у =-2 х и у =3 х +5; 2) 4 х +2 у -5=0 и 6 х+ 3 у +1=0; 3) 4) 2 х+ 3 у-1 =0 и 3 х -2 у+ 1=0; 5) 3 х +4 у -5=0 и 5 х -2 у+ 7=0; 6) у =2 х+ 3 и у -4=0. Решение. Находим угловые коэффициенты прямых. А затем находим тангенсы искомых углов. 1) k 1=-2, k 2=3, тогда получим:
2) k 1=-2, k 2=-2, тогда
т.е. данные прямые параллельны; 3) k 1=
4) k 1= Видно, что k 1× k 2=-1; значит, эти две прямые образуют угол 900, т.е. они взаимно перпендикулярны; 5) оба уравнения решим относительно у. Получим уравнения у=
= 6) k 1=2, k 2=0, следовательно,
Задача 21. В D АВС А (4; 6), В (-3; 0), С (2; -3). Найти углы треугольника и уравнение высоты СЕ. Решение. Уравнения прямых (АВ), (ВС) и (СА) найдем, как уравнение прямых, проходящих через 2 точки и сразу же находим угловые коэффициенты. (АВ):
-6 x +24=-7 y +42, 7 y =6 x +42-24, 7 y =6 x +18, y = (BC):
-3 x- 9=5 y, y = (AC):
-9 x +36=-2 y +12, 2 y =9 x -24, y = Теперь находим углы треугольника:
tg C = Получили, что Ð В =Ð С» 71034’, т.е. D АВС – равнобедренный. Найдем уравнение высоты (СЕ). Так как (СЕ)^(АВ), то kСЕ = Значит y -(-3)= 6 y +18=-7 x +14, 7 x +6 y +4=0. Ответ. Ð A»36052’; Ð В =Ð С»71034’; 7 x +6 y+ 4=0. Задача 22. Составить уравнение прямой, проходящей через точку М (-2,4) параллельно прямой 2 х -3 у +6=0. Решение. Так как прямые параллельны, то k 1= k 2. Находим угловой коэффициент данной прямой 3 y =2 x +6 |:3, y = Искомая прямая проходит через точку
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 748; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.011 с.) |


 , где
, где  – нормальный вектор прямой
– нормальный вектор прямой



 =(l; m), где
=(l; m), где  – направляющий вектор прямой
– направляющий вектор прямой


 .
.

 .
. çç
çç  Û
Û 
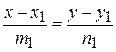 , l 2:
, l 2:  , то
, то çç
çç  Û
Û 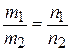




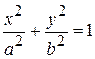






















 .
.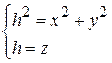 ,
, или
или  .
. .
.
 ,
,

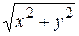 , tg j=
, tg j= 
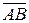 .
. =
=  . Пусть М (x, y, z) – произвольная точка плоскости. Тогда векторы
. Пусть М (x, y, z) – произвольная точка плоскости. Тогда векторы  и
и  ортогональны,т.е. их скалярное произведение равно нулю
ортогональны,т.е. их скалярное произведение равно нулю  , т.е.
, т.е. ,
, .
. ={4-1,0-2,3-3}={3,-2,0} компланарны, поэтому
={4-1,0-2,3-3}={3,-2,0} компланарны, поэтому , то есть
, то есть  .
.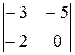 +(y -2)×(-1)1+2×
+(y -2)×(-1)1+2× 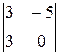 +(z -3)×(-1)1+3×
+(z -3)×(-1)1+3×  =0.
=0.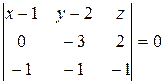 .
. -(y -2)×
-(y -2)× 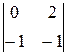 + z ×
+ z ×  =0.
=0. .
. .
. и
и  .
. , т.е.
, т.е. ,
,  ,
, -(y -2)×
-(y -2)×  +(z+ 1)×
+(z+ 1)×  =0.
=0. ,
,  .
. ;
;  .
. .
. .
. .
. .
. ,
,  , и в качестве вектора
, и в качестве вектора  и
и  =
=  .
. .
. данной прямой. Используя уравнение прямой, проходящей через А и параллельной вектору
данной прямой. Используя уравнение прямой, проходящей через А и параллельной вектору  ,
, .
. и
и  .
. . Вторая прямая задана в параметрической форме, ее направляющий вектор
. Вторая прямая задана в параметрической форме, ее направляющий вектор  . Угол между прямыми:
. Угол между прямыми: . Ðj=
. Ðj=  .
. .
. ;
;  - искомое уравнение.
- искомое уравнение. ;
;  - искомое уравнение.
- искомое уравнение. ;
;  - искомое уравнение.
- искомое уравнение. - искомое уравнение.
- искомое уравнение. .
. , уравнение плоскости a: 2 x - y + z +3=0.
, уравнение плоскости a: 2 x - y + z +3=0. =2×2+(-3)×(-1)+1×1=4+3+1=8.
=2×2+(-3)×(-1)+1×1=4+3+1=8. ,
, .
. =
=  =
=  =
=  =
= =
=  =
=  =
= 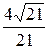 »0,8730.
»0,8730. , уравнение плоскости a: x+2y-z+3 =0.
, уравнение плоскости a: x+2y-z+3 =0. ,
, .
. =
=  =
=  =
= 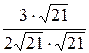 =
=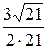 =
=  =
=  »0,3274.
»0,3274. с плоскостью 3 x -2 y + z -3=0.
с плоскостью 3 x -2 y + z -3=0.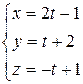 .
. .
. .
. ={ x -3; y +1; z -7},
={ x -3; y +1; z -7}, 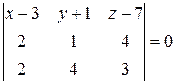 ,
, ,
, || l, то
|| l, то  ,
,  ,
, ,
, 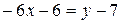 ,
,  .
.
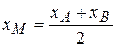 =
=  =1;
=1;  =
=  =
=  =6.
=6. ,
,  ,
,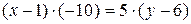 ½:5,
½:5, ,
,  ,
, 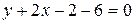 ,
,  .
. , y =
, y =  , k 2=
, k 2= 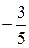 ;
; , y =
, y =  ; k 3=
; k 3= 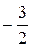 ;
; , y =
, y =  , k 5=
, k 5=  ;
; , k 6=0.
, k 6=0. ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, 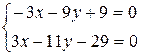 ,
, ,
, ,
,  ,
,  .
. ,
,  ,
,  ,
, ,
,  .
. х-у -2=0 и
х-у -2=0 и  =-1, Ðj=1350;
=-1, Ðj=1350; =0, Ðj=00,
=0, Ðj=00, , k 2=-
, k 2=-  =
=  =
=  =
=  , k 2=
, k 2=  , k 1=
, k 1=  ; y =
; y =  , k 2=
, k 2=  .
. =
=  =
=  =
= =
= 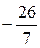 »-3,714, Ðj»10504’;
»-3,714, Ðj»10504’; =
=  =-2, Ðj»116034’.
=-2, Ðj»116034’. ,
, 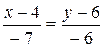 , (x -4)×(-6)=(y -6)×(-7),
, (x -4)×(-6)=(y -6)×(-7), , kAB =
, kAB =  ;
; ,
,  , (x +3)×(-3)= y ×5,
, (x +3)×(-3)= y ×5, , kBC =
, kBC =  ,
,  , (x -4)×(-9)=(y -6)×(-2),
, (x -4)×(-9)=(y -6)×(-2), , kAC =
, kAC =  .
.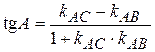 =
=  =
=  =0,75, Ð A»36052’;
=0,75, Ð A»36052’; =
=  =3, Ð B»71034’;
=3, Ð B»71034’; =3, Ð C»71034’.
=3, Ð C»71034’. =
=  , и точка С (2,-3) лежит на (СЕ).
, и точка С (2,-3) лежит на (СЕ). , y +3=
, y +3=  |×6, 6 y +18=-7(x- 2),
|×6, 6 y +18=-7(x- 2), , k 1=
, k 1= 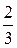 .
.


