
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Складання плоскої системи паралельних силСодержание книги
Поиск на нашем сайте
Система двох паралельних сил, які не утворюють пари, має рівнодійну, паралельну цим силам, причому її модуль дорівнює сумі цих сил, коли сили напрямлені в один бік і різниці модулів, коли вони напрямлені в різні боки. Лінія дії рівнодійної поділяє відстань між точками А, В прикладення сил
У точці С ми малюємо силу, яка буде дорівнювати сумі цих сил.
Лінія дії рівнодіючої
Умови рівноваги плоскої системи довільних сил. Припустимо, що система сил Для рівноваги довільної плоскої системи сил необхідно і досить, щоб алгебраїчні суми:
а) проекцій всіх сил на координатні осі, які лежать в площині дії цих сил, дорівнювали нулю і алгебраїчна сума моментів цих же сил відносно довільної точки даної площини була рівною нулю;
б) моментів усіх сил відносно будь-яких двох точок даної площини дорівнювали нулю і була рівною нулю алгебраїчна сума проекцій цих сил на вісь, не перпендикулярну до прямої, що проходить через дві обрані точки; в) моментів усіх сил відносно трьох довільних точок площини, які не належать одній прямій, дорівнювала нулю.
34. Умови рівноваги плоскої системи довільних сил. Припустимо, що система сил
Для рівноваги довільної плоскої системи сил необхідно і досить, щоб алгебраїчні суми:
г) проекцій всіх сил на координатні осі, які лежать в площині дії цих сил, дорівнювали нулю і алгебраїчна сума моментів цих же сил відносно довільної точки даної площини була рівною нулю;
д) моментів усіх сил відносно будь-яких двох точок даної площини дорівнювали нулю і була рівною нулю алгебраїчна сума проекцій цих сил на вісь, не перпендикулярну до прямої, що проходить через дві обрані точки; 35. Умови рівноваги плоскої системи паралельних сил. Розглянемо в площині Oxy систему сил
Таким чином, для рівноваги плоскої системи паралельних сил необхідно й досить, щоб: а)алгебраїчна сума проекцій сил на координатну вісь, паралельну цим силам, і алгебраїчна сума моментів сил відносно довільної точки площини дорівнювали нулю; б) алгебраїчні суми моментів сил відносно двох певних точок площини, які не лежать на прямій, паралельній лініям дії сил, були рівними нулю. 36. Балочні системи. Різновиди опор та види навантажень. Балкова конструкція розглядає наступні види опор: Закладення - ні переміщень (жорстке закріплення тіла, наприклад, зварювання), виникають реакція невідомої величини і напрямки R і реактивний момент MR. Види навантажень: Зосереджені навантаження передають свою дію через дуже малі площі. Прикладами таких навантажень можуть служити тиск коліс залізничного вагона на рейки, і т. д.
Кінематикою називають розділ теоретичної механіки, в якому вивчаються загальні властивості і якості різних механічних рухів з геометричної точки зору без урахування причин, що викликають і змінюють ці рухи. Кінематику можна розглядати як перехідну ступінь від геометрії до механіки – вона є геометрією чотирьох вимірів, бо крім трьох вимірів, прийнятих в геометрії, запроваджується четвертий – час. Кінематика для свого викладання не потребує ніяких нових аксіом, і спирається на аксіоми евклідової геометрії. В задачах кінематики час приймається за незалежну змінну (аргумент). Відлік часу ведеться від певного початкового моменту, котрий обирають відповідно до конкретних умов задачі. Кінематично задати рух матеріального об’єкту (тіла, точки) – означає задати положення цього об’єкту відносно обраної системи відліку в будь-який момент часу. Якщо положення об’єкта визначається певними параметрами, то необхідно задати залежність параметрів від часу. Така залежність називається кінематичними рівняннями руху або законом руху. Основними питаннями кінематики є виявлення математичних способів задання руху і методів визначення всіх кінематичних величин, що характеризують даний рух. 38Природний спосіб подання точки в кінематиці. Природний спосіб задання руху використовують у випадках, коли траєкторія наперед відома. Тоді положення точки в просторі визначається (рис.2.2) - просторовою кривою - криволінійною (дуговою) координатою - початком відліку дугової координати; - напрямом додатного відліку дугової координати.
Рис. 2.2
При русі точки по траєкторії дугова координата змінюється з часом, тобто Залежність (2.4) називають законом руху точки вздовж заданої траєкторії. Дугову координату не можна плутати з довжиною шляху, який пройшла точка. Шлях точки – це відстань, що пройдена нею за певний проміжок часу, яка вимірюється вздовж траєкторії в напрямку руху точки. Дугова координата – положення точки на траєкторії в даний момент часу. 39Визначення швидкості та прискорення при природному поданні руху точки.
Модуль швидкості визначається за формулою: Якщо Вектор
де Модуль прискорення 40Нормальне та тангенційне прискорення точки. При визначенні прискорення при природному поданні руху точки, ми отримаємо рівняння прискорення: Перший доданок цього рівняння називають тангенціальним (дотичним) прискоренням Так як орти Потрібно чітко уявляти особливості кожної складової повного прискорення. Вектор тангенціального прискорення Кут причому Частинні випадки руху точки. 1. 2. 3. 4. 5. 41. Координатний спосіб подання руху точки. Рівняння руху Положення точки в просторі також можна визначити її декартовими координатами x, y, z залежними від часу Неперервні функції: Рівняння (2.2) одночасно є рівнянням траєкторії точки в параметричній формі, де роль параметра відіграє час Оскільки координати рухомої точки М відповідають координатам кінця вектора 42. Траєкторія, швидкість та прискорення при координатному способі подання руху точки. Щоб визначити траєкторію руху при координатному способі подання руху точки,можна трактувати перші 2 співвідношення як параметричні рівняння кривої: x=x(t); y=y(t). Вилучаючи з цих 2х рівнянь змінну часу,зможемо отримати рівняння плоскої траєкторії точки у явній формі: y=ϕ(x). Знаходження швидкості зводиться до диференціювання рівнянь Модуль швидкості знаходимо за формулою Для визначення прискорення точки потрібно продиференціювати за часом співвідношення рівняння швидкості. Отримаємо: Wz=d2z(t)/dt2. З наведених рівнянь виходить, що проекції прискорення точки на координатні осі дорівнюють першим похідним від проекцій швидкості або другим похідним від відповідних координат точки за часом. Модуль прискорення знаходять за формулою 43Предмет та основні поняття динаміки Динаміка - цеосновний розділ теоретичної механіки, де узагальнюються положення і висновки, отримані в статиці і кінематиці; тобто динаміка вивчає механічний рух матеріальних об’єктів, що виникає під дією сил, прикладених до цих об’єктів. Саме у динаміці ставляться і розв’язуються дві основні задачі механіки: а) за відомим законом руху матеріального об’єкта потрібно визначити сили, які цей рух викликають (перша або пряма задача); б) за відомими силами, що діють на матеріальний об’єкт, потрібно знайти закон його руху (друга або обернена задача). Звичайно динаміку в залежності від конкретного поняття матеріального об’єкта поділяють на три частини: динаміку матеріальної точки, динаміку системи матеріальних точок і динаміку твердого тіла. 44Перша та друга аксіоми динаміки. Перша Аксіома- це Перший закон Ньютона. Згідно цього закону тіло, на яке не діють iншi тiла, або перебуває в спокої, або рухається прямолінійно і рiвномiрно називається вільним, а його рух - вільним рухом або рухом за iнерцiєю. Перший закон Ньютона виконується не у всякій системі відліку (СВ). СВ, в якій виконується перший закон Ньютона, називається iнерцiальною системою вiдлiку (IСВ), а сам закон називають законом iнерцiї. Отже, перший закон Ньютона стверджує, що існує СВ, в якій вільне тіло або знаходиться в спокої, або рухається рiвномiрно i прямолiнiйно. Друга аксіома- Основне рівняння динаміки точки. Сила дорівнює добутку маси на прискорення: P=ma. Оскільки маса-скалярна величина, то вектор сили дорівнює вектору прискорення. Чим більша маса,тим більшу силу треба додати. Отже,маса- міра інертності. А оскільки існує сила тяжіння, то маса є і мірою ваги(тяжіння): G=mg. 45. Третя та четверта аксіоми динаміки. III Аксіома (Закон незалежності дії сил) Якщо на матеріальну точку діє декілька сил водночас, то точка має таке ж прискоерння, яке вона отримає від рівнодіючої цієї системи сил.
Замість того, щоб знайти рівнодіючу прискорень, треба знайти рівнодіючу сил і знайти прискорення як:
Дія сили на точку не залежить від її взіємодії з іншими силами а також від стану руху та спокою точки. IV Аксіома (Закон рівності дії та протидії) Дія двох тіл одне на одне дорівнюють одна одній і спрімовані в протилежні боки.
46. Вільна та невільна точки в динаміці. Матеріальну точку на яку не накладено в'язі - звуть вільною, а її рух - вільним рухом. Також вільна матеріальна точка може займати будь-яке положення, а її рух залежить від початкової швидкості і діючих на неї сил. Невільною, звуть матеріальну точку, на яку накладені деякі в'язі. Відповідно рух такої точки є невільним. Невільна матеріальна точка може набувати будь-яку швидкість та займати будь-яке положення. На основі II i III аксіом, основне рівняння руху матеріальної точки виглядає: При вільному русі, до суми у правій частині рівняння увійдуть тільки активні сили. Для того, щоб дослідити рух невільної точки, в динаміці застосовують принцип звільнення від в'язей, відомий нам зі статики, тобто спочатку розглядають всі в'язі, що впливають на матеріальну точку і замінюють їх дію реакціями, надалі невільну точку можна розглядати як звільнену, щодо якої у суму
|
||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.120.131 (0.008 с.) |

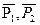 на частини, обернено пропорційні модулям цих сил внутрішнім способом, якщо сили напрямлені в один бік і зовнішнім способом, якщо вони напрямлені в різні боки.
на частини, обернено пропорційні модулям цих сил внутрішнім способом, якщо сили напрямлені в один бік і зовнішнім способом, якщо вони напрямлені в різні боки.



 внутрішнім або зовнішнім чином ділить відстань між точками докладання сил
внутрішнім або зовнішнім чином ділить відстань між точками докладання сил  та
та  на частини обернено пропорційні модулям цих сил, тобто
на частини обернено пропорційні модулям цих сил, тобто
 розташована в площині Oxy.
розташована в площині Oxy. ;
;  ,
,  або
або  ;
; ;
;  ;
;  або
або 
 Тоді умова
Тоді умова 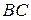 (траєкторією точки);
(траєкторією точки); на траекторії;
на траекторії;
 .(2.4)
.(2.4)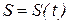 - закон руху точки по траєкторії. Функція
- закон руху точки по траєкторії. Функція  (вектор
(вектор  спрямований за дотичною
спрямований за дотичною  до траєкторії у бік руху точки, а прискорення розкладається на два взаємно-перпендикулярних вектори
до траєкторії у бік руху точки, а прискорення розкладається на два взаємно-перпендикулярних вектори  і
і  , модулі яких дорівнюють
, модулі яких дорівнюють  ,
,  , де ‑
, де ‑ 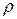 - радіус кривизни траєкторії в точці.
- радіус кривизни траєкторії в точці.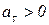 , то вектор
, то вектор  .
. до траєкторії точки у бік угнутості кривої, тобто по
до траєкторії точки у бік угнутості кривої, тобто по  ,
, ‑ орт нормалі.
‑ орт нормалі. .
.  .
. , а другий – нормальним або доцентровим прискоренням
, а другий – нормальним або доцентровим прискоренням  :
:  .
.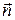 і
і  лежать в стичній площині, то і вектор
лежать в стичній площині, то і вектор 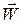 також буде лежати в цій площині. Таким чином, повне прискорення точки в загальному випадку криволінійного руху:
також буде лежати в цій площині. Таким чином, повне прискорення точки в загальному випадку криволінійного руху:  .
. напрямлений по дотичній до траєкторії точки і характеризує зміну модуля швидкості точки. Величина
напрямлений по дотичній до траєкторії точки і характеризує зміну модуля швидкості точки. Величина  завжди напрямлений в бік угнутості траєкторії і характеризує зміну вектора швидкості точки за напрямом. Величина
завжди напрямлений в бік угнутості траєкторії і характеризує зміну вектора швидкості точки за напрямом. Величина  відхилення вектора
відхилення вектора  знаходять зі співвідношення:
знаходять зі співвідношення: 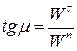
 .
.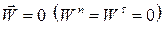 – прямолінійний рівномірний рух.
– прямолінійний рівномірний рух. – прямолінійний рівнозмінний рух.
– прямолінійний рівнозмінний рух. – рівномірний рух точки вздовж криволінійної траєкторії будь-якої форми, або момент екстремального значення швидкості.
– рівномірний рух точки вздовж криволінійної траєкторії будь-якої форми, або момент екстремального значення швидкості. – рівнозмінний криволінійний рух.
– рівнозмінний криволінійний рух. – прямолінійний рух точки; момент часу, коли рухома точка знаходиться в точці перегину траєкторії, або моменти часу зміни напряму руху точки вздовж траєкторії.
– прямолінійний рух точки; момент часу, коли рухома точка знаходиться в точці перегину траєкторії, або моменти часу зміни напряму руху точки вздовж траєкторії. .
. (2.2) які називають кінематичними рівняннями, визначають закон руху точки в прямокутних декартових координатах.
(2.2) які називають кінематичними рівняннями, визначають закон руху точки в прямокутних декартових координатах. в системі
в системі  , то між векторним і координатним способами задання руху існує зв’язок у формі рівняння:
, то між векторним і координатним способами задання руху існує зв’язок у формі рівняння:  .
. ; Vx=dx(t)/dt; Vy=dy(t)/dt; Vz=dz(t)/dt.
; Vx=dx(t)/dt; Vy=dy(t)/dt; Vz=dz(t)/dt. , а її напрям визначається напрямляючими косинусами:
, а її напрям визначається напрямляючими косинусами:  .
.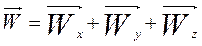 ; Wx=d2x(t)/dt2; Wy=d2y(t)/dt2;
; Wx=d2x(t)/dt2; Wy=d2y(t)/dt2; , а напрям визначають напрямляючі косинуси:
, а напрям визначають напрямляючі косинуси: 




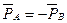
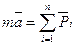
 увійдуть як активні сили, так і відкинуті реакції в'язей.
увійдуть як активні сили, так і відкинуті реакції в'язей.


