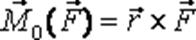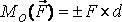Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стрижневі системи з ідеальними шарнірамиСодержание книги
Похожие статьи вашей тематики
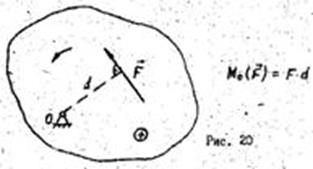
Поиск на нашем сайте Шарнір, в якому відсутнє тертя, називають идеальним.Геометріческі незмінна конструкция гратчастого типу, що складається з прямолінійних невагомих стрижнів, з'єднаних ідеальними шарнірами, називається фермою (що показано на малюнку). Шарніри ферми називаються узламі.Все активні сили у фермі включені тільки до вузлів Використання ферм в техніці дозволяє значно облегшіть вага конструкцій. Така ферма з ідеальними шарнірами і невагомими стержнями-ідеалізована розрахункова схема, в якій всі стрижні відчувають тільки розтягують або стискають зусилля. Насправді ж стрижні мають вагу, з'єднані жорсткими косинками за допомогою зварювання і працюють на вигин. Однак якщо зовнішні навантаження значно перевищують ваги стрижнем і прикладені у вузлах, то прийнята розрахункова схема досить добре описує реальне навантаження стрижнем. Верхні і нижні стрижні, створюючі зовнішній контур ферми, називаються відповідно верхнім і нижнім поясамі.Решетка ферми утворюється з вертикальних стійок і похилих розкосів.
Момент пари сил. Властивості пар Парою сил називається система двох рівних по модулю, паралельних і направлених в протилежні сторони сил, що діють на абсолютно тверде тіло. Моментом пари зветься величина, що дорівнює взятому з відповідним знаком добутку модуля однієї з сил пари на її плече (Поняття моменту сили пов'язане з точкою, відносно якої береться момент. Момент пари визначається тільки її моментом і плечем; ні з якою точкою площині ця величина не пов'язана). Властивості: сума моментів сил пари щодо точки не залежить від вибору точки і завжди дорівнює моменту пари, Пара сил не має рівнодіюча - не можна врівноважити однією силою. Додавання пар сил. Система пар, що лежать в одній площині, еквівалентна одній парі, що лежить втій же площині і має момент, рівний алгебраїчної сумі моментів доданків пар.
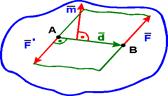
Теорія пар сил на площині Система двох рівних по модулю, паралельних і направлених в протилежні сторони сил називається парою сил (F = - Fў). Площина, в якій лежать сили F і Fў, називається площиною пари, а найкоротша відстань d між лініями дії сил - плечем пари.Пара сил не має рівнодіючої, так як R = F + Fў = 0. Дія пари сил F, Fў на абсолютно тверде тіло зводиться до обертального ефекту, який характеризується моментом пари. Моментом пари називається вектор m = dґF, модуль якого дорівнює добутку модуля однієї з сил пари на її плече. | M | = | F | Ч | d |. Вектор m спрямований на площині пари в ту сторону, звідки пара видно прагне повернути тіло проти годинникової стрілки. Момент пари m - вектор вільний, тобто його можна прикладати у будь-якій точці тіла.
Теорема 1. Пари сил з рівними моментами еквівалентні. наслідки: 1. Пару сил, прикладену до твердого тіла, можна замінити іншою парою в тій же площині, якщо при такій заміні не змінюється величина моменту пари і його напрям: m1 = d1ґF1 = m2 = d2ґF2 або d1ґF1 = d2ґF2. 2. Пару сил можна переносити в площину, паралельну площині пари. Теорема 2. Сукупність декількох пар з моментами m1, m2,..., mn еквівалентна одній парі, момент m якої дорівнює геометричній сумі моментів даних пар: m = m1 + m2 +... + Mn. Для пар, що лежать в одній площині, користуються поняттям алгебраїчного моменту пари. Алгебраїчний момент пари дорівнює взятому з відповідним знаком добутку модуля однієї з сил пари на плече пари: m = ± FЧd.
25.Еквівалентність пар сил. Складання пар сил.
Припустимо, на тіло діють три пари (рис. а), моменти яких Як відомо, рівнодіюча сил, що діють уздовж однієї прямої, спрямована по тій же прямій і модуль її дорівнює алгебраїчній сумі складових сил. Тому, склавши сили, прикладені до точок Момент рівнодійної пари, а так як або Поширюючи рівність Отже, для того щоб скласти будь-яке число пар, що діють на тіло в одній площині, досить алгебраїчно скласти моменти цих пар. Отриманий в результаті складання момент і визначає рівнодіючу пару сил. Якщо в результаті складання пар Значить, систему пар або одну пару можна врівноважити тільки парою.
Умови рівноваги пар сил Плоска система пар, що лежить в одній площині або в паралельних площинах, еквівалентна одній рівнодіючій парі, момент якої дорівнює алгебраїчній сумі моментів пар, що складаються:
Враховуючи, що систему діючих на тіло пар сил завжди можна замінити однією еквівалентною парою сил, для рівноваги системи пар необхідно і достатньо, щоб момент результуючої пари сил дорівнював нулю. Тоді, відповідно до формули одержимо умову рівноваги системи пар:
Проеціюючи векторне рівняння на координатні осі, одержимо три алгебраїчних рівняння умов рівноваги системи пари сил:
Для системи пар сил, що лежать в одній площині, необхідно і достатньо, щоб алгебраїчна сума моментів цих пар дорівнювала нулю.
Момент сили відносно точки Векторним моментом сили відносно точки називається векторний добуток радіуса-вектора проведеного із точки відносно якої обчислюється момент на вектор сили, тобто (рис. 20)
. Плечем сили відносно точки називається довжина перпендикуляра, опущеного із точки відносно якої обчислюється момент на лінію дії сили.
Або іншими словами можна сказати: векторним моментом сили відносно точки називається вектор модуль якого дорівнює добутку модуля сили на плече. Цей вектор перпендикулярний до площини у якій лежать вектор сили і точка відносно якої обчислюється момент і напрямлений у такий бік, якщо дивитися з його кінця, то видно намагання сили повернути тіло проти ходу стрілки годинника. Властивості векторного момента сили відносно точки 1) векторний момент сили відносно точки не змінюється при переносі точки прикладання сили уздовж її лінії дії; 2) векторний момент сили відносно точки дорівнює нулеві, якщо лінія дії сили проходить через точку, відносно якої обчислюється момент (плече дорівнює нулеві). Якщо розглядається плоска система сил то вводиться поняття алгебраїчного момента сили відносно точки.
Алгебраїчним моментом сили відносно точки називається взятий з відповідним знаком добуток модуля сили на плече. Знак плюс береться у тому випадку якщо сила намагається повернути тіло відносно даної точки проти ходу стрілки годинника.
|
||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 464; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

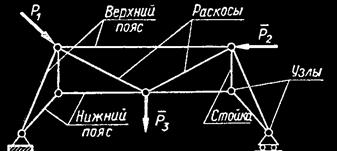
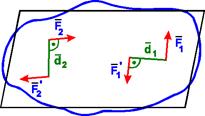 Знак плюс відповідає повороту тіла під дією пари проти годинникової стрілки, мінус - по ходу годинникової стрілки: m1 = F1Чd1, m2 = - F2Чd2.
Знак плюс відповідає повороту тіла під дією пари проти годинникової стрілки, мінус - по ходу годинникової стрілки: m1 = F1Чd1, m2 = - F2Чd2.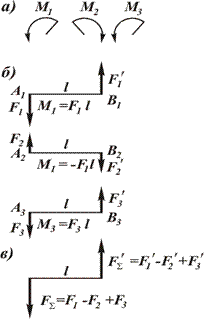 Теорема. Система пар, що діють на тіло в одній площині, еквівалентна парі сил з моментом, рівним алгебраїчній сумі моментів пар системи.
Теорема. Система пар, що діють на тіло в одній площині, еквівалентна парі сил з моментом, рівним алгебраїчній сумі моментів пар системи. ,,.
,,. 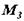 ,
, 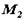 відомі. Кожну із заданих пар замінимо еквівалентної парою відповідно
відомі. Кожну із заданих пар замінимо еквівалентної парою відповідно  ,
,  ,
, 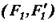 , але з однаковими плечима
, але з однаковими плечима  , т. e.
, т. e. 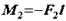 ,
, 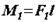 ,
,  Та розташуємо ці пари так, щоб їх сили діяли уздовж двох паралельних прямих (мал. б).
Та розташуємо ці пари так, щоб їх сили діяли уздовж двох паралельних прямих (мал. б).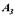

 і до точок
і до точок 
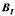
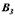 отримаємо рівнодіючу пару
отримаємо рівнодіючу пару 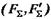 , еквівалентну трьом заданим парам (рис. в). При цьому.
, еквівалентну трьом заданим парам (рис. в). При цьому. 
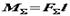
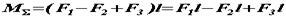
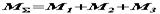 . Теорема доведена.
. Теорема доведена.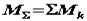
 , то діючі на тіло пари утворюють врівноважену систему. Отже, необхідна і достатня умова рівноваги системи пар виражається одним рівнянням
, то діючі на тіло пари утворюють врівноважену систему. Отже, необхідна і достатня умова рівноваги системи пар виражається одним рівнянням 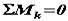 ,тобто для рівноваги системи пар сил, що діють на тіло в одній площині, необхідно і достатньо, щоб алгебраїчна сума їх моментів дорівнювала нулю.
,тобто для рівноваги системи пар сил, що діють на тіло в одній площині, необхідно і достатньо, щоб алгебраїчна сума їх моментів дорівнювала нулю.
 .
. ;
;  ;
; 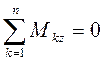 .
.