
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет і задачі статики. Приклади.Содержание книги
Поиск на нашем сайте Статика - розділ теоретичної механіки, в якому розглядають властивості сил, прикладених до точок твердого тіла, і умови їхньої рівноваги. Основні завдання: А зараз розглянемо її основні поняття: Сила – це кількісна міра механічної взаємодії двох тіл, яка визначає характер, величину та напрямок взаємодії. З цього класичного визначення сили випливає, що вона є величиною векторною, а тому є три визначальних параметри: величина сили (або модуль), напрямок дії та точка прикладання. На розрахунково – силових схемах силу зображують у вигляді вектора довільної довжини (крім випадків графічної статики, коли силу креслять у масштабі). Покажемо, наприклад, (рис. 1.1) довільну силу
Рис. 1.1
Одиницею вимірювання сили є 1 Ньютон – [ На тіло можуть одночасно діяти декілька сил, утворюючи систему. Система сил – це сукупність декількох сил, які діють на тіло.Введемо ще деякі поняття, що пов'язані з силою. Аксіоми статики та приклади їх застосування. В основі статики лежать аксіоми, що встановлюють основні властивості сил, докладених до мат.точки та абсолютно твердого тіла. Аксіоми: Аксіома 1. Дві сили, прикладені до вільного абсолютно твердого тіла, взаємно врівноважуються тоді і тільки тоді, коли вони рівні за модулем (F1 = F2) і спрямовані вздовж загальної лінії дії в протилежні сторони
Аксіома 2. Дві сили, що діють на тверде тіло, взаємно зрівноважуються тоді й тільки тоді, коли вони рівні за величиною, протилежні за напрямком і діють уздовж однієї прямої. Аксіома 3 (аксіома приєднання або вилучення взаємно зрівноважених сил). Дія системи сил на тверде тіло не зміниться, якщо до неї приєднати або з неї вилучити систему взаємно зрівноважених сил.
Наслідок. Не змінюючи дії сили на тверде тіло, її можна переносити уздовж лінії дії сили, зберігаючи незмінним її величину та напрямок. Аксіома 4 (аксіома паралелограма сил). Рівнодійна двох сил, лінії дії яких перетинаються, прикладена у точці їх перетину і визначається діагоналлю паралелограма, побудованого на цих силах.
Процес визначення рівнодійної називають додаванням сил. Аксіома 5 (третій закон Ньютона). Усякій дії відповідає рівна і протилежно напрямлена протидія. При взаємодії двох матеріальних точок виникають сили взаємодії. Одну з них умовно називають дія, а другу – протидія. Аксіома 6 (принцип твердіння). Рівновага деформованого тіла під дією прикладених сил зберігається при його затвердінні. Під твердінням розуміють уявне перетворення реального тіла на абсолютно тверде. При цьому припускають, що сили, які прикладені до тіла, зберігають свої величини, напрямки дій і точки прикладання. Сенс аксіоми полягає в тому, що при вивченні рівноваги реальних тіл можна користуватися рівняннями рівноваги, які отримані для абсолютно твердих тіл.
Наслідки з аксіом статики. Наслідок з перших двох аксіом. Точку прикладання сили можна пересувати в межах даного тіла вздовж лінії дії сили (сила є ковзним вектором).
Рис. 1.3
Припустимо, що на тіло (рис. 1.3) діє вектор сили Але цю систему трьох сил можна розглядати по іншому: як силу Наслідок з 3 аксіоми:
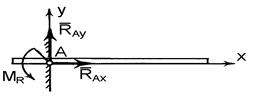
12.Основні вязі та реакції. Креслення,реакції. Розглянемо основні типи в'язей як розрахункові моделі. Кожна з цих в'язей має свою назву, графічне зображення і свої реакції. 1. Ідеально гладенька площина або опора (рис. 1.5, а). Реакція цієї в'язі а б в г
д е
ж з и
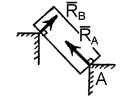
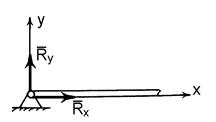
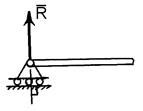
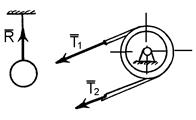
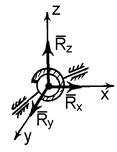
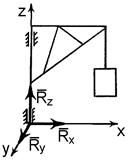
2. Точкова опора (рис. 1.5, б). Якщо гладенька площина вироджується у лінію або точку, то реакція в'язей 3. Шарнірно – нерухома опора або нерухомий шарнір (рис. 1.5, в). Реакція шарнірно – нерухомої опори прикладена у центрі шарніра і невідома за напрямком. 4. Шарнірно – рухома опора або каток (рис. 1.5, г). Реакція цієї в'язі 5. Жорстке закріплення (рис. 1.5, д). Реакція цієї в'язі повинна бути представлена двома складовими у вигляді сил 6. Ідеальний стержень, тобто невагомий тонкий стержень, на кінцях якого встановлені циліндричні шарніри і який працює тільки на розтяг або на стиск (рис. 1.5, е). 7. Гнучка нитка або в'язь, яка здійснюється ідеальними гнучкими тілами, тобто невагомими, нерозтяжними нитками: канатами, пасами, ланцюгами (рис. 5.1, ж). 8. Сферичний шарнір або його частковий випадок – підп'ятник (рис. 1.5, з, и). Реакція цієї в'язі повинна бути зображеною трьома складовими у вигляді реакцій
|
||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 594; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 , яка зображена у вигляді вектора
, яка зображена у вигляді вектора  , прикладена у точці
, прикладена у точці  і діє вздовж лінії
і діє вздовж лінії  .
.
 ] або 1 кілоньютон [
] або 1 кілоньютон [  ]. 1
]. 1  . У технічній системі одиницею вимірювання сили є 1 кілограм сили – [
. У технічній системі одиницею вимірювання сили є 1 кілограм сили – [  ] або [ кгс ].
] або [ кгс ].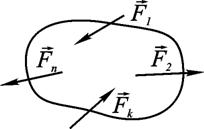 Еквівалентні системи сил – це такі системи сил, які на одне і теж тіло діють однаково. Система сил може бути, в деяких випадках, еквівалентна нулю. Рівнодійна сила системи сил – це така сила, дія якої еквівалентна дії всієї системи сил. Зрівноважуюча сила – це сила, яка за величиною дорівнює рівнодійній силі, лежить з нею на одній прямій, але протилежна за напрямом.
Еквівалентні системи сил – це такі системи сил, які на одне і теж тіло діють однаково. Система сил може бути, в деяких випадках, еквівалентна нулю. Рівнодійна сила системи сил – це така сила, дія якої еквівалентна дії всієї системи сил. Зрівноважуюча сила – це сила, яка за величиною дорівнює рівнодійній силі, лежить з нею на одній прямій, але протилежна за напрямом.



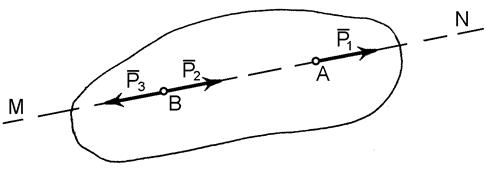
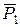 , який прикладений в точці
, який прикладений в точці  на лінії дії
на лінії дії 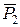 і
і 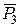 , такі, що
, такі, що 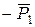 . Згідно першої аксіоми ці сили зрівноважені, а згідно другої аксіоми їх можна приєднати, не змінюючи кінематичного стану тіла.
. Згідно першої аксіоми ці сили зрівноважені, а згідно другої аксіоми їх можна приєднати, не змінюючи кінематичного стану тіла.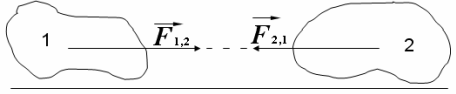
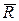 напрямлена перпендикулярно до площини, або розташована вздовж нормалі.
напрямлена перпендикулярно до площини, або розташована вздовж нормалі. 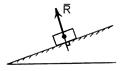

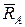 і
і 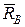 буде спрямована по перпендикуляру до лінії (поверхні) тіла, яке утримується в даній точці.
буде спрямована по перпендикуляру до лінії (поверхні) тіла, яке утримується в даній точці.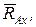 і
і 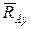 та реактивного моменту
та реактивного моменту 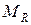 .
.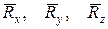 , напрямлених вздовж осей просторової декартової системи координат
, напрямлених вздовж осей просторової декартової системи координат 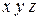 , з початком у центрі сферичного шарніра або підп'ятника.
, з початком у центрі сферичного шарніра або підп'ятника.


