
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Місце теоретичної механіки в системі технічних наук.Содержание книги
Поиск на нашем сайте Місце теоретичної механіки в системі технічних наук. У технічних науках під теоретичною механікою мається на увазі набір фізико-математичних методів, що полегшують розрахунки механізмів, споруд, літальних апаратів і т. п. (так звана прикладна механіка або інженерна механіка). Практично завжди ці методи виводяться із законів класичної механіки - в основному, із законів Ньютона, хоча в деяких технічних завданнях виявляються корисними деякі з методів аналітичної механіки. В основі теоретичної механіки лежать закони Ньютона, тому вона називається ньютонівською або класичною. Класична механіка з великою точністю задовольняє багатьом галузям сучасної техніки при швидкостях руху тіл, досить малих у порівнянні зі швидкістю світла. Теоретична механіка спирається на деяку кількість законів, встановлених у дослідній механіці, прийнятих за істини, що не вимагають доказів - аксіоми. Спираючись на аксіоми як на відомий і перевірений практикою і експериментом фундамент, теоретична механіка зводить свою будівлю за допомогою строгих математичних висновків. Абстрагуючись при вивченні руху матеріальних тіл від усього часткового, теоретична механіка Теоретична механіка як частина природознавства, що використовує математичні методи, розглядає тільки ті властивості, які в даній задачі є визначальними. Це приводить до розгляду різних моделей матеріальних тіл:
Матеріальною точкою називається тіло, розмірами якого можна знехтувати при розв'язанні певних задач. Наприклад, при наближеному дослідженні рухів планет їх можна розглядати як матеріальні точки. Абсолютно твердим називається тіло, відстань між будь-якими точками якого не змінюється під час рівноваги або руху. Теоретична механіка стала основою для створення багатьох прикладних напрямів, які отримали великий розвиток. Це механіка рідини і газу, механіка деформівного твердого тіла, теорія коливань, динаміка та міцність машин, гіроскопії, теорія управління, теорія польоту, навігація та багато інших. Слід розуміти, що матеріальна точка, абсолютно тверде тіло і механічна система є поняттями абстрактними і лише наближено відображають реальний світ. Але використання цих абстракцій значно спрощує дослідження рівноваги та руху дійсних матеріальних об'єктів. Рівнодіюча система сил.Приклади. Якщо на дане тіло діє одночасно декілька сил, то їх дію на рух тіла можна замінити дією однієї сіли. Таку заміну називають складанням сил. Дані сили називають складовими, а замінюючу їх силу - рівнодіючою(або їх сумою). Рівнодіюча сил - це сила, яка замінює дію кількох сил. Рівнодіюча сила дорівнює геометричній сумі всіх сил системи. Рівнодіюча сила - теж сила і підкоряється всім їхніми правилами.. Система сил має рівнодіючу тільки в тому випадку, якщо для неї існує точка, відносно якої,головний момент сил системи, дорівнює нулю.
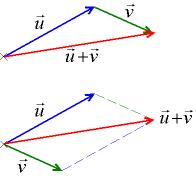
1) Правило трикутника. Для складання двох векторів U та V (поставити зверху вектори) за правилом трикутника обидва ці вектора переносяться паралельно самим собі так, щоб початок одного з них збігався з кінцем іншого. Тоді вектор суми задається третьою стороною трикутника, причому його початок збігається з початком першого вектора, а кінець з кінцем другого вектора. (мал.1) 2) Правило паралелограма. Для складання двох векторів U та V (поставити зверху вектори) за правилом паралелограма обидва ці вектора переносяться паралельно самим собі так, щоб їх початку збігалися. Тоді вектор суми задається діагоналлю побудованого на них паралелограма, яка з їх загального початку. (мал.1)
Рівнодіюча системи сил, наприклад двох сил, рівних за величиною і протилежних за напрямком, дорівнює нулю.
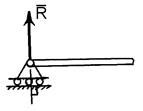
Наслідки з аксіом статики. Наслідок з перших двох аксіом. Точку прикладання сили можна пересувати в межах даного тіла вздовж лінії дії сили (сила є ковзним вектором).
Рис. 1.3
Припустимо, що на тіло (рис. 1.3) діє вектор сили Але цю систему трьох сил можна розглядати по іншому: як силу Наслідок з 3 аксіоми:
12.Основні вязі та реакції. Креслення,реакції. Розглянемо основні типи в'язей як розрахункові моделі. Кожна з цих в'язей має свою назву, графічне зображення і свої реакції. 1. Ідеально гладенька площина або опора (рис. 1.5, а). Реакція цієї в'язі а б в г
д е
ж з и
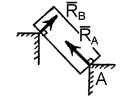
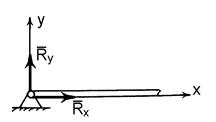
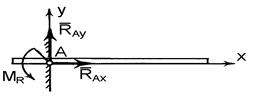
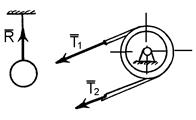
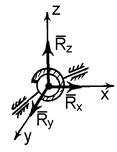
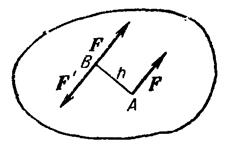
2. Точкова опора (рис. 1.5, б). Якщо гладенька площина вироджується у лінію або точку, то реакція в'язей 3. Шарнірно – нерухома опора або нерухомий шарнір (рис. 1.5, в). Реакція шарнірно – нерухомої опори прикладена у центрі шарніра і невідома за напрямком. 4. Шарнірно – рухома опора або каток (рис. 1.5, г). Реакція цієї в'язі 5. Жорстке закріплення (рис. 1.5, д). Реакція цієї в'язі повинна бути представлена двома складовими у вигляді сил 6. Ідеальний стержень, тобто невагомий тонкий стержень, на кінцях якого встановлені циліндричні шарніри і який працює тільки на розтяг або на стиск (рис. 1.5, е). 7. Гнучка нитка або в'язь, яка здійснюється ідеальними гнучкими тілами, тобто невагомими, нерозтяжними нитками: канатами, пасами, ланцюгами (рис. 5.1, ж). 8. Сферичний шарнір або його частковий випадок – підп'ятник (рис. 1.5, з, и). Реакція цієї в'язі повинна бути зображеною трьома складовими у вигляді реакцій Теорія пар сил на площині Система двох рівних по модулю, паралельних і направлених в протилежні сторони сил називається парою сил (F = - Fў). Площина, в якій лежать сили F і Fў, називається площиною пари, а найкоротша відстань d між лініями дії сил - плечем пари.Пара сил не має рівнодіючої, так як R = F + Fў = 0. Дія пари сил F, Fў на абсолютно тверде тіло зводиться до обертального ефекту, який характеризується моментом пари. Моментом пари називається вектор m = dґF, модуль якого дорівнює добутку модуля однієї з сил пари на її плече. | M | = | F | Ч | d |. Вектор m спрямований на площині пари в ту сторону, звідки пара видно прагне повернути тіло проти годинникової стрілки. Момент пари m - вектор вільний, тобто його можна прикладати у будь-якій точці тіла.
Теорема 1. Пари сил з рівними моментами еквівалентні. наслідки: 1. Пару сил, прикладену до твердого тіла, можна замінити іншою парою в тій же площині, якщо при такій заміні не змінюється величина моменту пари і його напрям: m1 = d1ґF1 = m2 = d2ґF2 або d1ґF1 = d2ґF2. 2. Пару сил можна переносити в площину, паралельну площині пари. Теорема 2. Сукупність декількох пар з моментами m1, m2,..., mn еквівалентна одній парі, момент m якої дорівнює геометричній сумі моментів даних пар: m = m1 + m2 +... + Mn. Для пар, що лежать в одній площині, користуються поняттям алгебраїчного моменту пари. Алгебраїчний момент пари дорівнює взятому з відповідним знаком добутку модуля однієї з сил пари на плече пари: m = ± FЧd.
25.Еквівалентність пар сил. Складання пар сил.
Припустимо, на тіло діють три пари (рис. а), моменти яких Як відомо, рівнодіюча сил, що діють уздовж однієї прямої, спрямована по тій же прямій і модуль її дорівнює алгебраїчній сумі складових сил. Тому, склавши сили, прикладені до точок Момент рівнодійної пари, а так як або Поширюючи рівність Отже, для того щоб скласти будь-яке число пар, що діють на тіло в одній площині, досить алгебраїчно скласти моменти цих пар. Отриманий в результаті складання момент і визначає рівнодіючу пару сил. Якщо в результаті складання пар Значить, систему пар або одну пару можна врівноважити тільки парою.
Умови рівноваги пар сил Плоска система пар, що лежить в одній площині або в паралельних площинах, еквівалентна одній рівнодіючій парі, момент якої дорівнює алгебраїчній сумі моментів пар, що складаються:
Враховуючи, що систему діючих на тіло пар сил завжди можна замінити однією еквівалентною парою сил, для рівноваги системи пар необхідно і достатньо, щоб момент результуючої пари сил дорівнював нулю. Тоді, відповідно до формули одержимо умову рівноваги системи пар:
Проеціюючи векторне рівняння на координатні осі, одержимо три алгебраїчних рівняння умов рівноваги системи пари сил:
Для системи пар сил, що лежать в одній площині, необхідно і достатньо, щоб алгебраїчна сума моментів цих пар дорівнювала нулю.
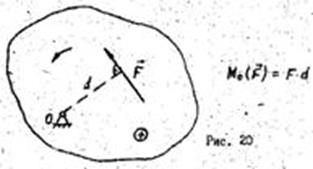
Момент сили відносно точки Векторним моментом сили відносно точки називається векторний добуток радіуса-вектора проведеного із точки відносно якої обчислюється момент на вектор сили, тобто (рис. 20)
. Плечем сили відносно точки називається довжина перпендикуляра, опущеного із точки відносно якої обчислюється момент на лінію дії сили.
Або іншими словами можна сказати: векторним моментом сили відносно точки називається вектор модуль якого дорівнює добутку модуля сили на плече. Цей вектор перпендикулярний до площини у якій лежать вектор сили і точка відносно якої обчислюється момент і напрямлений у такий бік, якщо дивитися з його кінця, то видно намагання сили повернути тіло проти ходу стрілки годинника. Властивості векторного момента сили відносно точки 1) векторний момент сили відносно точки не змінюється при переносі точки прикладання сили уздовж її лінії дії; 2) векторний момент сили відносно точки дорівнює нулеві, якщо лінія дії сили проходить через точку, відносно якої обчислюється момент (плече дорівнює нулеві). Якщо розглядається плоска система сил то вводиться поняття алгебраїчного момента сили відносно точки.
Алгебраїчним моментом сили відносно точки називається взятий з відповідним знаком добуток модуля сили на плече. Знак плюс береться у тому випадку якщо сила намагається повернути тіло відносно даної точки проти ходу стрілки годинника.
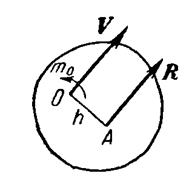
Приведення сили до точки При зведенні сили до даної точки додається приєднана пара сил, момент якої дорівнює моменту даної сили відносно центра зведення. Це означає, що не порушуючи стану твердого тіла, можна силу F прикласти до точки В, додавши приєднану пару сил, момент якої дорівнює моменту заданої сили F відносно центра зведення В.
Головним вектором V зветься векторна сума сил, прикладених до твердого тіла, тобто
Проекції головного вектора Vx та Vv на вісі декартових координат дорівнюють сумам проекцій даних сил на відповідні вісі:
Модуль головного вектора:
Напрямляючі косинуси головного вектора визначаються за формулами:
Головним моментом точки відносно центра О зветься сума моментів сил, прикладених до твердого тіла, відносно цього центра, тобто
Теорема Варіньйона Момент рівнодіючої плоскої системи сил відносно довільного центра, що лежить в площині дії цих сил, дорівнює алгебраїчній сумі моментів сил даної системи відносно того ж центра.
Місце теоретичної механіки в системі технічних наук. У технічних науках під теоретичною механікою мається на увазі набір фізико-математичних методів, що полегшують розрахунки механізмів, споруд, літальних апаратів і т. п. (так звана прикладна механіка або інженерна механіка). Практично завжди ці методи виводяться із законів класичної механіки - в основному, із законів Ньютона, хоча в деяких технічних завданнях виявляються корисними деякі з методів аналітичної механіки. В основі теоретичної механіки лежать закони Ньютона, тому вона називається ньютонівською або класичною. Класична механіка з великою точністю задовольняє багатьом галузям сучасної техніки при швидкостях руху тіл, досить малих у порівнянні зі швидкістю світла. Теоретична механіка спирається на деяку кількість законів, встановлених у дослідній механіці, прийнятих за істини, що не вимагають доказів - аксіоми. Спираючись на аксіоми як на відомий і перевірений практикою і експериментом фундамент, теоретична механіка зводить свою будівлю за допомогою строгих математичних висновків. Абстрагуючись при вивченні руху матеріальних тіл від усього часткового, теоретична механіка Теоретична механіка як частина природознавства, що використовує математичні методи, розглядає тільки ті властивості, які в даній задачі є визначальними. Це приводить до розгляду різних моделей матеріальних тіл:
Матеріальною точкою називається тіло, розмірами якого можна знехтувати при розв'язанні певних задач. Наприклад, при наближеному дослідженні рухів планет їх можна розглядати як матеріальні точки. Абсолютно твердим називається тіло, відстань між будь-якими точками якого не змінюється під час рівноваги або руху. Теоретична механіка стала основою для створення багатьох прикладних напрямів, які отримали великий розвиток. Це механіка рідини і газу, механіка деформівного твердого тіла, теорія коливань, динаміка та міцність машин, гіроскопії, теорія управління, теорія польоту, навігація та багато інших. Слід розуміти, що матеріальна точка, абсолютно тверде тіло і механічна система є поняттями абстрактними і лише наближено відображають реальний світ. Але використання цих абстракцій значно спрощує дослідження рівноваги та руху дійсних матеріальних об'єктів.
|
||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (мал.1)
(мал.1)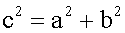
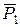 , який прикладений в точці
, який прикладений в точці  і має лінію дії
і має лінію дії  . Прикладемо в довільній точці
. Прикладемо в довільній точці  на лінії дії
на лінії дії 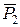 і
і 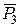 , такі, що
, такі, що 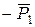 . Згідно першої аксіоми ці сили зрівноважені, а згідно другої аксіоми їх можна приєднати, не змінюючи кінематичного стану тіла.
. Згідно першої аксіоми ці сили зрівноважені, а згідно другої аксіоми їх можна приєднати, не змінюючи кінематичного стану тіла.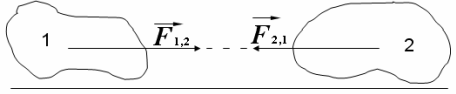
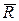 напрямлена перпендикулярно до площини, або розташована вздовж нормалі.
напрямлена перпендикулярно до площини, або розташована вздовж нормалі. 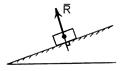

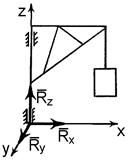
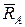 і
і 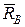 буде спрямована по перпендикуляру до лінії (поверхні) тіла, яке утримується в даній точці.
буде спрямована по перпендикуляру до лінії (поверхні) тіла, яке утримується в даній точці.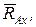 і
і 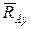 та реактивного моменту
та реактивного моменту 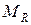 .
.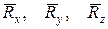 , напрямлених вздовж осей просторової декартової системи координат
, напрямлених вздовж осей просторової декартової системи координат 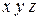 , з початком у центрі сферичного шарніра або підп'ятника.
, з початком у центрі сферичного шарніра або підп'ятника.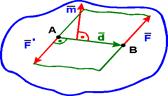
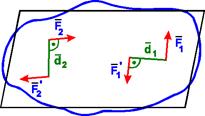 Знак плюс відповідає повороту тіла під дією пари проти годинникової стрілки, мінус - по ходу годинникової стрілки: m1 = F1Чd1, m2 = - F2Чd2.
Знак плюс відповідає повороту тіла під дією пари проти годинникової стрілки, мінус - по ходу годинникової стрілки: m1 = F1Чd1, m2 = - F2Чd2.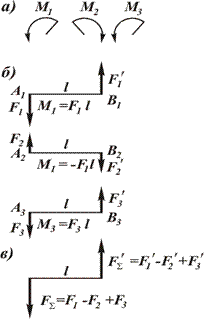 Теорема. Система пар, що діють на тіло в одній площині, еквівалентна парі сил з моментом, рівним алгебраїчній сумі моментів пар системи.
Теорема. Система пар, що діють на тіло в одній площині, еквівалентна парі сил з моментом, рівним алгебраїчній сумі моментів пар системи. ,,.
,,. 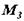 ,
, 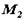 відомі. Кожну із заданих пар замінимо еквівалентної парою відповідно
відомі. Кожну із заданих пар замінимо еквівалентної парою відповідно  ,
,  ,
, 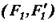 , але з однаковими плечима
, але з однаковими плечима  , т. e.
, т. e. 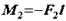 ,
, 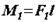 ,
,  Та розташуємо ці пари так, щоб їх сили діяли уздовж двох паралельних прямих (мал. б).
Та розташуємо ці пари так, щоб їх сили діяли уздовж двох паралельних прямих (мал. б).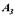

 і до точок
і до точок 
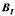
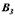 отримаємо рівнодіючу пару
отримаємо рівнодіючу пару 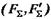 , еквівалентну трьом заданим парам (рис. в). При цьому.
, еквівалентну трьом заданим парам (рис. в). При цьому. 
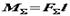
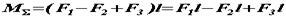
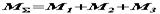 . Теорема доведена.
. Теорема доведена.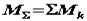
 , то діючі на тіло пари утворюють врівноважену систему. Отже, необхідна і достатня умова рівноваги системи пар виражається одним рівнянням
, то діючі на тіло пари утворюють врівноважену систему. Отже, необхідна і достатня умова рівноваги системи пар виражається одним рівнянням 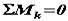 ,тобто для рівноваги системи пар сил, що діють на тіло в одній площині, необхідно і достатньо, щоб алгебраїчна сума їх моментів дорівнювала нулю.
,тобто для рівноваги системи пар сил, що діють на тіло в одній площині, необхідно і достатньо, щоб алгебраїчна сума їх моментів дорівнювала нулю.
 .
. ;
;  ;
; 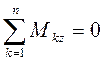 .
.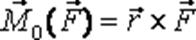

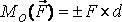
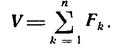
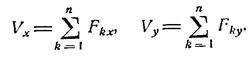
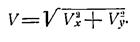
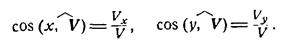

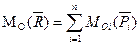 .
.


