
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порівняння математичних виразівСодержание книги Поиск на нашем сайте
В 2-му класі продовжується робота над порівнянням чисел, числа та виразу, двох математичних виразів. Порівняти математичні вирази – це означає встановити, значення якого виразу більше, менше або вони рівні. Вирази порівнюються декількома способами: 1. Знаходимо значення кожного виразу і порівнюємо отримані числа. Більше той вираз, значення якого більше. І навпаки. 2. Порівнюємо вирази, аналізуючи їх: 3×5 …3×4 - обидва вирази – добутки; в обох добутках однакові перші множники, значить більший той вираз у якого другий множник більший: 5 більш ніж 4,тому 3×5 більше 3×4. 3. Перетворення виразу й порівняння виразів 2-им способом: Розглянемо ці способи докладно. Спочатку учні вчаться порівнювати вираз і число, наприклад: 8 + 5 і 12. Першим кроком знаходимо значення суми: 8 + 5 = 13. Другим кроком порівнюємо отриманий результат з числом 12: 13 > 12. Третім кроком робимо висновок: якщо 13 > 12, то 8 + 5 > 12. Форма запису в зошиті:
Далі порівнюються два математичні вирази. Треба порівняти вирази 45 – 6 і 28 + 4. Міркуємо так: 1) знаходимо значення першого виразу: 45 – 6 = 39; 2) знаходимо значення другого виразу: 28 + 4 = 32; 3) порівнюємо отримані результати: 39 > 32; 4) робимо висновок: так як 39 > 32, то й 45 – 6 > 28 + 4. Форма запису в зошиті:
Розглянемо другий спосіб порівняння математичних виразів – логічний. Зазначимо, що цей спосіб порівняння математичних виразів був нами запропонований учням ще в 1-му класі.
§ Прочитайте кожний вираз. 5 + 7 – сума чисел 5 та 7; 5 + 9 – сума чисел 5 та 9. § Чим цікаві ці вирази? (Обидва вирази – це суми.) § Що спільного в цих сумах? (В них однакові перші доданки) § Чим вони відрізняються? (В них різні другі доданки). § Зробіть висновок: з двох сум з однаковими першими доданками, менша та, в якій другий доданок менший. Порівнюючи математичні вирази логічним способом ми застосовуємо знання учнів про зміну результатів арифметичних дій в залежності від зміни компонентів. Вчитель повинен пам’ятати, що Наприклад:
(Чим більше відняли від одного й того самого числа, тим менше залишилося)
З двох часток з однаковими дільниками менша та, у якій ділене менше.
З двох часток з однаковими діленими більше та, в якій дільник менший. Можна пропонувати дітям завдання на порівняння математичних виразів двома способами. Наприклад: 2 × 5 > 2 × 2 2 × 5 > 2 × 2 10 > 4 5 > 2 (якщо перші множники однакові, то більший той добуток, у якого другий множник більший) В темі “Табличне множення і ділення” учні знайомляться з третім способом порівняння математичних виразів на підставі перетворення математичного виразу. Наприклад: 2 + 2 + 2 + 2 < 2 × 5 2 × 4 < 2 × 5 Порівнюючи математичні вирази даним способом, ми спочатку виконали тотожне перетворення першого виразу на підставі конкретного змісту дії множення. Тотожні перетворення виразів Тотожні перетворення виразів – це заміна даного виразу іншим, значення котрого рівно значенню даного (зазначимо, що це означення вірно лише для чисел, які вивчаються в курсі початкової школи). Тотожні перетворення в 2-му класі здійснюються на підставі властивостей арифметичних дій та їх наслідків: 1) переставної властивості множення та додавання; 2) сполучної властивості додавання та множення; 3) правил: - віднімання суми від числа, числа від суми:
Вивчаючи властивості арифметичних дій діти впевнюються, що в деяких виразах можна виконувати дії по-різному, але значення їх при цьому не змінюється. Далі знання цих властивостей арифметичних дій учні застосовують для перетворення виразів у тотожні. 48 + 5 = 48 + (2 + 3) = (48 + 2) + 3 = 53 Важливо, щоб учні не тільки пояснювали на підставі чого вони отримають наступний вираз, але й розуміли, що всі ці вирази поєднує знак “=” тому, що вони мають однакові значення. Учні 2-го класу виконують тотожні перетворення не тільки на підставі властивостей арифметичних дій, але й на підставі їх конкретного змісту дії множення: 3 × 4 = 3 + 3 + 3 +3 Буквені вирази Підготовка до ознайомлення із буквою - змінною здійснюється ще в 1-му класі, де широко застосовуються приклади з віконцем. Підготовкою є вся система вправ на складання таблиць додавання й віднімання. При складанні таблиць додавання в межах першого десятку перший доданок змінний, а другий – сталий: £ + 1 У таблицях на віднімання змінним виступає зменшуване, а сталим – від’ємник. Тут доцільною буде така робота: § Ми склали таблицю додавання числа 3.Прочитайте перший приклад з таблиці (1+3=4). Прочитайте другий приклад (2+3=5). Порівняйте ці приклади. Що ви помітили? (В них однакові другі доданки, а перші доданки та суми в них різні) Розглянемо увесь стовпчик прикладів. Що можна сказати про другі доданки, що можна сказати про перші доданки? (Другі доданки у прикладах не змінюються, а перші змінюються від 1 до 7) § Отже, усі випадки таблиці додавання числа 3 можна узагальнити так: £ + 3 § Якщо у “віконце” поступово підставляти числа від 1 до 7, то ми отримаємо усі випадки таблиці. Як підготовчі виступають вправи з віконцем – де у віконце треба підставити число. Ці вправи підводять до поняття “ невідомого числа”: Хто із тварин вірно розв’язав приклад: 3 + £ = 9 Також підготовчими до введення поняття “змінної” служать вправи на склад числа, на доповнення, на збільшення чи зменшення заданих чисел на якесь стале число, різні ігрові вправи та задачі з пропущеними числами. 1. Які числа можна записати у віконцях?: £ + £ = 6 2. Доповнити до 10: 3. У хлопчика було 7 кролів. Він подарував товаришу £ кролів. Скільки кролів залишилося у хлопчика? Також у підручнику є завдання виду: 6 + 3 = £ Ознайомлення. У 2-му класі для позначення змінної використовується буква а, яка має однакову назву в українському та латинському алфавітах. Треба зазначити, що у підручнику Л.П.Кочиної діти вже в 2-му класі знайомляться з буквами латинського алфавіту. Буквене позначення компонента дії додавання вводиться під час вивчення таблиць додавання з переходом через десяток (перед вивченням таблиці додавання числа 5). На першому уроці діти повинні усвідомити, що буквою позначено не одне якесь визначене число, а в загалі будь-яке число. Букві можна надавати різноманітні числові значення. Показати це дітям слід яскраво образно, використовуючи резерви наочно образного мислення та відповідного виду пам’яті молодших школярів, з метою розуміння цього абстрактного поняття та міцного його запам’ятовування. Методика роботи § Розглянемо стовпчик прикладів. 8+1 § Прочитайте перші доданки. 8+2 § Прочитайте другі доданки. 8+3 § Порівняйте в цих прикладах 1-ші та другі доданки. 8+4 § Який доданок сталий? § Який доданок змінюється? § Щоб не записувати змінні - різні числа другого доданка, можна позначити його “віконцем”, але так не зручно, тому в математиці змінну позначають буквою, наприклад а. § Читаємо цей запис так: сума чисел 8 та а або 8 плюс а. § 8+ а – це теж вираз – сума, але не такий які ми розглядали раніш. Чим цей вираз відрізняється від тих виразів, які ми розглядали попереду? § Цей вираз утримує букву поряд з числом, тому він називається буквеним виразом. § Якщо замість букви підставимо вказані числа, то для кожного числа знайдемо суму 8 та а. § Якщо а =1, тоді 8 + а =8 + 1 = 9. § Якщо а =2, тоді 8 + а =8 + 2 = 10 § Таким чином, щоб знайти значення буквеного виразу слід замість букви підставити її значення й обчислити значення числового виразу:
§ Знайдіть самостійно суму 8 та а, якщо а =3, а =4. § Буквою можна позначити не лише другий чи перший доданок, а й зменшуване або від’ємник. Ми розглянули індуктивну методику введення буквених виразів (від часткового до загального. Існує дедуктивна методика (від загального до часткового). Розглянемо її. Припустимо дано вираз: а + в, де а – будь-яке число. Яким може бути перший доданок? (Діти називають свої варіанти.) в – будь-яке число. Яким може бути другий доданок? Щоб знайти значення суми, треба буквам а і в надати значення: 1. Нехай а = 8, в = 7, тоді значення виразу а + в = 8 + 7 = 15; 2. Якщо а = 14, в = 18, то а + в = 14 + 18 = 32; 3. Якщо а = 25, в = 49, то а + в= 25 + 49 = 74. § Які значення може приймати буква “а”? (Будь-які!) § Які значення може приймати буква “в”? (Будь-які!) Розглянемо інший вираз: а – в 1) якщо а = 81, в = 38, то а – в = 81 – 38 = 43; 2) якщо а = 72, в = 47, то а – в = 72 – 47 = 25; 3) якщо а = 68, в = 16, то а – в = 68 – 16 = 52. - а – зменшуване. Які значення може приймати а? (Будь-які!) - в – від’ємник. Які значення може приймати буква “в”? (Будь-які, але не більше, ніж зменшуване!) Обговорюємо ці питання далі: а – в; в Якщо а = 40, то в Якщо а = 34, а в = 40, то різниця не існує в множині натуральних чисел. В подальшому ставиться задача про знаходження значень виразів при заданих значеннях букв. З метою включення вправ на знаходження значень буквених виразів в усну лічбу діти знайомляться з табличною формою завдань на знаходження значень буквених виразів. У процесі виконання завдань на знаходження значень виразів із змінною формується розуміння змінної як букви у виразі, що може набувати деякої множини значень. В учнів має створитися чітке уявлення про те, що у виразу із змінною – буквою не має певного значення, воно залежить від того яке значення приймає буква. Розв’язування задач виразом В 2-му класі вчимо учнів розв’язувати задачі виразом. Розглянемо задачу: У туриста було 10 яблук. На зупинці він з’їв 3 яблука, але в селі купив ще 8 яблук. Скільки яблук стало у туриста? Розглянемо міркування по розв’язуванню цієї задачі: було 10 яблук, 3 яблука з’їв, то в туриста залишилося (10 – 3) яблук; в селі він купив 8 яблук, то у нього стало (10 – 3) + 8 яблук. Обчислюємо значення цього виразу: (10 – 3) + 8 =? + 8 = 15 (ябл.) Відповідь: 15 яблук стало у туриста. Підготовча робота до введення поняття Розглянемо завдання, метою яких є підготовка учнів до ознайомлення з рівняннями та нерівностями із змінною, які, до речі, вводяться в 3-му класі. 1. Підбери потрібні числа, так щоб рівності були вірними: £ – 5 = 7 £ + 5 = 7 § З якого числа треба відняти 5, щоб отримати 7? Відняти 5 – це означає знайти таке число 7, яке в сумі з від’ємником дає зменшуване: 7 + 5 = 12. В квадратик на місті зменшуваного треба поставити число 12.
Розглянемо другий приклад: £ + 5 = 7
2. Підбери такі числа, щоб записи були вірними: 10 + £ < 18 20 – £ > 15 2 × £ > 10 Це завдання розв’язується методом підбору: в першому випадку можна брати будь-які числа від 0 до 7: 10 + £ < 18 10 + 0 < 18 вірно 10 + 1 < 18 вірно 10 + 2 < 18 вірно 10 + 3 < 18 вірно 10 + 4 < 18 вірно 10 + 5 < 18 вірно 10 + 6 < 18 вірно 10 + 7 < 18 вірно 10 + 8 < 18 невірно В другому випадку можна брати числа від 0 до 4. А в третьому - від 6 до нескінченності: 2 × £ > 10 2 × 1 > 10 не вірно 2 × 2 > 10 не вірно 2 × 3 > 10 не вірно 2 × 4 > 10 не вірно 2 × 5 > 10 не вірно 2 × 6 > 10 вірно На прикінці підручника Л.П.Кочиної “Математика 2” пропонується вправа: до невідомого числа додали 12 і отримали 40. Знайди невідоме число. £ + 12 = 40 Аналізуємо рівність: § Що записано ліворуч від знака рівності? (Сума) § Який компонент невідомий? (Перший доданок.) § Як знайти перший доданок? (Треба від суми відняти другий доданок.) § Виконайте дії. § Назвіть чому дорівнює перший доданок. Доведіть це – зробіть перевірку. £ + 12 = 40 £ = 40 – 12
28 + 12 = 40 40 = 40 Аналогічно розв’язується завдання: задумане число зменшили на 20 і отримали 65. Яке число задумали? § Що означає вислів задумане число зменшили на 20? (Від цього числа відняли 20) § Складіть рівність з віконцем. § Який компонент невідомий? § Як знайти невідомий компонент? § Знайдіть невідомий компонент. § Зробіть перевірку. £ – 20 = 65 £ = 65 + 20
85 – 20 = 65 65 = 65 Треба зазначити, що поняття про рівняння в 2-му класі не вводиться, хоча на прикладі таких завдань ми фактично розв’язували рівняння.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2014; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.007 с.) |




 змінюються в одному напрямку: якщо один із
змінюються в одному напрямку: якщо один із 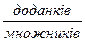 збільшиться
збільшиться  , то й
, то й  теж збільшиться, і навпаки. Так само в одному напрямі змінюються
теж збільшиться, і навпаки. Так само в одному напрямі змінюються  в залежності від зміни
в залежності від зміни  . Але
. Але 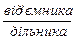 : якщо
: якщо  збільшиться
збільшиться  , то
, то 







 а
а





 £ = 28
£ = 28 £ = 85
£ = 85


