Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраїчний матеріал в курсі математики 2-го класуСтр 1 из 6Следующая ⇒
Порівняння математичних виразів В 2-му класі продовжується робота над порівнянням чисел, числа та виразу, двох математичних виразів. Порівняти математичні вирази – це означає встановити, значення якого виразу більше, менше або вони рівні. Вирази порівнюються декількома способами: 1. Знаходимо значення кожного виразу і порівнюємо отримані числа. Більше той вираз, значення якого більше. І навпаки. 2. Порівнюємо вирази, аналізуючи їх: 3×5 …3×4 - обидва вирази – добутки; в обох добутках однакові перші множники, значить більший той вираз у якого другий множник більший: 5 більш ніж 4,тому 3×5 більше 3×4. 3. Перетворення виразу й порівняння виразів 2-им способом: Розглянемо ці способи докладно. Спочатку учні вчаться порівнювати вираз і число, наприклад: 8 + 5 і 12. Першим кроком знаходимо значення суми: 8 + 5 = 13. Другим кроком порівнюємо отриманий результат з числом 12: 13 > 12. Третім кроком робимо висновок: якщо 13 > 12, то 8 + 5 > 12. Форма запису в зошиті:
Далі порівнюються два математичні вирази. Треба порівняти вирази 45 – 6 і 28 + 4. Міркуємо так: 1) знаходимо значення першого виразу: 45 – 6 = 39; 2) знаходимо значення другого виразу: 28 + 4 = 32; 3) порівнюємо отримані результати: 39 > 32; 4) робимо висновок: так як 39 > 32, то й 45 – 6 > 28 + 4. Форма запису в зошиті:
Розглянемо другий спосіб порівняння математичних виразів – логічний. Зазначимо, що цей спосіб порівняння математичних виразів був нами запропонований учням ще в 1-му класі.
§ Прочитайте кожний вираз. 5 + 7 – сума чисел 5 та 7; 5 + 9 – сума чисел 5 та 9. § Чим цікаві ці вирази? (Обидва вирази – це суми.) § Що спільного в цих сумах? (В них однакові перші доданки) § Чим вони відрізняються? (В них різні другі доданки). § Зробіть висновок: з двох сум з однаковими першими доданками, менша та, в якій другий доданок менший. Порівнюючи математичні вирази логічним способом ми застосовуємо знання учнів про зміну результатів арифметичних дій в залежності від зміни компонентів. Вчитель повинен пам’ятати, що
Наприклад:
(Чим більше відняли від одного й того самого числа, тим менше залишилося)
З двох часток з однаковими дільниками менша та, у якій ділене менше.
З двох часток з однаковими діленими більше та, в якій дільник менший. Можна пропонувати дітям завдання на порівняння математичних виразів двома способами. Наприклад: 2 × 5 > 2 × 2 2 × 5 > 2 × 2 10 > 4 5 > 2 (якщо перші множники однакові, то більший той добуток, у якого другий множник більший) В темі “Табличне множення і ділення” учні знайомляться з третім способом порівняння математичних виразів на підставі перетворення математичного виразу. Наприклад: 2 + 2 + 2 + 2 < 2 × 5 2 × 4 < 2 × 5 Порівнюючи математичні вирази даним способом, ми спочатку виконали тотожне перетворення першого виразу на підставі конкретного змісту дії множення. Буквені вирази Підготовка до ознайомлення із буквою - змінною здійснюється ще в 1-му класі, де широко застосовуються приклади з віконцем. Підготовкою є вся система вправ на складання таблиць додавання й віднімання. При складанні таблиць додавання в межах першого десятку перший доданок змінний, а другий – сталий: £ + 1 У таблицях на віднімання змінним виступає зменшуване, а сталим – від’ємник. Тут доцільною буде така робота: § Ми склали таблицю додавання числа 3.Прочитайте перший приклад з таблиці (1+3=4). Прочитайте другий приклад (2+3=5). Порівняйте ці приклади. Що ви помітили? (В них однакові другі доданки, а перші доданки та суми в них різні) Розглянемо увесь стовпчик прикладів. Що можна сказати про другі доданки, що можна сказати про перші доданки? (Другі доданки у прикладах не змінюються, а перші змінюються від 1 до 7) § Отже, усі випадки таблиці додавання числа 3 можна узагальнити так: £ + 3 § Якщо у “віконце” поступово підставляти числа від 1 до 7, то ми отримаємо усі випадки таблиці. Як підготовчі виступають вправи з віконцем – де у віконце треба підставити число. Ці вправи підводять до поняття “ невідомого числа”: Хто із тварин вірно розв’язав приклад: 3 + £ = 9 Також підготовчими до введення поняття “змінної” служать вправи на склад числа, на доповнення, на збільшення чи зменшення заданих чисел на якесь стале число, різні ігрові вправи та задачі з пропущеними числами.
1. Які числа можна записати у віконцях?: £ + £ = 6 2. Доповнити до 10: 3. У хлопчика було 7 кролів. Він подарував товаришу £ кролів. Скільки кролів залишилося у хлопчика? Також у підручнику є завдання виду: 6 + 3 = £ Ознайомлення. У 2-му класі для позначення змінної використовується буква а, яка має однакову назву в українському та латинському алфавітах. Треба зазначити, що у підручнику Л.П.Кочиної діти вже в 2-му класі знайомляться з буквами латинського алфавіту. Буквене позначення компонента дії додавання вводиться під час вивчення таблиць додавання з переходом через десяток (перед вивченням таблиці додавання числа 5). На першому уроці діти повинні усвідомити, що буквою позначено не одне якесь визначене число, а в загалі будь-яке число. Букві можна надавати різноманітні числові значення. Показати це дітям слід яскраво образно, використовуючи резерви наочно образного мислення та відповідного виду пам’яті молодших школярів, з метою розуміння цього абстрактного поняття та міцного його запам’ятовування. Методика роботи § Розглянемо стовпчик прикладів. 8+1 § Прочитайте перші доданки. 8+2 § Прочитайте другі доданки. 8+3 § Порівняйте в цих прикладах 1-ші та другі доданки. 8+4 § Який доданок сталий? § Який доданок змінюється? § Щоб не записувати змінні - різні числа другого доданка, можна позначити його “віконцем”, але так не зручно, тому в математиці змінну позначають буквою, наприклад а. § Читаємо цей запис так: сума чисел 8 та а або 8 плюс а. § 8+ а – це теж вираз – сума, але не такий які ми розглядали раніш. Чим цей вираз відрізняється від тих виразів, які ми розглядали попереду? § Цей вираз утримує букву поряд з числом, тому він називається буквеним виразом. § Якщо замість букви підставимо вказані числа, то для кожного числа знайдемо суму 8 та а. § Якщо а =1, тоді 8 + а =8 + 1 = 9. § Якщо а =2, тоді 8 + а =8 + 2 = 10 § Таким чином, щоб знайти значення буквеного виразу слід замість букви підставити її значення й обчислити значення числового виразу:
§ Знайдіть самостійно суму 8 та а, якщо а =3, а =4. § Буквою можна позначити не лише другий чи перший доданок, а й зменшуване або від’ємник. Ми розглянули індуктивну методику введення буквених виразів (від часткового до загального. Існує дедуктивна методика (від загального до часткового). Розглянемо її. Припустимо дано вираз: а + в, де а – будь-яке число. Яким може бути перший доданок? (Діти називають свої варіанти.) в – будь-яке число. Яким може бути другий доданок? Щоб знайти значення суми, треба буквам а і в надати значення: 1. Нехай а = 8, в = 7, тоді значення виразу а + в = 8 + 7 = 15; 2. Якщо а = 14, в = 18, то а + в = 14 + 18 = 32; 3. Якщо а = 25, в = 49, то а + в= 25 + 49 = 74. § Які значення може приймати буква “а”? (Будь-які!) § Які значення може приймати буква “в”? (Будь-які!) Розглянемо інший вираз: а – в 1) якщо а = 81, в = 38, то а – в = 81 – 38 = 43; 2) якщо а = 72, в = 47, то а – в = 72 – 47 = 25; 3) якщо а = 68, в = 16, то а – в = 68 – 16 = 52. - а – зменшуване. Які значення може приймати а? (Будь-які!) - в – від’ємник. Які значення може приймати буква “в”? (Будь-які, але не більше, ніж зменшуване!)
Обговорюємо ці питання далі: а – в; в Якщо а = 40, то в Якщо а = 34, а в = 40, то різниця не існує в множині натуральних чисел. В подальшому ставиться задача про знаходження значень виразів при заданих значеннях букв. З метою включення вправ на знаходження значень буквених виразів в усну лічбу діти знайомляться з табличною формою завдань на знаходження значень буквених виразів. У процесі виконання завдань на знаходження значень виразів із змінною формується розуміння змінної як букви у виразі, що може набувати деякої множини значень. В учнів має створитися чітке уявлення про те, що у виразу із змінною – буквою не має певного значення, воно залежить від того яке значення приймає буква. Розв’язування задач виразом В 2-му класі вчимо учнів розв’язувати задачі виразом. Розглянемо задачу: У туриста було 10 яблук. На зупинці він з’їв 3 яблука, але в селі купив ще 8 яблук. Скільки яблук стало у туриста? Розглянемо міркування по розв’язуванню цієї задачі: було 10 яблук, 3 яблука з’їв, то в туриста залишилося (10 – 3) яблук; в селі він купив 8 яблук, то у нього стало (10 – 3) + 8 яблук. Обчислюємо значення цього виразу: (10 – 3) + 8 =? + 8 = 15 (ябл.) Відповідь: 15 яблук стало у туриста. Підготовча робота до введення поняття Розглянемо завдання, метою яких є підготовка учнів до ознайомлення з рівняннями та нерівностями із змінною, які, до речі, вводяться в 3-му класі. 1. Підбери потрібні числа, так щоб рівності були вірними: £ – 5 = 7 £ + 5 = 7 § З якого числа треба відняти 5, щоб отримати 7? Відняти 5 – це означає знайти таке число 7, яке в сумі з від’ємником дає зменшуване: 7 + 5 = 12. В квадратик на місті зменшуваного треба поставити число 12.
Розглянемо другий приклад: £ + 5 = 7
2. Підбери такі числа, щоб записи були вірними: 10 + £ < 18 20 – £ > 15 2 × £ > 10 Це завдання розв’язується методом підбору: в першому випадку можна брати будь-які числа від 0 до 7: 10 + £ < 18 10 + 0 < 18 вірно 10 + 1 < 18 вірно 10 + 2 < 18 вірно 10 + 3 < 18 вірно 10 + 4 < 18 вірно 10 + 5 < 18 вірно 10 + 6 < 18 вірно 10 + 7 < 18 вірно 10 + 8 < 18 невірно В другому випадку можна брати числа від 0 до 4. А в третьому - від 6 до нескінченності: 2 × £ > 10 2 × 1 > 10 не вірно 2 × 2 > 10 не вірно 2 × 3 > 10 не вірно 2 × 4 > 10 не вірно 2 × 5 > 10 не вірно 2 × 6 > 10 вірно На прикінці підручника Л.П.Кочиної “Математика 2” пропонується вправа: до невідомого числа додали 12 і отримали 40. Знайди невідоме число.
£ + 12 = 40 Аналізуємо рівність: § Що записано ліворуч від знака рівності? (Сума) § Який компонент невідомий? (Перший доданок.) § Як знайти перший доданок? (Треба від суми відняти другий доданок.) § Виконайте дії. § Назвіть чому дорівнює перший доданок. Доведіть це – зробіть перевірку. £ + 12 = 40 £ = 40 – 12
28 + 12 = 40 40 = 40 Аналогічно розв’язується завдання: задумане число зменшили на 20 і отримали 65. Яке число задумали? § Що означає вислів задумане число зменшили на 20? (Від цього числа відняли 20) § Складіть рівність з віконцем. § Який компонент невідомий? § Як знайти невідомий компонент? § Знайдіть невідомий компонент. § Зробіть перевірку. £ – 20 = 65 £ = 65 + 20
85 – 20 = 65 65 = 65 Треба зазначити, що поняття про рівняння в 2-му класі не вводиться, хоча на прикладі таких завдань ми фактично розв’язували рівняння. Кут. Прямий кут Прямокутник Пропонуємо набір геометричних фігур й засобом виключення зайвих фігур залишаємо фігури, що вивчаються.
§ Уважно розгляньте фігури. Яку фігуру можна виключити? Чому? § Як одним словом можна назвати решту фігур? (чотирикутники) § Знайдіть чотирикутник, у якого немає прямого кута (за допомогою креслювального трикутника). (2, 3) § Знайдіть чотирикутник, у якого є тільки один прямий кут (1). Виключимо його, що можна сказати про решту чотирикутників? (в цих чотирикутниках більш ніж один прямий кут). § Знайдіть чотирикутник, у якого тільки два прямих кута (4). Виключимо його, що можна сказати про решту чотирикутників?(в цих чотирикутниках більш ніж два прямих кута). § Що можна сказати про решту чотирикутників? (5, 6, 7) Скільки в них прямих кутів? (в них всі кути прямі!) § Такі фігури називаються прямокутниками. Вводимо означення фігури: (родове поняття – чотирикутник, видове поняття – прямі кути) Означення: чотирикутник, у якого всі кути прямі називається прямокутником. Ілюстрація: знайдіть у оточуючій обстановці предмети прямокутної форми. § Покажіть прямокутники серед геометричних фігур. § Виріжте з паперу в клітинку прямокутник. Властивості: Дітям пропонується набір геометричних фігур, які вирізані з аркушу: § Візьміть в руки прямокутник. Порівняйте за довжиною його протилежні сторони – ті, що лежать напроти одна одної. Використовуйте прийом накладання. § Що цікавого ви помітили? (у прямокутника протилежні сторони попарно рівні). § Перевіримо це ствердження таким чином: виміряйте та запишіть довжину кожної сторони синього прямокутника (у кожного учня різні сині прямокутники). § Назвіть отримані результати вимірювання (вчитель їх записує на дошці)Уважно подивіться на результати вимірювання. Який можна зробити висновок? (у прямокутника протилежні сторони рівні) § Візьміть червоний прямокутник (червоні прямокутники – різні квадрати).Виміряйте довжину його сторін й назвіть отримані результати (вчитель записує їх на дошці).
§ Що цікавого ви помітили? (є такі прямокутники, у котрих не тільки по дві протилежні сторони рівні, а ще є й такі, у яких всі сторони рівні, але взагалі про них теж можна сказати, що в них протилежні сторони рівні.) Задачі на побудову. Квадрат Пропонуємо набур геометричних фігур й засобом виключення зайвих фігур залишаємо фігури, що вивчаються. § Які фігури зображено на малюнку? (прямокутники) § Виміряйте сторони прямокутників. Чи треба виконувати чотири вимірювання? Чому? § Що цікавого ви помітили?(серед прямокутників знаходяться й такі, у яких всі сторони рівні між собою) § Такі прямокутники називаються квадратами. Вводимо означення фігури: Означення: прямокутник, у якого всі сторони рівні називається квадратом. Тобто квадрат – це взагалі прямокутник, але не звичайний, а такий що має усі рівні сторони (Родове поняття прямокутник, а видове – всі сторони рівні). Ілюстрація; Властивості: всі сторони рівні і всі кути рівні. § Покажи прямокутники, які не можна назвати квадратами. § Про кожний квадрат можна сказати, що він прямокутник. Чи можна, навпаки, про кожний прямокутник сказати, що він квадрат? § Домалюй цю фігуру, щоб отримати квадрат. Задачі на побудову. Коло. Круг § Серед геометричних фігур є круги (вчитель показує модель круга).Багато предметів мають форму круга. Назвіть такі предмети. § Як можна зобразити круг на папері? (взяти й обвести блюдце й тощо).Але це незручно, адже круги потрібні різні. Для цього користуються інструментом – циркулем. § Візьміть циркуль. Поставимо першу ніжку (з гострим кінцем) на аркуш паперу – це буде центр кола, а другою ніжкою циркуля опишімо круг. Ми отримали коло. Лінія, яку креслить циркуль, називається колом. Коло є межею круга. З чого можна зробити модель кола? (з ниток, дроту) З чого можна зробити модель круга? (вирізати з паперу й тощо) У круга есть одна подруга, Знакома всем ее наружность! Она идет по краю круга И назвается – окружность. § Коли ми креслимо коло циркулем, то його голка повинна весь час знаходитися в одній точці – центрі кола. Тепер поставимо на колі дві будь-які дві точки й з’єднаємо їх почергово з центром кола. Виміряйте довжину отриманих відрізків. Назвіть результати вимірювання.(вчитель записує їх на дошці).Уважно розгляньте отримані результати вимірювання. Що цікавого ви помітили?(у кожному випадку вимірювання відрізки є рівними) § Який можна зробити висновок? (якщо ми з’єднаємо центр кола з будь якими точками на колі, то ми отримаємо рівні відрізки) Відрізки, що з’єднують центр кола з будь-якою точкою кола називаються радіусами кола. Радіус – це відрізок, який з’єднує центр кола з будь-якою точкою кола. У підручнику центр кола позначається буквою О, а радіус – ОА. Можливі вправи: 1) покажи 2 круга різного кольору; різного радіусу (серед кількох на дошці). Який з них більший – зелений чи червоний? У якого круга радіус більший?
2) у цих кіл спільний центр. Накреслити кілька кіл з спільним центром. Де в навколишньому світі ви зустрічали кілька кіл з спільним центром (круги на воді після падіння каменя). 3) побудуй коло, проведи в ньому радіус; скільки радіусів можна провести? 4) накреслити коло з радіусом 2 см. Робота над завданням 1. Малюємо ескіз від руки й намітимо шляхи розв’язання: 2. Будуємо за допомогою циркуля та лінійки: - креслимо відрізок довжиною 2 см; - встановлюємо ніжки циркуля на кінці цього відрізку; - проводимо коло, відмічаємо центр кола. 3. Доведення: проводимо радіус отриманого кола, вимірюємо його. Отримали – 2 см. Тому ми побудували коло, що вимагалося. 4. Дослідження: якщо б ми не задали довжину радіусу – 2 см, а просто б попросили накреслити коло, скільки б було розв’язків? (багато). - Ми побудували коло з радіусом 2 см. Тепер розмалюйте круг з цим же радіусом. Відмітимо точки, що лежать у крузі та поза кругом, на колі. Довжина При закругленні одиниць вимірювання довжини – сантиметра та дециметра та співвідношення між ними, дітям пропонується перевести просте іменоване число у складене: 14 см = 1дм 4 см. Тут міркування здійснюються таким чином: число 14 містить 1десяток та 4 окремі одиниці; в 14 см міститься 10 см та ще 4 см, 10 см – складають 1 дм, тому в 14 см міститься 1 дм і 4 см. Учні виконують обернені завдання: перевести складене іменоване число у просте: 2 дм 4 см = 24 см. При виконанні цього завдання міркуємо так: в 1 дм – 10 см, в 2 дм – в двічі більше, 20 см; 20 см та 4 см, буде 24 см. Поступово учні усвідомлюють, що числове значення довжини залежить від вибору одиниць вимірювання. Також виконуються вправи: 1. На порівняння іменованих чисел, одне з яких є складеним або обидва числа складені іменовані числа: 4 дм 8 см > 39 см 5 дм 7 см < 5 дм 9 см 48 см > 39 см 57 см < 59 см 2. На знаходження суми та різниці іменованих чисел:
3. На порівняння виразів: 10 дм – 3 дм... 6 дм 8 дм... 4 дм + 3 дм 6 дм + 2 дм... 7 дм + 1 дм 4 см + 5 см... 4 дм + 5 дм Під час вивчення нумерації чисел від 21 до 100 учні знайомляться з новою одиницею вимірювання довжини – 1 метром. Введення нової одиниці вимірювання довжини треба мотивувати. Так учням пропонується виміряти довжину класної кімнати і вони впевнюються, що застосувати попередню мірку – дециметр – не зручно. Згадуємо, як ми міркували, коли нам було не зручно користуватися для вимірювання міркою – 1 см. Ми обрали за одиницю вимірювання довший відрізок, який містив 10 см і назвали його дециметром. В цьому випадку робимо те ж саме: обираємо за мірку довший відрізок, який містить 10 дм. Учні викладають в рядок 10 моделей дециметрів і до цього рядку прикладають частину швейного сантиметру (100 см) - це нова мірка – 1 метр. Отже діти і “відчувають” цю мірку – отримують конкретні уявлення по 1 метр. Розглядаючи модель метру діти підраховують число сантиметрів, які вона містить, і встановлюють, що 1 метрі 100 см. Отже складається таблиця співвідношення одиниць вимірювання довжини: Довжина
Потім модель 1 метру використовуються для вимірювання довжини дошки, довжини класної кімнати й тощо. Якщо на довжині не укладається число метрів, то ми застосовуємо й інші одиниці вимірювання довжини: 1 дм та 1 см. В результаті таких вимірювань отримуємо складені іменовані числа. Далі учням пропонуються завдання: 1. Замінити крупні одиниці вимірювання довжини дрібними: 1 м 6 дм =... дм; 7 м 1 дм =... дм; 65 дм =... м... дм; 80 дм =... м При виконанні цього завдання учні міркують так: 1 м 6 дм – це 1 м та 6 дм; 1 м = 10 дм; маємо 10 дм і ще 6 дм, всього 16 дм. В даному числі стільки десятків, скільки метрів у іменованому числі, і стільки одиниць, скільки окремих дециметрів. 7 м 1 дм. В даному числі дециметрів буде стільки десятків, скільки метрів – 7 (1м = 10 дм), і стільки одиниць, скільки окремих дециметрів – 1. Маємо 7 м 1 дм = 71 дм. 65 дм. 10 дм складають 1 м, тому метрів буде стільки, скільки в цьому числі десятків – 6 м, а дециметрів стільки, скільки одиниць – 5 дм. 65 дм = 6 м 5 дм. 2. Записати в сантиметрах: 2 дм 8 см 1 м 9 дм 9 см 8 дм 2 см 10 дм 7 дм 3. Замінити крупні одиниці вимірювання дрібни і навпаки: 70 см =... дм 3 дм 8 см =... см 2 дм =... см 41 см =.... дм... см 4. Порівняти іменовані числа: 4 м 8 дм > 39 дм 5 м 7 дм < 5 м 9 дм 48 дм > 39 дм 57 дм < 59 дм 1. На знаходження суми та різниці іменованих чисел:
2. На порівняння виразів: 11 м – 3 м... 6 м 18 м... 9 м + 8 м 6 м + 7 м... 7 м + 5 м 6 м + 5 м... 4 м + 7 м Маса В 2-му класі не вводиться нових одиниць вимірювання маси. Одиниця вимірювання маси – кілограм, застосовується при додаванні та віднімання, порівнянні іменованих чисел, а також у задачах. Наприклад: Обчисли:
Якщо терези знаходяться у рівновазі, тоді маси предметів рівні. Якщо рівновагу порушено, то маса предмету на нижній чаші більше маси предмета на верхній чаші і навпаки. Порівняй маси предметів:
 
Треба включати розв’язування задач, які відтворюють процес зважування, наприклад: «На одній чашці терезів стоїть ящик з яблуками, а на другій – дві гирі по 5 кг. Терези знаходяться в рівновазі. Яка маса ящика з яблуками?» Крім того, підручник містить задачі, в яких використані одиниці вимірювання маси. Час За програмою в 2-му класі вивчаються одиниці вимірювання часу: доба, тиждень, місяць, рік. Учителю треба вірно формувати уявлення учнів про одиниці вимірювання часу, як про конкретні проміжки часу. Доба – проміжок часу, протягом якого Земля робить повний оберт навколо своєї осі (Демонструємо це на глобусі). Можна повідомити учням, що доба ділиться на 24 рівні частини – години. Доба містить 24 години. Підрахунок доби починається опівночі. Формуючи уявлення про добу спираємося на близькі дітям спостереження: від початку занять сьогодні до початку занять завтра пройде одна доба. Доба – це ранок, день, вечір, ніч. При цьому важливо уточнити уявлення, які пов’язані з термінами “вчора”, “позавчора”, “завтра”, “сьогодні”, “післязавтра”. Пропонуємо дітям розповісти, що вони робили вчора, сьогодні, що збираються робити завтра, який сьогодні день тижня, яке число, яке число буде завтра, яке було вчора... Тиждень – це проміжок часу, якій містить 7 діб. Діти засвоюють дні тижня: понеділок, вівторок, середа, четвер, п’ятниця, субота, неділя. Приблизно чотири тижні складають один місяць. Місяць – це проміжок часу, протягом якого Місяць робить повний оберт навколо Землі та навколо своєї вісі. Період руху Місяця навколо своєї вісі та період руху Місяця навколо Землі співпадають, тому ми бачимо Місяць весь час з однієї сторони. Місяць містить трошки менше 30 діб. Тому місяць містить від 28 до 31 діб. Рік – це проміжок часу, протягом якого Земля робить повний оберт навколо Сонця (показуємо це на астрономічному приладі – телурії). Рік містить 365 діб та 6 годин. Тому домовилися вважати 3 роки по 365 діб кожний, а четвертий – по 366 діб і його називати високосним. Останній високосний рік був в 2000 році, а наступний буде в 2004 році. За час, який Земля робить повний оберт навколо Сонця, Місяць робить 12 повних обертів навколо Землі. Тому, рік поділяють на 12 проміжків – місяців. Рік містить 12 місяців. Уточнення уявлень про рік, місяць, тиждень проходить на основі практичних вправ, які вимагають застосування табель-календаря (3-й клас). Діти під керівництвом учителя складають табель-календар на той чи інший місяць. Розглядаючи календар, діти краще уявляють собі, як багато днів в році, скільки в році місяців, в якій послідовності вони йдуть друг за другом, скільки днів в місяці. Працюючи з табель-календарем звертаємо увагу на число днів в кожному місяці, виписуємо та запам’ятовуємо місяці, в яких 30 днів (таких місяців всього чотири: квітень, червень, вересень, листопад). Крім того, формуючи уявлення про рік спираємося на близькі дітям спостереження: від святкування дня народження до наступного святкування пройде один рік, від святкування Нового року до наступного святкування пройде один рік... Діти розв’язують задачі, які містять іменовані числа, подані в одинцях вимірювання часу, наприклад: Дідусі Максиму – 71 рік, бабусі Вірі – 68 років, батькові – 41 рік, матері – 35 років, а мені 7 років. Хто найстарший, хто наймолодший? Вартість Це найближча до сприйняття дітей величина. Майже усі діти виконують доручення, купуючи продукти в магазині, тому ознайомлення з одиницями вартості – копійкою та гривнею, витікає з потреб повсякденного життя. При вивченні нумерації чисел в межах 100, діти знайомляться з одиницею вимірювання вартості 1 гривнею, і засвоюють:
Діти знайомляться з різними монетами: 50 к, 25 к, 10 к, 5 к, 2 к, 1 к. В 2-му класі учні розв’язують задачі, які містять іменовані числа, подані в одиницях вартості, наприклад: “У хлопчика було 72 копійки. Він витратив на булочку 27 копійок і на бублик 35 копійок. Скільки грошей залишилося у хлопчика?”. Можна розглянути ще й таку задачу: “За три книги сплатити 8 грн. Одна книжка коштує 2 гривні, а друга 3 гривні. Скільки коштує третя книжка?” § Склади короткий запис задачі. § Запиши розв’язання і відповідь.
ЦІКАВІ ЗАВДАННЯ ТА ЗАВДАННЯ Числові магічні квадрати Істинне і помилкове висловлювання. Думки 5. Чи вірні такі думки? § Вітер віє, бо дерева качаються. § Якщо тротуар мокрий, то пройшов дощ. § Придумай початок речення. § Якщо …, то я піду на прогулянку. § Якщо …, то на небі веселка. § Ми …, тому що пішов дощ. 6. Закінчи речення. § Якщо пройшов дощ, то… § Якщо взимку буде сильна стужа, то… § Сашко захворів, в нього піднялася температура, бо… 7. Встанови, чи істині або хибні думки. § Якщо у чотирикутника всі кути прямі, то це квадрат. § Якщо у чотирикутника всі сторони рівні, то це квадрат. Перетвори ці думки так, щоб вони були вірними. 8. Чи вірне таке судження: § Якщо від суми однакових доданків відняти один з них, то отримуємо другий доданок. Доведи свою думку за допомогою математичних прикладів. Умовиводи 1. Вася помітив, що дерев’яна палка плаває, дерев’яна човен плаває, колода плаває. Який висновок він зробив? Чи згоден ти з висновком, що усі дерев’яні предмети плавають? 2. Чи вірними будуть такі умовиводи? § Усі кішки мають 4 ноги. Собака теж має 4 ноги. Значить собака – кішка? § Усі птахи мають крила. Страус – це птах. Значить страус має крила. § А чому тоді страус не літає? Чи можеш ти відповісти на це питання? 3. Чи вірні міркування? § Якщо усі квадрати є прямокутниками, то деякі прямокутники не є квадратами. § Якщо усі прямокутники є чотирикутниками, то деякі чотирикутники є прямокутниками. § Якщо усі трикутники є геометричними фігурами, то усі геометричні фігури є трикутниками. Виправ невірні міркування так, щоб вони стали вірними. 4. Чи вірне міркування? § Якщо подана сума однакових доданків, то її можна замінити множенням. Якщо подана сума, в якій доданки не однакові, то її не можна замінити множенням. 6. З Чи вірні висновки зроблені з поняття “квадрат”? 1) це прямокутник; 2) всі сторони рівні; 3) всі кути прямі; 4) це чотирикутник; 5) має чотири кути, чотири сторони, чотири вершини. 16. Надя та Катерина були одягнуті у червоне та зелене плаття. Катерина була одягнена не у зелене плаття. У яке плаття одягнена Надя? Як ти це встановив? Логічні задачі, 1. Прочитай задачу. Таня, Катерина та Олена пішли на річку. Підпиши імена дівчат, якщо Таня вища за Катю, я Катя вища за Олену. § Про що говориться у задачі? Що нам відомо про зріст дівчат? Намалюй два кружечки, неоднакові за розміром, що будуть позначати дівчат. Що нам відомо про зріст Тані? Який кружечок підпишемо її ім’ям, маленький чи великий? Чому? Підпиши другий кружечок. Яке ім’я там буде написане? § Що нам відомо про зріст Олени? Чи вона нижча або вища за Катерину? § Яким кружечком позначимо Олену, більшим чи меншим? Чому? Поглянь на свій малюнок та назви імена дівчат у порядку збільшення їхнього зросту. 2. Розв’яжи задачу. Коля стоїть ліворуч від Тані, а Таня стоїть ліворуч від Дими. Як звуть дітей?
§ Уважно прочитай задачу та скажи, про що в неї говориться? Скільки хлопчиків у задачі? А дівчаток? Можна одразу визначити, як звуть дівчину? Як? Підпиши її ім’я. Що відомо про Колю? Можна визначити, хто з хлопчиків Коля? Підпиши його ім’я під малюнком. Хто залишився? 3. Склади схожі задачі, де треба порівняти дітей за зростом, кольором волосся, за товщиною. 4. Гучним голосом серед звірів відмічаються бегемот, лев та крокодил. Хто з них кричить гучніше за всіх, якщо голос бегемота гучніший за рик лева, але тихіший за рик крокодила? Якщо ти не можеш визначити, подумай, з якого звіра треба почати. (Почни з бегемота) 5. На день народження Катерини купили коробку кольорових кульок. У коробці є 5 червоних та 5 синіх кульок. Яку найменшу кількість кульок треба дістати з коробки, щоб узяти кульки різних кольорів? § Про що говориться у задачі? Скільки у коробці червоних кульок? А синіх? Намалюй ці кільки у коробці. Як ти вважаєш, якщо взяти, наприклад 4 кульки, може статися, що усі вони будуть червоні? Чому? А сині? § А якщо взяти 5 кульок, чи можуть вони бути одного кольору? Чому? Скільки кульок треба взяти, щоб серед них була б хоч одна другого кольору? Так, 6. А чому не можна взяти менше? Тобто можна зробити висновок, що треба брати більше кульок, ніж є одного кольору. 6. У шафі стоять три пар черевик. Скільки черевик треба узяти, щоб можна було добрати серед них пару? § Про що говориться у задачі? Скільки пар черевиків? А скільки черевиків? Намалюй їх. Уважно подивись на малюнок. Скільки різних пар черевиків? Тобто, скільки черевиків треба взяти, щоб могли попастися черевики від усіх пар? Так, три. А Скільки їх треба взяти ще, щоб можна було зібрати пару? Вірно, ще один. Так Скільки усього черевиків треба взяти? 7. Склади сам подібну задачу, намалюй до неї малюнок та запропонуй другові її розв’язати. 8. У бабусі живуть кролики та качки. Скільки всього кроликів та качок живе у бабусі, якщо всього в них 10 голів та 28 ніг?
§ Про що говориться у задачі? По скільки голів має кожна тварина? Намалюй 10 кружечків (голів). А по скільки ніг є у качок? А у кроликів? Порівняй кількість голів у тварин. А кількість ніг? У кого ніг більше? Яке найменше число ніг є у кожній тварини? Тобто у тварин повинно бути не менше за дві ноги. Додай до кожного кружечка по дві палички-ноги. § Скільки ніг ти намалював? (20). Скільки ніг всього у тварин? (28). Скільки ніг ще треба домалювати? (8). По скільки ніг треба домалювати, що отримати кролика? Домалюй ще 8 ніг по дві ноги кожній тварині.
§ Скільки кроликів та качок живуть у бабусі? 9. Птахи та звірі заспорили, кого у лісі живе більше. Щоб перевірити це, вони розбилися на однакові групи. У кожній групі очутилося по 8 голів та 24 ноги. Визнач, кого у лісі більше, звірів чи птахів. § Уважно прочитай умову задачі. Про що у ній говориться? § Порівняй звірів та птахів за кількістю ніг та голів. Що ти помітив? § Чи можна визначити, скільки усього звірів було у кожній групі? Намалюй стільки кружечків, скільки звірів у кожній групі. § По скільки ніг є і у птахів, і у звірів? (2) Домалюй до кожного кружечка по 2 палички. § Скільки ніг ми використали? (16) Скільки ще залишилося? По скільки ніг треба ще домалювати до кружечка, щоб отримати звіря? Поділи залишившися 8 ніг між кржечками, домальовуючи до кожного по 2 палички.
§ Скільки кружечків із двома паличками отримали? § Скільки кружечків з 4 паличками? § Скільки птахів у кожній групі? § Скільки звірів у кожній групі? § Кого більше? § Якщо відомо, що усі групи однакові, який можна зробити висновок про кількість птахів та звірів у лісі? 10. Самостійно розв’яжи таку задачу: На дитячому майдані гралися діти. Дівчата гралися з колясками, а хлопчики з трьохколесними велосипедами. Всього колясок та велосипедів було 10. Скільки було на майдані колясок та скільки було велосипедів, якщо усього в них було 33 колеса? (Підказка: визнач, скільки коліс повинно бути, якщо на майдані усі коляски). Задачі, що розв’язуються 1. Уважно прочитай задачу.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.127.141 (0.217 с.) |



 змінюються в одному напрямку: якщо один із
змінюються в одному напрямку: якщо один із 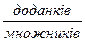 збільшиться
збільшиться  , то й
, то й  теж збільшиться, і навпаки. Так само в одному напрямі змінюються
теж збільшиться, і навпаки. Так само в одному напрямі змінюються  в залежності від зміни
в залежності від зміни  . Але
. Але 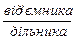 : якщо
: якщо  збільшиться
збільшиться  , то
, то 



 а
а





 £ = 28
£ = 28 £ = 85
£ = 85