
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття про фігури силогізму
Категоричний силогізм має різні види, котрі набули назви фігур силогізму. Фігурами силогізму називаються форми силогізму, що відрізняються одна від одної розташуванням середнього терміна в засновках. Існує чотири фігури силогізму. У першій фігурі середній термін займає місце суб'єкта у більшому засновку і предиката — в меншому. Схема першої фігури: М—Р S-M У другій фігурі середній термін займає місце предиката в обох засновках. Схема другої фігури: Р—М S-M У третій фігурі середній термін займає місце суб'єкта в обох засновках. Схема третьої фігури: M-P M-S У четвертій фігурі середній термін займає місце предиката у більшому засновку і суб’єкта в меншому засновку. Схема P-M M-S 44. Перша фігура силогізму має такі особливі правила: 1. Більший засновок має бути судженням загальним; 2. Менший засновок — судженням ствердним. Перша фігура силогізму — це найтиповіша, класична форма дедуктивного умовиводу, її модуси AAA та ЕАЕ, котрі виражають у чистому вигляді аксіому силогізму, є типовими формами підведення часткового випадку під загальне положення. Друга фігура силогізму має такі правила: 1. Більший засновок має бути судженням загальним; 2. Один Із засновків — судження заперечне. Друга фігура силогізму має такі модуси: ЕАЕ, АЕЕ, ЕІО, АОО. Третя фігура має таке правило: менший засновок має бути ствердним. Висновок у третій фігурі завжди частковий. Третя фігура має такі шість модусів: ААІ, EAOt ІАІ, ОАО, AII, ЕIO. У четвертій фігурі діють такі правила: 1. Якщо більший засновок ствердний, то менший має бути загальним. 2. Якщо один Із засновків заперечний, то більший засновок буде загальним. Четверта фігура має такі п’ять модусів: AAI, АEE, ІАІ, ЕАО,ЕІО. 45. Якщо принаймні одним із засновків категоричного силогізму є виділяюче судження, то такий силогізм є виключенням із загальних правил та особливих правил фігур категоричного силогізму. Порушуючи згадані правила такі силогізми дають необхідні виводи. Модуси таких силогізмів називають слабкими модусами, оскільки вони не завжди дають необхідні виводи, а лише при умові, що принаймні один із засновків силогізму є виділяючим судженням. 1) Вивід з двох часткових суджень, що порушує загальне правило засновків силогізму: “Принаймні один із засновків силогізму повинен бути загальним судженням”. 2) Вивід за І-ою фігурою, коли більший засновок – часткове судження. Це порушує правило І-ої фігури: “Більший засновок повинен бути загальним судженням”. 3) Вивід, в якому один із засновків часткове судження, а висновок - загальне судження. Це порушує загальне правило засновків силогізму: “Якщо один із засновків часткове судження, то і висновок повинен бути частковим судженням”. 4) Вивід за другою фігурою з двох стверджувальних засновків. Це порушує правило другої фігури: “Один із засновків повинен бути заперечним судженням”. 5) Вивід за першою фігурою, в якому менший засновок – заперечне судження. Це порушує правило першої фігури: “Менший засновок повинен бути стверджувальним судженням”. 46 Міркування умови і висновки яких є судженнями з відношенням називають МІРКУВАННЯ З ВІДНОШЕНЯМ. Структура XPY. Логічна основа виведення суджень з відношенням – властивості цих відношень. Є такі властивості 1 ( 2( 3( 4( 5( 6(
47. Умовно-категоричним називається умовивід, у якому одна з посилок - умовне, а інша посилка і висновок - категоричні судження. 48. Розділово-категоричним називається умовивід, у якому одна з посилок - розділову, а інша посилка і висновок - категоричні судження. Прості судження, з яких складається розділове (диз'юнктивне) судження, називаються членами диз'юнкції, або диз'юнктів. Стверджуючи один член диз'юнкції, заперечують інший і, заперечуючи один з них, - стверджують інший. У відповідності з цим розрізняють два модуси розділово-категоричного умовиводу: (1) стверджуючи-заперечливий і (2) заперечливо-стверджуючий. 1. У стверджуючи-заперечливому модусі (modus ponendo tollens) менша посилка - категоричне судження - стверджує один член диз'юнкції, висновок - також категоричне судження - заперечує інший її член. 2. У заперечливо-стверджуючому модусі (modus tollendo ponens) менша посилка заперечує один диз'юнктів, висновок стверджує інший.
49, Умовно-розділове міркування — це міркування, один із засновків якого є диз'юнктивним висловлюванням, а інші засновки — імплікативними висловлюваннями. Розрізняють різні види умовно-розділових міркувань. Так, за кількістю альтернатив у диз'юнктивному засновку умов но-розділові міркування поділяються на: дилеми (дві альтернативи); трилеми (три альтернативи); полілеми (чотири і більше альтернатив). На практиці найчастіше за все застосовують дилеми. Дилеми можна поділити за двома основами:за характером висновку; за складом висновку За характером висновку усі дилеми поділяються на:конструктивны (у висновку якої щось стверджується); деструктивні (у висновку якої щось заперечується). За складом висновку усі дилеми поділяються на: прості(висновок якої є простим висловлюванням або його запереченням.);складні(висновок якої є складним (диз'юнктивним) висловлюванням). На підставі цього поділу у логіці наводиться об'єднана класифікація умовно-розділових міркувань (дилем). Відповідно до неї вони поділяються на такі види: прості конструктивні дилеми(A->C, B->D, AvB / CvD); складні конструктивні дилеми; (A->C, B->D, AvB / CvD); прості деструктивні дилеми; (A->B, A~C, ~Bv~C / ~A)’; кладні деструктивні дилеми. (A->B, C->D, ~Bv~D / ~Av~C) 50. Силогізм з пропущеної посилкою або укладенням називається скороченим силогізмом, або ентимемою. Широко використовуються ентимеми простого категоричного силогізму, особливо висновки по першій фігурі. В залежності від того, яка частина силогізму пропущена, розрізняють три види ентимеми: з пропущеної більшої посилкою, з пропущеної меншою посилкою і з пропущеним висновком. Умовивід у формі ентимеми може бути побудоване і по 2-й фігурі; по 3-й фігурі воно будується рідко. Форму ентимеми приймають також умовиводи, посилками яких є умовні і розділові судження. 51. У процесі міркування прості силогізми виступають в логічному зв'язку один з одним, утворюючи ланцюг силогізмів, в якій висновок попереднього силогізму стає посилкою подальшого. Попередній силогізм називається проашогізмом, наступний - епісімогізмом. З'єднання простих сі.іогізмов, в яка висновок попереднього силогізму (просіллогізма) стає посилкою подальшого сі.глогізма (епісі.іогізма), називається складним силогізмів, або полисиллогизм. Розрізняють прогресивний і регресивний полисиллогизм. У прогресивному полисиллогизм висновок просіллогізма стає більшою посипанням епісіллогізма В регресивному полісі.гюгізме висновок просіллогізма стає меншою посилкою епісіллогізма.
52.Логіка висловлювань (propositional logic) - Це формальна теорія, основним об'єктом якої є поняття логічного висловлювання. З точки зору виразності, її можна охарактеризувати як класичну логіку нульового порядку. Логіка висловлювань є найпростішою логікою, максимально близькою до людської логіки неформальних міркувань і відома ще з часів античності. Логіка висловлювань, або пропозиційна логіка (18, с. 38-56), є необхідною частиною сучасної логіки, її основою, оскільки має прикладне значення. Логіка висловлювань, як логічна теорія, описує дійсність, стверджуючи чи заперечуючи щось. У природній мові таким висловлюванням відповідають розповідні речення. Логіка висловлювань є двозначною логікою, тобто мова йде про „істинність” чи „хибність”, або, іншими словами, про логічне значення висловлювання. Всі висловлювання у пропозиційній логіці ділять на прості та складні. Структура простих суджень у пропозиційній логіці не аналізується: вони є атомарними і розглядаються лише з боку хибності чи істинності. Мовою логіки висловлювань (далі: ЛВ) називається штучна мова, яка застосовується для аналізу логічної структури складних висловлювань. ПРАВИЛЬНО ПОБУДОВАНІ ФОРМУЛИ – ЦЕ тотожно-істинні і тотожно-хибні
53. Табличний метод перевірки формул логіки висловлень звільняє дослідників від необхідності будувати аксіоматичні системи, в яких теореми обґрунтовуються шляхом виведення їх із системи аксіом. Є ряд формул, які набувають значення «істина» за будь-яких значень істинності змінних, що входять до них. Ці формули називають тотожно істинними формулами, або тавтологіями числення висловлень. Крім того, такі формули є логічними законами. Формули, які набувають значення «ложність» за всіх значень змінних, що входять до них, називають тотожно ложними. Тотожно ложні формули — це суперечності, або, інакше, суперечності — це формули логіки висловлень, які за будь-якого набору значень своїх пропози-ційних змінних набувають значення «ложність». Усі фор- і мули логіки висловлень, що не є суперечностями, вважа- І ють виконуваними. Тотожно істинні й тотожно ложні формули являють і собою постійні б у л є в і функції, які набува ють тільки одного значення, оскільки воно не залежить від змінних, що входять до формули. На відміну від тотожно істинних, виконуваних, тотож-1 но ложні формули невиконувані. Для більш конструктивної характеристики виконува-ності можна сказати: виконуваними формулами є такі, яка хоча б за одного розподілу значень істинності пропозиційних змінних, що входять до них, набувають значення «істина». • Якщо цієї умови не дотримано, говорять, що формули! невиконувані, тобто ложні. Кожна виконувана множина формул несуперечна. Спосіб, за яким щодо будь-якої формули можна визначити, до якого виду формул вона належить, називають розв'язувальною процедурою. Проблема вирішення полягає в тому, щоб відшукати такий спосіб. Для логіки висловлень ним є побудова таблиць істинності, а також перебудова досліджуваної формули в одну з так званих нормальних форм. У зв'язку з посиланнями на табличний метод перевірки логічних формул наводимо більш детальну характеристику логічних сполучників. Логічні сполучники найзручніше характеризувати за допомогою таблиць істинності, де міститься відповідь на запитання про те, коли складне висловлення істинне, а коли ложне. 54. При доведены законів часто в таблиці виділяють окремо останню колонку для виконання еквіваленціїї лівої і правої частини різних законів. Тому якщо виявляється, що еквіваленція цих обох частин має всі значення логічної вартості, що =1, то таку формулу називають логічним законом, а логічне значення вартості називають тотожно-істинним. Якшо ж при побудові формули шляхом встановлення еквіваленції між правою і лівою частинами, в тій колонці дістають різні значення, то формула – виконувана. Якщо ж при цьому всі значення лог. Вартості = 0 то формула тотожна хибна.
55. Натуральне числення логіки висловлювань іноді називають системою натурального виводу (СНВ). Оскільки СНВ базується на дедуктивних умовиводах, вона широко використовується для отримання нових і доведення наявних знань. Натуральним таке виведення висновку називається з огляду на його наближеність до природного міркування. У натуральному численні логіки висловлювань, яке базується на правилах дедуктивного умовиводу.одержуваних
56. Існують аксіоматичне і натуральне числення логіки висловлювань. Натуральне числення має перевагу порівняно з аксіоматичним, істотно спрощуючи пошукові ланцюги за рахунок зміни громіздких доведень значно лаконічнішими виводами. Натуральне числення логіки висловлювань іноді називають системою натурального виводу (СНВ). Оскільки СНВ базується на дедуктивних умовиводах, вона широко використовується для отримання нових і доведення наявних знань. Натуральним таке виведення висновку називається з огляду на його наближеність до природного міркування. У натуральному численні логіки висловлювань, яке базується на правилах дедуктивного умовиводу, істинність одержуваних знань визначається не конкретним змістом засновків, а залежить лише від їхньої істинності й коректності застосування до них правил виводу, що і є можливим завдяки формалізації. Отже, якщо відомі нам вихідні дані, виражені природною мовою, ми перекладемо на мову логіки висловлювань (тобто формалізуємо їх), то матимемо можливість алгоритмізованого виведення істинного висновку, який потім знову перекладається на природну мову та виступає розв'язком задачі. Такий спосіб аналізу вихідних даних набагато скорочує час отримання істинного висновку.
57.Основні логічні характеристики СНВ — несуперечливість і повнота. Несуперечливість означає, що в ній не можна одночасно довести певне судження та його заперечення, тобто не можуть бути одночасно доведені формули А і ІА. Із істинних засновків можна отримати тільки істинні висновки. Отже, якщо в процесі виведення прийняли якесь припущення і дійшли суперечливого висновку, то наш результат свідчить про неправомірність прийнятого припущення. Повнота означає, що кожний логічний закон (тотожно-істинна формула) може бути у цій системі доведеним. У натуральному численні логіки висловлювань, яке базується на правилах дедуктивного умовиводу, істинність одержуваних знань визначається не конкретним змістом засновків, а залежить лише від їхньої істинності й коректності застосування до них правил виводу, що і є можливим завдяки формалізації Гвоздік О.І. Логічні числення: принципи побудови та застосування в юриспруденції. - К., 2003.- С.106.. Отже, якщо відомі нам вихідні дані, виражені природною мовою, ми перекладемо на мову логіки висловлювань (тобто формалізуємо їх), то матимемо можливість алгоритмізованого виведення істинного висновку, який потім знову перекладається на природну мову та виступає розв'язком задачі. Такий спосіб аналізу вихідних даних набагато скорочує час отримання істинного висновку. Основні логічні характеристики СНВ — несуперечливість і повнота. Несуперечливість означає, що в ній не можна одночасно довести певне судження та його заперечення, тобто не можуть бути одночасно доведені формули А і ІА. Із істинних засновків можна отримати тільки істинні висновки. Отже, якщо в процесі виведення прийняли якесь припущення і дійшли суперечливого висновку, то наш результат свідчить про неправомірність прийнятого припущення. Повнота означає, що кожний логічний закон (тотожно-істинна формула) може бути у цій системі доведеним. 58. 59. Логіка предикатів як система створюється відповідно до загальних принципів побудови формальних систем. Особливість логіки предикатів полягає в тому, що вона є складнішою і за семантикою, і за синтаксисом порівняно з логікою висловлювань. Розрізняють семантику та синтаксис логіки предикатів.труктура логіки предикатів (ЛП) - алфавіт, правила побудови формул із символів алфавіту, правила дедуктивного виведення з аксіом нових формул (доведення теорем), правила інтерпретації.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.112.169 (0.011 с.) |
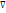 Xєx){хрх} – рефенсивність
Xєx){хрх} – рефенсивність


