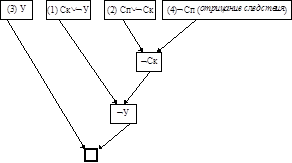Глава 2. Введение в математическую логику

Глава 2. Введение в математическую логику

 

Целью главы является демонстрация некоторых связей между продуктивным мышлением человека, порождающим новое знание, и алгоритмическим функционированием компьютеров. В результате изучения материала этой главы читатель должен освоить:

· общее представление о построении и использовании моделей для решения инженерных проблем;

· формально-логические аспекты формулировки теорем и методов их доказательства;

· методы логического вывода для логики высказываний;

· основы логики первого порядка;

· основы логического вывода в логике предикатов первого порядка;

· формальные основы логического программирования.

 

Содержание главы 2:

2.1 Формальные модели

2.2 Логика высказываний

2.2.1 Формулировка и доказательство теорем

2.2.2 Проверка доказательных рассуждений

Силлогизмы

Логическое следствие

Основная теорема логического вывода

Приведение к нормальным формам

Метод резолюции

Другие методы

Адекватность логики высказываний

2.3 Основы логики предикатов и логического вывода

2.3.1 Предикаты

Свободные и связанные переменные

Интерпретации

Эквивалентности логики предикатов

2.3.2 Логический вывод в логике предикатов

Скулемовская стандартная форма

Алгоритм унификации

2.3.3 Логическое программирование

Логический вывод в Прологе

Применение логического вывода для анализа схем

2.3.4 Экспертные системы

 

Задачи

ЛИТЕРАТУРА

 

Формальные модели

Предмет изучения в этой главе - начала математической, или формальной логики. Математическая логика - это наука, которая занимается анализом суждений и доказательств, используемых человеком для обоснования нового знания, произведенного из установленных фактов. В логике используется специально созданный формализованный язык, подчиняющийся своей системе анализа. Логика исследует схемы рассуждений, которые верны в силу одной их формы, независимо от содержания. Фактически, логика - это множество правил манипулирования формулами, представляющими формы рассуждений. Формальная логика игнорирует смысл, содержание предложений естественного языка, для которых формулы логики являются моделями.

Отвлечение от содержания предложений языка в формальной логике есть результат применения операции абстрагирования к рассуждениям естественного языка. Абстрагирование является основным этапом при построении математической модели, оно широко используется в науке для выборочного исследования некоторых аспектов исследуемой проблемы. Цель абстрагирования - выделение тех аспектов, которые существенны для исследования и решения проблемы и игнорирование тех аспектов, которые несущественны, усложняют проблему, делают анализ менее общим или вообще невозможным.

При научном подходе, на уровне рационального исследования, мы имеем дело не с материальными объектами во всем многообразии их свойств, а с абстракциями от материальных объектов. Реальные объекты и ситуации обычно бесконечно сложны, и абстракция применяется для того, чтобы ограничить эту сложность, дать возможность принимать решения. С помощью абстрагирования человек строит формальные модели самых разнообразных по своей природе понятий, процессов и явлений, сущностей реального мира. Такие формальные модели, будучи построенными, далее допускают анализ и преобразование с помощью формальных же средств: абстракции сами могут быть исследованы с точки зрения их свойств (структура, элемент, отношение, и т.д.), и при таком анализе исследователь может отвлечься от окружающей реальности, оставаясь в рамках построенной им знаковой системы. Формальные модели позволяют выразить некоторые свойства объекта в точных терминах математических определений и аксиом так, что затем можно “вывести” свойства этой модели, которые объяснят известные и предскажут новые свойства исследуемой реальной сущности. Именно на основе научного подхода к решению инженерных проблем получено бессчетное число впечатляющих результатов в технике, в связи с чем давно укоренилась поговорка " Нет ничего более практичного, чем хорошая теория ". Получая в результате анализа моделей какие-либо выводы, исследователь пытается применить эти результаты к той области реального мира, отображением которой является модель, построенная в результате абстракции. Поскольку все абстракции неполны и неточны, можно говорить только о приближенном соответствии с реальностью тех результатов, которые получены исследованием на моделях. Соответствие законов движения, связей и отношений объектов модели соответствующим элементам реального мира называется адекватностью, и степень адекватности определяет, применимы ли такие результаты к конкретной проблеме в реальном мире. Часто адекватность модели определяется рядом условий и ограничений на сущности реального мира, и для того, чтобы использовать результаты анализа, полученные на модели, необходимо тщательно проверять эти ограничения и условия (или обеспечить их выполнение).

 

 

Рис.2.1 Соотношение моделей и реальности

 

В предыдущей главе стояла проблема построения конечных функциональных преобразователей в реальном мире. Эта проблема была решена полностью в соответствии с рис.2.1. Вместо того, чтобы непосредственно начать строить эти преобразователи из реальных объектов (т.е. использовать чисто эмпирический подход, или подход "тыка"), мы представили эту проблему как задачу построения двоичных функций, реализующих требуемое функциональное отображение (т.е. сначала выполнили абстрагирование). Мы затем использовали систематический метод решения этой математической задачи (преобразование модели). На следующем этапе мы также, рассмотрели, как произвольные двоичные функции могут быть реализованы из электронных переключателей и транзисторов (фактически, мы занимались вопросами конкретизации, реализации абстрактной модели). Адекватность реализации модели логических функций обеспечивается в этой конкретной проблеме поддержанием в определенных границах напряжений и токов в электронных переключателях, определенных временных ограничений на работу переключателей и т. д.. Всеми этими средствами достигается коммутативность диаграммы рис.2.1 в решении этих проблем (коммутативность этой диаграммы мы понимаем здесь как возможность получения одного и того же результата из исходных объектов двумя путями: первый - это непосредственным выполнением преобразований объектов в мире вещей, второй - это выполнением операции “ абстрагирование ” и переходом в мир моделей, затем выполнением операции “ преобразование моделей ” и, наконец, выполнением операции “ конкретизация ” с возвращением в мир реальных объектов).

Отметим, что на рис.2.1 ясно видны различия в задачах фундаментальных и инженерных наук:

* Теоретики занимаются внутренними проблемами теорий: разработкой абстрактных моделей, разработкой методов их преобразования и анализа. Они интересуются проблемами, лежащими на рис.2.1 в области «мира идей». В значительно меньшей степени их интересуют вопросы абстрагирования и адекватности моделей, их интерпретация в различных приложениях.

* Перед инженерами стоит задача построения и анализа реальных объектов, но вместо решения ее непосредственно, они сначала абстрагируются от всех деталей реальности, которые несущественны для решения поставленной проблемы, выбирают модель, которая отражает существенные детали, пользуются разработанными теоретиками методами преобразования и анализа моделей, после чего решают исходную задачу с помощью интерпретации и применения этих теоретических результатов в реальном мире. Для инженеров проблема проверки и обеспечения адекватности используемых моделей является определяющей. Важной является также проблема выбора среди множества формальных моделей такой модели, в рамках которой исходная проблема имеет решение. Чаще всего рамки модели накладывают существенные ограничения на применимость результатов этого подхода в реальном мире. На рис.2.1 область их главных интересов – это проблемы связи мира реального и мира идей, т.е. вопросы адекватного использования существующих моделей для решения конкретных задач практики.

Формальная математическая логика решает проблемы проверки правильности рассуждений в естественном языке (реальный мир), строя свои модели и правила их преобразования. Для этого логика вводит свои языки - систему формальных обозначений (формулы) и правила их преобразования. Поэтому логику можно рассматривать как множество правил манипулирования формулами, описывающими утверждения естественного языка. В результате конкретизации (интерпретации) результатов и выводов формальной логики (новых полученных формул) мы получаем новые предложения естественного языка, можем оценить свойства исходных предложений и т.д. Следует ясно понимать, однако, при каких ограничениях выводы, полученные с помощью формализма математической логики, мы можем использовать в реальной жизни.

Логика высказываний

Из всего разнообразия естественного языка логика высказываний имеет дело только с узким кругом утверждений - повествовательных предложений, которым может быть приписано значение “истина” либо “ложь”. Каждому элементарному утверждению в логике высказываний сопоставляется высказывание, обозначающееся буквой. Истинностные значения, которые можно приписать высказываниям, обычно изображаются “И” и “Л”, “1” и”0” или True и False. Кроме простейших высказываний, структура которых не анализируется (они поэтому называются атомами) вводится понятие сложного высказывания или формулы - комбинации более простых высказываний.

Определение 2.1. Формулы логики высказываний определяются рекурсивно над счетным множеством атомов (элементарных высказываний) Á с помощью символов операций (связок) Ø, Þ и скобок “(“ и “)”:

1. Логические константы True, False есть формулы.

2. Любой атом из Á есть формула.

3. Если Р - формула, то Ø(Р) тоже формула.

4. Если Р, Q - формулы, то (PÞQ) - тоже формула.

5. Никаких других формул в логике высказываний нет. ÿ

В логике для сокращения формул используются записи:
(PÚQ) для ((ØP)ÞQ),`

(P&Q) для Ø(Ø(P)Ú(ØQ)),

(PÛQ) для (PÞQ)&(QÞP),

и, кроме того, вводятся правила приоритетов операций для уменьшения скобок в формулах.

Интерпретацией называется придание всем атомам некоторых истинностных значений. Значения формул на всех возможных интерпретациях определяется на основе таблиц истинности для основных символов операций (связок) Ø, Þ:

 

Таблица 2.1 Таблица 2.2

Р	ØP		Р	Q	PÞQ
False	True		False	False	True
True	False		False	True	True
			True	False	False
			True	True	True

Совершенно очевидно, что логика высказываний и теория булевых функций имеют теснейшую связь: обе эти модели являются булевыми алгебрами. Истинностные значения True и False в логике соответствуют 1 и 0, пара основных логических связок - отрицание и импликация - составляют базис (базис Фреге), и все остальные производные логические связки соответствуют известным нам булевым функциям. Двоичные переменные, принимающие значения 1 или 0 в теории булевых функций соответствуют высказываниям, принимающим значения True или False в логике. Для простоты мы дальше будем пользоваться 1 и 0 или t и f как истинностными значениями и всеми известными нам булевыми функциями в виде логических связок, а также результатами и терминологией, известными нам из теории булевых функций. Логические формулы будем называть логическими функциями (они являются функциями, сопоставляющими каждой интерпретации своих аргументов истинностные значения t или f).

Определение 2.2. Литерой будем называть атом или его отрицание. Две литеры будем называть противоположными, если одна из них является отрицанием другой. ÿ

В формальной логике большую роль играют формулы, принимающие одно и то же значение True на всех интерпретациях. Такие формулы называются общезначимыми или тавтологиями. Формула, принимающая значение False на всех интерпретациях своих аргументов, называется невыполнимой. Импликации в естественном языке соответствует связка “ если... то …”.

При всей похожести теорий, задачи, которые они решают, разные. Теория двоичных функций занимается проблемой реализации преобразователей информации. Формальная логика работает с абстракциями, построенными из предложений и рассуждений естественного языка, и интерпретации ее выводов также лежат в области естественного языка.

Пример 2.1 Проанализируем предложение: “ Порядочный человек не может быть вором ”. Предложение состоит из двух более простых утверждений, которые мы представим в модели атомами: П - “ некто есть порядочный человек ”; В - “ некто является вором ”.

Логическая формула, представляющая приведенное выше предложение, очевидно имеет вид: ПÞØВ. Существует несколько формул, эквивалентных данной: ØПÚØВ; Ø(П&В); ВÞØП. Интерпретируя эти формулы в естественном языке, получим следующие утверждения, которые все эквивалентны между собой:

· ПÞØВ: “ Порядочный человек не может быть вором ”

· (ØПÚØВ): “ Или он не порядочный человек, или же он не вор ”;

· Ø(П&В): “ Порядочность и воровство несовместимы ”;

· ВÞØП: “ Если человек вор, то он не является порядочным человеком ”.

Другой пример. Утверждение “ Симпсон будет признан судом виновным тогда и только тогда, когда все 12 присяжных заседателей признают его виновным ” в формульной записи представится так: ВÛ(П₁& П₂& …&П₁₂). Эквивалентная формула: ØВÛØ(П₁& П₂& …&П₁₂) по закону де Моргана может быть преобразована так: ØВÛ(ØП₁ÚØП₂Ú…ÚØП₁₂), что можно интерпретировать как: “ Симпсон не будет признан судом виновным тогда и только тогда, когда хотя бы один из 12 присяжных заседателей не признает его виновным ”. ÿ

С эквивалентностью этих предложений в естественном языке трудно спорить, но на этом пути все же следует быть осторожным. Например, предложения “ Он убил, и ему стало страшно ” и “ Ему стало страшно, и он убил ”, полностью эквивалентные с точки зрения формальной логики, вовсе не эквивалентны в естественном языке. Далее, принятое в формальной логике правило, согласно которому любое высказывание может быть только либо истинным, либо ложным, а третьего не дано, не всегда выполняется в реальной жизни (например, какое истинностное значение приписать предложению “ Это предложение ложно ”, которое не может быть ни истинным, ни ложным). Особые трудности вызывает соотношение формальной импликации и причинно-следственных отношений в естественном мире. Например, фраза: “ Если прошел дождь, то дорога мокрая ” утверждает очевидную связь между фактами А (прошел дождь) и В (дорога мокрая), что выражается логической формулой АÞВ. Из житейского опыта мы связываем с этим причинно-следственным отношением также и дополнительное знание: “ Если дождя не было, то дорога сухая ”, т.е. формула ØАÞØВ тоже справедлива, ее можно считать следствием исходной формулы. Однако две логические формулы АÞВ и ØАÞØВ совершенно различны, из истинности первой формально не следует истинность второй.

Монографии, написанные ведущими специалистами по формальной логике, большое внимание уделяют этой проблеме адекватности - условиям применимости выводов и результатов формальной логики в естественном языке (см., например, [П82]). Результаты формальной логики могут быть применены к высказываниям естественного языка только если выполняются ее постулаты, в частности, высказывания являются только либо истинными, либо ложными (“ черно-белый взгляд на мир ”), они не включают никаких уровней уверенности-неуверенности и возможности, все причинно-следственные отношения между фактами явно выражены, истинностные значения высказываний статичны, не меняются во времени и т.д. Представляемая здесь ветвь логики формализует лишь самую простую часть тех закономерностей, которым подчиняется мышление и язык. Однако, даже эта часть является удивительной и впечатляющей по своим результатам. Существуют различные интересные расширения классической логики, например, многозначная логика, формализующая конкретный набор степеней уверенности в истинности высказываний, нечеткая логика, в которой можно оперировать с оценками степени уверенности (вероятностями) в истинности высказываний, темпоральная логика, позволяющая формулировать высказываниями о свойствах систем, проходящих изменяющиеся последовательные стадии, и т.д. Эти логики, однако, выходят за рамки нашего рассмотрения.

Метод резолюции

Этот метод использует тот факт, что если некоторая формула является невыполнимой, то наиболее сильное следствие этой формулы - константа False. Предложенный в 1965г. Дж. Робинсоном [R65] метод резолюции позволяет получить максимально сильное следствие множества формул с помощью систематической процедуры последовательного построения логических следствий формулы, называемых резольвентами. Иными словами, метод резолюции обладает свойством полноты: для формулы Ф следствие False обязательно будет получено, если Ф - невыполнима.

Теорема 2.4. Пусть В - логическое следствие формулы А. Тогда А&В º А.

Доказательство теоремы легко проводится на основании определения понятия логического следствия. Действительно, пусть условие теоремы выполнено. Тогда в соответствии с теоремой 2.1, АÞВ º True. Отсюда АºА& True ºА&(АÞВ) ºА(ØАÚВ) ºА&ØАÚА&Вº False ÚА&ВºА&В. ÿ

Определение 2.5. Резольвентой двух дизъюнктов D1ÚL и D2ÚØL называется дизъюнкт D1ÚD2. ÿ

Теорема 2.5. Резольвента является логическим следствием порождающих ее дизъюнктов.

Доказательство. Пусть D1ÚL и D2ÚØL - два дизъюнкта. Тогда D1ÚD2 - их резольвента. Легко показать, что формула (D1ÚL)&(D2ÚØL)Þ(D1ÚD2) общезначима. По теореме 2.1 отсюда следует заключение теоремы. ÿ

Метод резолюции доказательства невыполнимости формулы Ф=F₁F₂...F_kØR состоит в том, что формула Ф представляется в КНФ, и к ней конъюнктивно присоединяются все возможные резольвенты ее дизъюнктов и получаемых в процессе доказательства резольвент. Полнота метода резолюции состоит в том, что он гарантирует получение для формулы Ф следствия False, если Ф - невыполнима. Если же, перебрав все возможные резольвенты формулы Ф, мы не нашли пустую резольвенту, то Ф не является невыполнимой.

Пример 2.8. Доказательство правильности рассуждения “ Узнала - спросила ” сводится к проверке невыполнимости формулы Ф=F1&F2&F3&ØR, где F1=ØСкÞØУ, F2=ØСпÞØСк, F3=У и R= Сп.

Перечислим все дизъюнкты конъюнктивной нормальной формы Ф и построим возможные резольвенты:

N	Дизъюнкт	Откуда он получен	Интерпретация
(1)	СкÚØУ	- первое утверждение:	Известно, что: “Если бы он не сказал ей, она бы не узнала”;
(2)	СпÚØСк	- второе утверждение:	и что “Если бы она его не спросила, он бы не сказал ей”;
(3)	У	- третье утверждение:	и что “Она узнала”.
(4)	ØСп	- отрицание следствия:	Докажем, что "Она спросила”. Предположим противное,т.е. что "Онане спросила”.
(5)	ØСк	- резольвента 2 и 4;	Отсюда следует (поскольку по (2): “Если бы она его не спросила, он бы не сказал ей”)что "Он не сказал ей ".
(6)	ØУ	- резольвента 1 и 5;	Отсюда следует (поскольку по (1):“Если бы он не сказал ей, она бы не узнала”)что "Она не узнала ".
(7)	ÿ	- резольвента 3 и 6, пустой дизъюнкт	Мы пришли к противоречию: ведь известно же (3), что“Она узнала”. Следовательно, нашепредположениеневерно (оно противоречит фактам), т.е. "Онане спросила”.

Доказательство методом резолюции сделаем более наглядным, представив его графически:

 

Рис.2.2. Графическое представление доказательства методом резолюции

 

Доказательство методом резолюции очень близко обычному словесному доказательству от противного. Это демонстрирует интерпретация последовательных формул вышеприведенной таблицы. Проинтерпретируем еще раз это доказательство в естественном языке по графу рис.2.2.

Рассуждение: “Если бы он не сказал ей, она бы и не узнала. А не спроси она его, он и не сказал бы ей. Но она узнала. Следовательно, она спросила.”

Доказательство (см. рис.2.2): “ Предположим противное, т.е. что она не спросила. Тогда из второго утверждения следует, что он ей не сказал. Отсюда, и из первого утверждения следует, что она не узнала. Но в третьем утверждении говорится, что она узнала. Таким образом, предположив, что следствие неверно, мы пришли к противоречию. Поэтому следствие верно. ”

Для рассуждения примера 2.2: “В хоккей играют настоящие мужчины. Трус не играет в хоккей. Я в хоккей не играю. Значит, я трус(?!)” метод резолюции дает (см таб.2.5):

 

(1) ØХÚМ - первое утверждение: “В хоккей играют настоящие мужчины”;

(2) МÚØХ - второе утверждение: “Трус не играет в хоккей”;

(3) ØХ - третье утверждение: “Я в хоккей не играю”;

(4) М - отрицание следствия: “ Предположим, что неверно, что "Я трус" ”;

Резольвент нет

Мы не можем построить здесь ни одной резольвенты, не говоря уж о пустой. Отсюда можно заключить, что вывод в этом рассуждении не является логическим следствием высказанных утверждений и не следует формально из их истинности. Для доказательства (или опровержения) этого вывода необходимы дополнительные факты.

Определение 2.6. Пусть S - множество дизъюнктов. Резолютивный вывод С из S есть такая конечная последовательность С₁,...,С_k дизъюнктов, что С_k = C и каждый дизъюнкт С_i или принадлежит S или является резольвентой дизъюнктов, предшествующих С_i. Вывод пустого дизъюнкта из S называется опровержением S. ÿ

Следующая теорема является важнейшей теоремой теории логического вывода в логике высказываний: она утверждает, что используя единственное правило вывода - резолюцию, мы можем проверить правильность любого заключения из фактов, последовательно получая резольвенты и присоединяя их к исходной формулировке.

Теорема 2.6 (о полноте метода резолюции). Множество дизъюнктов S невыполнимо тогда и только тогда, когда существует резолютивный вывод пустого дизъюнкта из S.

Необходимость. Доказательство того, что при невыполнимости S всегда найдется резолютивный вывод пустого дизъюнкта из S за конечное число шагов, здесь опускается.

Достаточность. Пусть из S существует резолютивный вывод пустого дизъюнкта. Докажем, что S невыполнимо. Поскольку резольвента  есть логическое следствие порождающих ее дизъюнктов D_i и D_k, то конъюнктивное присоединение резольвенты  к формуле S не меняет ее значения, поскольку S=AD_iD_k, а D_iD_kºD_iD_k согласно теоремам 2.4 и 2.5. Если среди резольвент Ф существует пустая резольвента, соответствующая ее логическому следствию False, то Ф невыполнима, поскольку эквивалентна формуле с конъюнктивным членом False. ÿ

Перебор всех возможных резольвент можно организовать по-разному, и разные стратегии построения резольвент будут (в среднем) иметь различную эффективность (число шагов вывода до получения положительного или отрицательного ответа). Одной из наиболее эффективных стратегий является стратегия движения “ от цели ” - получение на каждом шаге резольвент из двух дизъюнктов, один из которых - это цель доказательства (инверсия предполагаемого следствия) или резольвента-потомок этой цели. Эта стратегия особенно эффективна в языках логического программирования, где только небольшое число фактов общей базы данных действительно имеют отношение к заданному вопросу. Мы рассмотрим использование метода резолюции в языках логического программирования ниже.

Другие методы. Использование семантических деревьев для проверки общезначимости или невыполнимости формулы было предложено Куайном. Идея основывается на том, что часто нет необходимости строить все дерево до листьев: в некотором узле значение функции может быть определено сразу для всех листьев, которые могут быть построены из этого узла. Метод Куайна был усовершенствован Девисом и Патнемом, предложившими для проверки невыполнимости формулы предварительно представить эту формулу в КНФ. Функция представляется в виде совокупности дизъюнктов, каждый из которых - просто множество литер, и алгоритм сводится просто к вычеркиванию литер из этих множеств в узлах семантического дерева.

Адекватность логики высказываний. Вопрос об адекватности математической модели при решении конкретных проблем в реальной жизни, как уже говорилось выше, лежит вне самого математического аппарата, это проблема, которую должен решать человек, использующий этот аппарат для решения задач практики. В области формализации рассуждений естественного языка всегда надо быть осторожным, применяя выводы логики высказываний к реальной жизни. Хорошую иллюстрацию этому дает так называемая “задача Кислера”, приведенная в монографии С. Клини “Математическая логика”. Рассмотрим ее в несколько измененной постановке.

Браун, Джонс и Смит обвиняются в преступлении. На допросе они под присягой дали показания:

Браун: Джонс виновен, а Смит невиновен (Д&С).

Джонс: Браун без помощи Смита это не смог бы сделать (БÞC).

Смит: Я невиновен, но кто-то из них виновен (ØC&(БÚД)).

Из этих утверждений следует, что виноват Джонс, а двое других подозреваемых невиновны (докажите!). Но задумаемся, действительно ли мы можем считать эти посылки истинными? Что, если виновный лжет, а невиновный говорит правду? В этом случае нахождение максимально сильного следствия шести посылок:

F1:ØБÞ(Д&С); F3:ØДÞ(БÞC); F5:ØСÞØC&(БÚД);

F2: БÞØ(Д&С); F4: ДÞØ(БÞC); F6: СÞØ(ØC&(БÚД));

приводит к полностью противоположному выводу. Если же мы будем полагаться на информацию только тех, кто невиновен (т.е учитывать только утверждения F1, F3, F5), то мы получим третий результат: установить в точности, кто виновен, без дополнительной информации нельзя. Таким образом, результаты анализа одной и той же ситуации с привлечением одного и того же аппарата - логики высказываний - существенно меняются в зависимости от того, как мы формализуем задачу проверки правильности рассуждений, какие факты мы будем считать установленными.

Другим примером, иллюстрирующим это положение, является доказательство древнегреческого философа Зенона того, что движения нет: “ Если тело движется, то движение может происходить либо там, где тело есть, либо там, где тела нет. Но движение не может происходить там, где тело есть, потому что тогда бы оно стояло на месте. Движение не может также происходить там, где тела нет: если там тела нет, то как оно может там двигаться?. Следовательно, тело двигаться не может ”. Логическая структура этого доказательства совершенно правильна, но формальная логика не может отвечать за то, что содержание умозаключения неверно. Движение все же есть!

Предикаты

Логика высказываний оперирует с атомами. Атомы являются абстракциями простейших повествовательных предложений, которые могут быть истинными или ложными. Атом рассматривается как неделимое целое, его структура не анализируется. Таким образом, аппарат, подходы и результаты логики высказываний могут быть применены только к очень узкому классу ситуаций - самых простых рассуждений на естественном языке.

В естественном языке встречаются и более сложные повествовательные предложения, истинность которых может меняться при изменении объектов, о которых идет речь, хотя структура предложений не меняется. Например, предложение “Джон любит Мэри” может быть истинным, а предложение “Джон любит Мэгги” ложным. В логике такие предложения, истинность которых зависит от параметров, абстрагируют с помощью предикатов. Например, предикат Любит(х,у) на паре <Джон, Мэри> может принимать значение истина, а на паре <Джон, Мэгги> - ложь. На латыни слово “ предикат ” (praedicatum) означает “ сказуемое ”, т.е. то, что в элементарном суждении утверждается о субъекте этого суждения, т.е. свойства этого оюъекта. Например, высказывание “ Собака имеет хвост” истинно, “ Лошадь имеет хвост” истинно, а “ Человек имеет хвост” ложно. Поэтому заменив субъект в суждении переменной x, получим некую форму “ х имеет хвост”, которая является функцией от х и принимает значения истинно для одних субъектах-аргументах этой функции и ложно для других. Формализация подобной высказывательной формы и называется предикатом, т.е. функцией, принимающей истинностные значения (истина либо ложь) и определенной на произвольной области изменения своей переменной; n-местный предикат является естественным обобщением функции одной переменной.

Определение 2.7. n-местным предикатом Р(х₁,...,х_n) называется функция Р: М ⁿ®{ True, False }, определенная на наборах длины n элементов некоторого множества М и принимающая значения в области истинностных значений (рис.2.3, а). ÿ

Множество М называется предметной областью предиката, а х₁,...,х_n - предметными переменными. Пусть М - множество натуральных чисел и n = 2. Двуместный предикат Р(х,у): х³у+3 истинен на парах <25,1> и <15,12> и ложен на паре <1,1>. Поскольку предикат каждому элементу множества М ⁿ ставит в соответствие True или False, то можно считать, что предикат выделяет на М ⁿ некоторое подмножество, на котором он истинен (рис.2.3, б). Таким образом, предикат на М может характеризовать (задавать) некоторое подмножество элементов М, а именно тех, на которых он истинен.

Предикаты могут быть связаны логическими связками, например, Р(х,у) ÚØQ(х,у). Рассмотрим формулу РÞQ. Она принимает истинное значение на тех аргументах, на которых предикат Р ложен или же предикат Q истинен. Очевидно также, что если на каждом элементе множества М ⁿ, на котором предикат Р истинен, предикат Q тоже истинен, формула РÞQ общезначима. Таким образом, формула РÞQ общезначима тогда и только тогда, когда множество истинности предиката Р является подмножеством множества истинности предиката Q, или, что то же, предикат P сильнее предиката Q, как это показано на рис.2.3, в).

Рис.2.3. Графическое представление предикатов

 

В качестве аргументов предикатов можно использовать и функции, принимающие значения из предметной области. Например, функция Отец(х) пусть абстрагирует предложение естественного языка “ Отец человека по имени х ”. Тогда Любит(Отец(Отец(х)),у) - тоже предикат, он будет принимать истинное значение на паре <Мэри, Джон>, если дедушка Мэри действительно любит Джона.

Итак, в отличие от логики высказываний, в которой структура простейших утверждений не анализируется (они там называются атомами), в логике предикатов атомный предикат имеет структуру.

Определение 2.8. Термом будем называть переменную или константу предметной области М, или функцию, принимающую значения в предметной области. Атомный предикат - это n-местная функция F(t₁,...,t_n), принимающая значение в множестве { True, False }, где t_i - термы. ÿ

Введем понятие формулы - комбинации простейших утверждений.

Определение 2.9. Правильно построенные формулы (ППФ) логики предикатов - это комбинация атомных предикатов и констант с логическими связками. Они определяются рекурсивно над множеством атомных предикатов с помощью символов операций (связок) Ø, Þ, скобок и одной дополнительной связки ", которая читается “ для всех ”. Рекурсивно ППФ определяются так:

1. Логические константы True, False есть формулы.

2. Атомный предикат есть формула.

3. Если Р - формула, то Ø(Р) тоже формула.

4. Если Р, Q - формулы, то (PÞQ) - тоже формула.

5. Если Р - формула, то ("х)Р тоже формула.

6. Никаких других формул в логике предикатов нет.

Фактически, добавлением в логике предикатов по сравнению с логикой высказываний является то, что предикаты обычно не имеют фиксированного истинностного значения, их истинность различна для разных значениях их аргументов. В качестве единственной новой логической связки в логике предикатов используется связка ".

В логике предикатов для сокращения формул используются записи:

PÚQ для (ØP)ÞQ,

P&Q для Ø(Ø(P)Ú(ØQ)),

PÛQ для (PÞQ)&(QÞP),

($х)Р для Ø(("х)ØP). ÿ

Новые логические связки " - “ для всех ” и $ - “ существует ” называются кванторами: " - “квантор всеобщности” и $ - “квантор существования”. Формула ("х)Р(х) читается так: “Для всех х выполняется Р(х)”. Очевидно, что это уже не предикат, это константа True либо False, в зависимости от того, действительно ли для каждого элемента х предметной области высказывание Р(х) истинно. Аналогично, логической константой является ($х)Р(х), что читается так: “Существует такое х, что для него выполняется Р(х)”. Для конечной предметной области значения этих связок очевидны. Пусть на М ={x₁,x₂,...,x_n} определен произвольный предикат Р(х). Тогда очевидно:

("х)Р(х) = Р(х₁)&Р(х₂)&...&Р(х_n)=&_{хÎ М} Р(х);

($х)Р(х) = Р(х₁)ÚР(х₂)Ú...ÚР(х_n) =Ú_{хÎ М} Р(х).

Пример 2.9. Пусть Р(х) - предикат, определенный на множестве всех людей и означающий “ х является студентом”. Тогда ("х) Р(х) ложно, а ($х) Р(х) истинно. Формула ("х) Любит(х, Отец(Отец(Джон))) истинна, если все любят дедушку Джона, а формула ($х) [Р(х) ÞØ Любит(Отец(Джон), х)] истинна, если отец Джона не любит хотя бы одного студента. Далее, если R(x,y) - предикат, определенный на множестве всех семейных людей и означающий “х и у - супруги”, то ("х)($y)R(х,y) ¹ ($y)("х)R(х,y). Первая формула истинна, вторая - ложна. ÿ

Свободные и связанные переменные. Область действия переменной, указанной в кванторе, если она не очевидна, определяется скобками, например:

G(x,z) = ("t)[Р(t,z)Ú("u)($y)Q(t,y,u)]Þ("r)R(x,r).

Переменная связана, если она находится в области действия квантора. Связанные переменные можно заменят