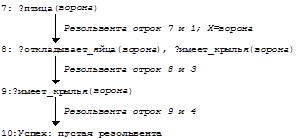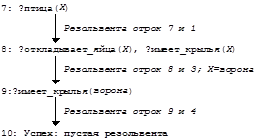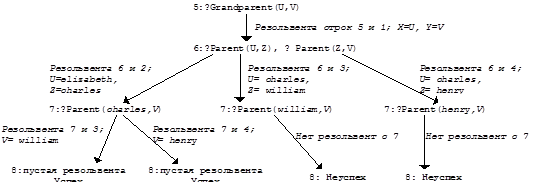Скулемовская стандартная форма

В логическом выводе используют предикаты в предваренной форме, когда все кванторы вынесены в формуле влево, т.е. предваряют формулу. Эту формулу, которая уже не содержит кванторов, можно свести к конъюнктивной нормальной форме. Преобразование в предваренную форму легко выполнить применением свойств эквивалентности и заменой переменных. Например, приведем формулу ("х)P(х)Þ($х)R(x) в предваренную форму:

("х)P(х)Þ($х)R(x) º Ø("х)P(х)Ú ($х)R(x) º ($х) ØP(х)Ú($х)R(x) º ($х)[ØP(х)ÚR(x)] º ($х)[P(х) ÞR(x)].

Логический вывод легко применяется в случае, если в предваренной форме представления фактов присутствует только квантор всеобщности. В логике предикатов разработан метод, позволяющие исключить квантор существования из формулы в предваренной форме. Этот метод связан с введением так называемых “ скулемовских функций ”. Рассмотрим этот метод, опуская обоснования, которые можно найти в [ЧЛ83].

Пусть предикат F находится в предваренной форме (Q₁x₁)…(Q_nx_n)M, где М есть предикат в конъюнктивной нормальной форме, а (Q₁x₁)…(Q_nx_n) - префикс кванторов. Пусть Q_r есть самый левый квантор существования, 1£r£n. Если никакой квантор всеобщности не стоит левее Q_r, то выберем новую константу с, отличную от других констант, входящих в М, заменим все вхождения x_r, встречающиеся в М, на с и вычеркнем (Q_rx_r) из префикса. Если же Q_s1…Q_sm - все кванторы всеобщности, встречающиеся левее Q_r, 1£s₁<s₂<…<s_m<r£n, выбираем новый m-местный функциональный символ f, отличный от всех других функциональных символов, заменим все, заменим все вхождения x_r, встречающиеся в М, на f(x_s1,x_s2,…x_sm) и вычеркнем (Q_rx_r) из префикса. Эту операцию применим для всех кванторов существования в префиксе слева направо; последняя из полученных формул есть скулемовская стандартная форма, к которой, собственно, и применяется алгоритм логического вывода. Константы и функции, использованные для замены переменных квантора существования, называются скулемовскими константами и функциями.

Пример 2.15. Построим скулемовскую стандартную форму предиката ($x)("y)("z)($u)("v)($w) P(x,y,z,u,v,w).

Левее ($x) в формуле нет никаких кванторов всеобщности, левее ($u) стоят кванторы всеобщности ("y) и ("z), левее ($w) стоят кванторы всеобщности ("y), ("z) и ("v). Заменяем переменную х на константу а, переменную u на двухместную функцию f(y,z), а переменную w - на трехместную функцию g(y,z,v). Скулемовская стандартная форма представленной выше формулы - ("y)("z)("v)P(а,y,z,f(y,z),v,g(y,z,v)). ÿ

Пример 2.16. Рассмотрим следующую теорему теории групп [ЧЛ83]. Теорема (о коммутативной группе). Если произведение любого элемента группы G на себя есть единица этой группы, то группа G - коммутативна.

Очевидно, что для доказательства эта теорема должна быть записана формально. Пусть предикат Р(х,у,z) означает следующее утверждение: Если хÎG и уÎG, то zÎG и ху=z (мы опускаем здесь знак бинарной операции умножения группы). Тогда теорема будет выглядеть так (единицу группы обозначим е): ("x) Р(х,х,е) Þ ("u) ("v) ("w)[Р(u,v,w) Þ Р(v,u,w)].

Доказательство теорем обычно проводится на основе аксиом и других теорем, выведенных из этих аксиом. Аксиомами, определяющими любую группу G, являются следующие четыре:

А1: в группе существует единичный элемент (т.е. для любого хÎG хе=х и ех=х)

A2: для каждого элемента группы существует обратный элемент (если х^-1 - обратный к х, то х х^-1= х^-1 х = е).

А3: любая группа удовлетворяет свойству ассоциативности (т.е. х, у и zÎG влечет x(yz) = (xy)z);

 

Формальное выражение этих аксиом:

А1: ("x)[P(е,х,x)&P(х,е,x)];

A2: ("у)($х)[P(x,y,e)&P(y,x,e)].

A3: ("x)("у)("z)("u) ("v)("w) [P(x,y,u) &P(y,z,v) Þ[P(x,v,w)ÛP(u,z,w)] ];

Для доказательства сформулированной выше теоремы В = {("x) Р(х,х,е) Þ ("u) ("v) ("w)[Р(u,v,w) Þ Р(v,u,w)]} просто покажем, что она является логическим следствием аксиом А1-А3. Отрицание этой теоремы:

ØB = {("x) Р(х,х,е) & Ø("u) ("v) ("w) [Р(u,v,w) Þ Р(v,u,w)]} =

{("x) Р(х,х,е) & ($u) ($v) ($w) Ø[Р(u,v,w) Þ Р(v,u,w)]}

Скулемовские формы для аксиом и отрицания следствия:

А1: ("x)[P(e,x,x)&P(x,e,x)];

A2: ("у)[P(i(у),у,e)&P(у,i(у),e)];

A3: ("x)("у)("z)("u) ("v)("w) [P(x,y,u) &P(y,z,v) Þ[P(x,v,w)ÛP(u,z,w)] ];

ØB: ("x){Р(х,х,е) & Ø[Р(a,b,c) Þ Р(b,a,c)]}.

Список дизъюнктов для метода резолюции:

(1) P(e,x,x) из А1;

(2) P(x,e,x) из А1;

(3) P(i(у),у,e) из А2;

(4) P(у,i(у),e) из А2;

(5) Р(х,х,е) из ØВ;

(6) ØP(x,y,u) Ú ØP(y,z,v) Ú ØP(x,v,w) Ú P(u,z,w) из А3;

(7) ØP(x,y,u) Ú ØP(y,z,v) Ú Ø P(u,z,w) ÚP(x,v,w) из А3;

(8) Р(a,b,c) из ØВ;

(9) ØР(b,a,c) из ØВ.

ÿ

Алгоритм унификации

В процедуре доказательства методом резолюций для отождествления противоположных пар предикатов (именно предикаты выступают здесь в роли литер, если говорить в терминах метода резолюции для высказываний) используется так называемая “ процедура унификации ” - приведение аргументов дизъюнктов, для которых ищется резольвента, к унифицированному (одинаковому) виду. В примере 2.14 при поиске резольвенты двух дизъюнктов ØЧеловек(х)ÚСмертен(х) и Человек(Сократ) вместо переменной х можно подставить конкретное значение “ Сократ ” именно потому, что квантор всеобщности предваряет первый дизъюнкт: поскольку это высказывание истинно для любого элемента предметной области (множества людей), то оно справедливо и для конкретного человека по имени Сократ.

Рассмотрим алгоритм унификации конечного множества выражений (см. [ЧЛ83]). Алгоритм унификации пытается найти такие наиболее общие замены переменных в выражениях, чтобы эти выражения стали тождественны. Например, чтобы два выражения Р(х) и Р(а) стали тождественны, необходимо просто переменную х заменить на константу а. Обобщим этот примитивный случай: построим алгоритм, который находит минимальную подстановку переменных всегда, когда она есть. Формализуем простейший случай. Чтобы отождествить Р(а) и Р(х) сначала найдем рассогласование выражений, которое равно {а, х}, а потом попытаемся его исключить конкретизацией переменных. В общем случае рассогласование множества выражений W строится выявлением первой слева позиции, на которой не для всех выражений из W стоит один и тот же символ. Далее с этой позиции из каждого выражения в W выделяются подвыражения, совокупность которых и составляет множество рассогласований. Например, если W есть {P(x, f(y, z)), P(x, a), P(x, g(h(x)))}, то первая позиция рассогласования есть пятая, поскольку у всех выражений четыре первые символа “Р(х,” совпадают. Начинающиеся с пятой позиции подвыражения подчеркнуты; они и составляют множество рассогласований: {f(y, z), a, g(h(x))}.

Алгоритм унификации

Шаг 1. Полагаем k =0, W_k=W, s_k=e.

Шаг 2. Если W_k - содержит только один дизъюнкт, то останов, W - унифицируемо и s_k -наиболее общий унификатор для W. Если нет, найдем D_k - множество рассогласований для W_k.

Шаг 3. Если в D_k существует пара выражений v_k и t_k, такие, что v_k - переменная, а t_k - терм (возможно, другая переменная), не содержащий эту переменную, то положить s_k+1 = s_k·{ t_k / v_k }, W_k+1 = W_k{ t_k / v_k }, k = k +1 и перейти к шагу 2.

В противном случае останов: множество W не унифицируемо.

В этом алгоритме используются обозначения W_k{ t_k / v_k }, что означает подстановку терма t_k вместо всех вхождений переменной v_k, и s_k·{ t_k / v_k }, что означает произведение подстановок с очевидным смыслом. Рассмотрим работу алгоритма на примерах.

Пример 2.17 (а). Наиболее общий унификатор для W={P(x, f(х)), P(z, f(z)}, очевидно, {x/z} (или, {z/x}). После замены переменных W₁={P(x, f(х)), P(х, f(х)}={P(x, f(х))}, содержит только один член - единичный дизъюнкт. Таким образом, замена переменных при резолюции является частным случаем унификации. ÿ

Пример 2.17(б). Найдем наиболее общий унификатор для W={P(a, x, f(g(y))), P(z, f(z), f(u))}.

1. Шаг 1. k =0, W₀=W, s₀=e. Переходим к шагу 2.

2. Шаг 2. W₀ не является единичным дизъюнктом. D₀ = {a, z}. Переходим к шагу 3.

3. Шаг 3. Множество рассогласований D₀ содержит пару (a, z), в которой z- переменная, а терм “а” эту переменную не содержит. Полагаем s₁ =s₀·{а/z}=e·{а/z}={а/z}. W₁=W₀·{а/z} = {P(a, x, f(g(y))), P(a, f(а), f(u))}, k =1.

4. Шаг 2. W₁ не является единичным дизъюнктом. D₁ = {х, f(а)}. Переходим к шагу 3.

5. Шаг 3. Множество рассогласований D₁ содержит пару (х, f(а)), в которой х - переменная, а терм “f(а)” эту переменную не содержит. Полагаем s₂ = s₁·{f(а)/х} = {а/z}·{f(а)/х} = {а/z, f(а)/х}. W₂ = W₁{f(а)/х} = {P(a, f(а), f(g(y))), P(a, f(а), f(u))}, k =2.

6. Шаг 2. W₂ не является единичным дизъюнктом. D₂ = {g(y), u}. Переходим к шагу 3.

7. Шаг 3. Множество рассогласований D₂ содержит пару (g(y), u), в которой u- переменная, а терм “g(y)” эту переменную не содержит. Полагаем s₃ = s₂{g(y)/u} = {а/z, f(а)/х}{g(y)/u} = {а/z, f(а)/х, g(y)/u}. W₃ = W₂{g(y)/u} = {P(a, f(а), f(g(y))), P(a, f(а), f(g(y)))} = {P(a, f(а), f(g(y)))}, k =3.

8. Шаг 2. W₃ содержит только единичный дизъюнкт. Алгоритм завершился. Наиболее общий унификатор для W = {P(a, x, f(g(y))), P(z, f(z), f(u))} - это подстановка s₃ = {а/z, f(а)/х, g(y)/u}, т.е. нужно везде подставить вместо z константу а, вместо х - функцию f(а), а вместо u - функцию g(y). ÿ

Пример 2.18. Докажем справедливость следующего рассуждения [ЧЛ83].

Посылки:

F1:: Некоторые пациенты любят докторов.

F2:: Ни один пациент не любит знахарей.

Заключение:

R:: Никакой доктор не является знахарем.

Выделим элементарные высказывания:

Р(х): “х- пациент”;

D(х): “х- доктор”;

Z(х): “х- знахарь ”;

L(x,y): “x любит у”.

Предикатная запись рассуждения:

F1:: ($x: P(x))("y: D(y)) L(x,y), Некоторые пациенты любят ( всех ) докторов.

F2:: ("x: P(x))("y: Z(y))ØL(x,y), Ни один пациент не любит ( всех ) знахарей.

Это же можно записать и так: F2:: Ø ($x: P(x))($y: Z(y))L(x,y),

R:: ("x: D(x))ØZ(x); Никакой доктор не является знахарем.

Это же можно записать и так: R:: Ø ($x: D(x)) Q(x);

Раскрытие ограниченных предикатов:

F1:: ($x)[P(x)&("y)(D(y)ÞL(x,y))],

F2:: ("x)[P(x) Þ("y)(Z(y) ÞØL(x,y))],

R:: ("x)(D(x)ÞØZ(x));

Отрицание заключения:

ØR:: ($x)Ø(ØD(x)ÚØZ(x)).

Представление посылок и отрицания заключения в предваренной конъюнктивной нормальной форме:

F1:: ($x)("y)[P(x)&(ØD(y)ÚL(x,y))],

F2:: ("x)("y)(ØP(x)ÚØZ(y)ÚØL(x,y)),

ØR:: ($x)D(x)&Z(x).

Представление посылок и отрицания заключения в скулемовской нормальной форме:

F1:: ("y)(P(а)&(ØD(y)ÚL(а,y)),

F2:: ("x)("у)(ØP(x)ÚØZ(у)ÚØL(x,у)),

ØR:: D(b)&Z(b).

Замена переменных:

F1:: ("y)(P(а)&(ØD(y)ÚL(а,y)),

F2:: ("x)("z)(ØP(x)ÚØZ(z)ÚØL(x,z)),

ØR:: D(b)&Z(b).

Здесь произведена замена переменных, связанных квантором всеобщности: в F2 переменная у заменена на z с тем, чтобы не было коллизий с утверждением F1. Алгоритм унификации позволит автоматически произвести необходимую замену переменных при поиске резольвенты. Если этого не сделать, то могут возникнуть коллизии: как, например, унифицировать два предиката Р(х, f(z)) и Р(z, f(x)) из различных дизъюнктов?

Дизъюнкты для доказательства методом резолюции:

(1) Р(а)

(2) ØD(y)ÚL(а,y)

(3) ØP(x)ÚØZ(z)ÚØL(x,z)

(4) D(b)

(5) Z(b)).

Резольвенты:

(6) L(а,b) резольвента (4) и (2)

(7) ØP(а)ÚØZ(b) резольвента (6) и (3)

(8) ØQ(b) резольвента (7) и (1)

(9) ð резольвента (8) и (5) - пустая

Восстановим словесную форму доказательства.

Посылки:

F1:: Некоторые пациенты любят докторов.

F2:: Ни один пациент не любит знахарей.

Заключение:

R:: Следовательно, никакой доктор не является знахарем.

Доказательство.

Предположим противное, т.е. что существует некий доктор, одновременно являющийся и знахарем. Пусть этот человек b (Отрицание следствия, D(b)&Z(b)). Тогда из утверждения (F1:: Некоторые пациенты любят (всех) докторов)следует, что существует пациент (назовем его а), который любит всех докторов, и, конечно, любит конкретного доктора b (L(а,b)). Отсюда и из второго утверждения (F2:: Ни один пациент не любит знахарей) следует, что или а не пациент, или b не доктор (ØP(а)ÚØZ(b)). Но из утверждения F1 мы знаем, что а - пациент, а из отрицания заключения(ØR) по предположению, b -доктор. Таким образом, мы пришли к противоречию, и, следовательно, заключение нашего рассуждения верно. ÿ

Пример 2.16 (продолжение). Докажем теперь теорему о коммутативной группе формально. Для этого нужно просто показать существование пустой резольвенты для множества дизъюнктов Д1-Д9 примера 2.16.

Отметим еще раз, что при нахождении резольвенты двух дизъюнктов, включающих переменные, связанные кванторами всеобщности, эти переменные в разных дизъюнктах не должны совпадать: в каждом дизъюнкте они связаны квантором всеобщности, и "не видны" извне. Поэтому все переменные одного дизъюнкта при применении метода резолюции нужно переименовать так, чтобы они отличались от переменных других дизъюнктов. Эта операция переименования называется разделением переменных. Для данного примера запишем список дизъюнктов после разделения переменных:

Д1: P(e,x1,x1);

Д2: P(x2,e,x2);

Д3: P(i(у1),у1,e);

Д4: P(у2,i(у2),e);

Д5: Р(х3,х3,е);

Д6: ØP(x4,y4,u4) Ú ØP(y4,z4,v4) Ú ØP(x4,v4,w4) Ú P(u4,z4,w4);

Д7: ØP(x5,y5,u5) Ú ØP(y5,z5,v5) Ú Ø P(u5,z5,w5) ÚP(x5,v5,w5);

Д8: Р(a,b,c);

Д9:ØР(b,a,c).

Резольвенты и порождающие их дизъюнкты, построенные при доказательстве теоремы, представлены таблицей:

 

Родители	Унификатор	Полученная резольвента
Д5 и Д7.1	{х3/х5, x3/y5, e/u5}	Д10: ØP(x6,z6,v6) Ú ØP(e,z6,w6) Ú P(x6,v6,w6);
Д8 и Д10.1	{a/х6, b/z6, c/v6}	Д11: ØP(e,b,w7) Ú P(a,c,w7);
Д11.1 и Д1	{b/w7}	Д12: P(a,c,b);
Д9 и Д7.4	{b/x5, a/v5,c/w5}	Д13: ØP(b,y8,u8) Ú ØP(y8,z8,a) Ú ØP(u8,z8,c);
Д5 и Д13.1	{b/x3, b/y8, e/u8}	Д14: ØP(b,z9,a) Ú ØP(e,z9,c);
Д14.2 и Д1	{c/z9}	Д15: ØP(b,c,a);
Д15 и Д6.4	{b/u4, c/z4, a/w4}	Д16: ØP(x10,y10,b) Ú ØP(y10,c,v10) Ú ØP(x10,v10,a);
Д12 и Д16.1	{a/x10, c/y10}	Д17: ØP(c,c,v11) Ú ØP(a,v11,a);
Д5 и Д17.1	{c/x3, e/v11}	Д18: ØP(a,e,a);
Д18 и Д2	{a/x2}	Д19:ÿ;

 

Заметим, что при доказательстве вовсе не использовалось свойство A2 группы (для каждого элемента группы существует обратный элемент).

 

Логическое программирование

В первом приближении логическое программирование - это использование дедуктивных процедур (процедур логического вывода) как механизма вычислений. Языки логического программирования являются декларативными в отличие от обычных “процедурных” языков”. В них в виде логических аксиом формулируются сведения о задаче и предположения, достаточные для ее решения. Сама задача формулируется как целевое утверждение, подлежащее доказательству. Таким образом, программа представляет собой множество аксиом, а вычисление - это конструктивный вывод целевого утверждения из программы. В логическом программировании (мы будем говорить о языке ПРОЛОГ) используется только одно правило вывода - резолюция.

Резолюция обладает важными свойствами - корректностью и полнотой. Резолюция корректна в том смысле, что если с ее помощью из множества формул S={F₁,...,F_k} и отрицания формулы R выводится пустой дизъюнкт, то справедливо F₁F₂...F_kÞR. Резолюция является полной в том смысле, что если R является логическим следствием множества формул S, то пустой дизъюнкт обязательно выводится из F₁F₂...F_kØR. Однако, в 1936 году Черчем и Тьюрингом было доказано, что для логики предикатов не существует разрешающего алгоритма для проверки общезначимости (и, следовательно, невыполнимости) формул. Поэтому запустив процесс логического вывода, в общем случае мы не можем сказать, завершится ли он. Если R не является логическим следствием формул S, то алгоритм доказательства может никогда не завершиться в случае, если существует бесконечное число возможных резольвент, последовательно получаемых в процессе выполнения алгоритма доказательства. Однако, для предикатов с конечной областью определения, и тем более в логике высказываний, не только положительный, но и отрицательный ответ на вопрос о невыполнимости логической функции всегда будет получен методом резолюции в конечное время (за конечное число шагов).

Логический вывод в Прологе

Логика предикатов и понятие логического вывода были разработаны в первой половине нашего века, но только в конце 60-х были поняты огромные возможности логического вывода для построения непроцедурных алгоритмов, тогда же и были разработаны методы резолюции, алгоритм унификации, и в конце концов язык логического программирования ПРОЛОГ. Основной вклад в логическое программирование был сделан Аланом Робинсоном (Alan Robinson), Алайном Колмерауером (Alain Colmeraurer) и Робертом Ковальски (Robert Kowalski), причем он был сделан сравнительно недавно. В этом языке исходное множество формул, для которого ищется пустая резольвента, представляется в виде так называемых “ дизъюнктов Хорна ”. Хорновские дизъюнкты - это формулы одного из трех типов:

отрицание: Ø(В1,...,Вn)

факт: А

импликация (правило): АÜ(В1,...,Вm),

где А, В₁,... - литеры - атомные высказывания или предикаты с отрицаниями или без них в нормальной предваренной форме только с (подразумеваемыми) кванторами всеобщности для всех переменных. Как мы видели из предыдущих разделов, любую логическую формулу можно привести к такому виду. Факты можно рассматривать как импликации, не имеющие посылок (антецедентов). Отрицания - как импликации, не имеющие следствий (консеквентов). Поэтому все дизъюнкты Хорна - это формулы вида АÜ(В₁,...,В_m), которые просто являются другой записью импликации В₁&...&В_mÞА, и знак Ü здесь может читаться как " при условии, что ". Все эти формулы представляются в виде дизъюнктов: ØВ₁Ú...ÚØВ_mÚА, или просто множеством литер {А,ØВ₁,...,ØВ_m}, поскольку знак дизъюнкции подразумевается. Именно к этим дизъюнктам и применяются последовательные шаги метода резолюции.

Таким образом, все задачи логического вывода можно формулировать, пользуясь только дизъюнктами Хорна, и все те задачи, которые являются в принципе разрешимыми, можно решить с помощью метода резолюции. Рассмотрим несколько примеров из [GL88].

Пусть в нотации, близкой языку ПРОЛОГ, записана программа:

Программа_1::

1: птица(Х) Ü откладывает_яйца(Х), имеет_крылья(Х)

2: рептилия(Х) Ü откладывает_яйца(Х), имеет_чешую(Х)

3: откладывает_яйца(ворона)

4: откладывает_яйца(питон)

5: имеет_чешую(питон)

6: имеет_крылья(ворона)

7:?птица(ворона)

В первой строке стоит правило, которое можно понять так: любое животное является птицей при условии, что оно откладывает яйца и имеет крылья. Очевидно, что это просто предикат в предваренной нормальной форме с опущенным квантором всеобщности (потому здусь и следует читать: любое животное). Этот предикат задан здесь одним дизъюнктом (птица(Х), Øотладывает_яйца(Х), Øимеет_крылья(Х)), где атомные предикаты дизъюнкта просто перечисляются через запятую вместо того, чтобы перечисляться через знак дизъюнкции. Вторая строка - это правило, аналогично определяющее класс рептилий. Третья строка - “откладывает_яйца(ворона)” - это, факт, который мы считаем истинным. Часто подобные факты присоединяются к программе из базы данных. Последняя строка - это утверждение-вопрос, истинность которого процессор языка ПРОЛОГ пытается проверить с помощью метода резолюции, пользуясь фактами и правилами.

Стратегии

В любом не «игрушечном» логическом выводе мы сталкиваемся с «комбинаторным взрывом» числа возможных резолюций, поскольку обычно база данных может содержать огромное множество фактов, не обязательно относящихся к данному конкретному вопросу, и построение всех возможных резольвент в этой базе данных бессмысленно. Поэтому при автоматизации логического вывода важнейшей проблемой является проблема выбора родительских дизъюнктов и их членов для унификации. Этот выбор должен выполняться так, чтобы пустая резольвента находилась скорейшим образом. Разработано несколько стратегий такого выбора, хотя общего метода, дающего оптимальное число шагов вывода для любой задачи, не существует. Например, в качестве одной из стратегий может применяться метод выбора на каждом шаге в качестве одного из родительских дизъюнктов такого дизъюнкта, который содержит только один дизъюнктивный член.

Выполнение программы на ПРОЛОГЕ следует другой стратегии: отрицание вопроса программы принимается за цель. Далее вычисляются резольвенты, порождаемые целью и каким-либо правилом или фактом, которые просматриваются последовательно сверху вниз. Если резольвента существует при наиболее общей унификации, она вычисляется. Если пустая резольвента с помощью такой стратегии не найдена, то ответ на вопрос отрицателен. В нашем примере резольвентой утверждений: Øптица(ворона) и птица(Х)Üоткладывает_яйца(Х),имеет_крылья(Х) является дизъюнкт, включающий отрицания двух утверждений: отладывает_яйца(Х) и имеет_крылья(Х). Эта пара становится новой целью, для которой снова ищется резольвента. Очевидно, что если в процессе вычислений найдена пустая резольвента, ответ на заданный вопрос утвердительный. Результатом программы на ПРЛОГЕ являются также и значения переменных, конкретизированные алгоритмом унификации в процессе вычислений - т.е. те значения параметров. при которых справедливо заключение. В примерах далее будем использовать прописные буквы для обозначения переменных, а строчные буквы - для имен конкретных объектов универсума.

Рассмотрим вычисление Программы 1:

 

 

Получение пустой резольвенты означает успех вычисления. Фактически, стоящий перед атомным предикатом знак вопроса означает вхождение этого предиката в дизъюнкт со знаком отрицания, и каждый такой дизъюнкт представляет собой очередную цель, которую нужно достичь (как бы проверить ее истинность).

Рассмотрим вычисление этой же программы с другой целью: 7:?птица(Х), что означает " Существует ли (произвольная) птица?". Пользователя обычно интересует не только сам факт успешного вычисления программы, но и конкретное значение переменной Х, при котором это возможно:

 

 

Заметим, что здесь цель вычисления была достигнута при нахождении единственного примера, который ему удовлетворяет. В общем случае может быть необходимо найти все такие конкретизации, удовлетворяющие цели, т.е. процессор Пролога должен пытаться найти все возможные резольвенты-продолжения. Рассмотрим следующий пример.

Программа_2::

1: Grandparent(X,Y) Ü Parent(X,Z), Parent(Z,Y)

2: Parent(elizabeth, charles)

3: Parent(charles, william)

4: Parent(charles, henry)

 

Содержательный смысл утверждений здесь очевиден. В качестве цели может быть выбрана любая из следующих:

5-а:?Grandparent(elizabeth, henry);

5-b:?Grandparent(elizabeth, V);

5-c:?Grandparent(U, henry);

5-d:?Grandparent(U, V).

Рассмотрим все возможные вычисления программы 2 при цели 5-d:

 

 

В качестве последнего примера из [GL88] рассмотрим логическую программу сортировки списка. Будем считать, что если у списка L выделены начальный элемент (голова) H и весь остальной список Т (хвост), то список L будем записывать как L=H:T.

Первый оператор логической программы сортировки списка определим как утверждение, которое определяет сортировку списка как результат подходящей вставки головы списка в отсортированный хвост списка:

1. Sort(H:T,S)ÜSort(T,L),Insert(H,L,S)

Смысл этого утверждения следующий: " список S является результатом сортировки списка H:T, если L является результатом сортировки списка T и S есть результат вставки элемента H в подходящее место списка L ". Это определение справедливо для всех списков, кроме пустых; этот частный случай можно учесть указанием конкретного факта: пустой список уже отсортирован:

2. Sort([],[])

Теперь мы должны определить, что означает операция Insert(Х,L,S)вставки элемента Х в отсортированный список L с получением отсортированного списка S. В случае, если этот элемент Х предшествует первому элементу списка L, то список S строится добавлением Х в качестве новой головы L:

3. Insert(X,H:T,X:H:T) Ü Precedes(X,H)

Это утверждение имеет следующий смысл: " Если элемент X предшествует по порядку элементу Н, то результатом вставки X в отсортированный список H:T является отсортированный список X:H:T ".

Если элемент H предшествует элементу X в списке H:T, то этот случай можно описать так:

4. Insert(X,H:T,H:T1) Ü Precedes(X,H), Insert(X,T,T1)

что можно интерпретировать так: " Результатом вставки X в отсортированный список H:T является список H:T1, если H предшествует X и T1 является отсортированным списком, получаемым после вставки X в отсортированный список T".

Кроме того, следует определить вставку элемента в пустой список:

5. Insert(X,[],[X]).

Таким образом, полная программа сортировки списка имеет пять операторов - утверждений:

Программа_3::

1. Sort(H:T,S) Ü Sort(T,L), Insert(H,L,S)

2. Sort([],[])

3. Insert(X,H:T,X:H:T) Ü Precedes(X,H)

4. Insert(X,H:T,H:T1) Ü Precedes(X,H), Insert(X,T,T1)

5. Insert(X,[],[X]).

Эту программу мы можем использовать многими различными способами, задавая различные цели. Например, "?Sort([dog cat pig], [cat dog pig])". При этой цели вычисление проверит, действительно ли список [cat dog pig] является отсортированной версией списка [dog cat pig]. При цели: "?Sort([dog cat pig], S)" вычислитель Пролога поместит в переменную S отсортированный список [dog cat pig]. При цели: "?Sort(S, [cat dog pig])" в переменную типа список S будут подставляться все перестановки элементов отсортированного списка [dog cat pig].