
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Трехзначная система РейтингаСодержание книги
Поиск на нашем сайте
В двузначной логике из закона исключенного третьего выводятся: 1) 1 (табл. 15, 16). Таблица 15 Отрицание Гейтинга
Таблица 16 Импликация Гейтинга
1) [Сху]=1,если 2) [Сху] = [у],если Конъюнкция и дизъюнкция определены обычным способом как минимум и максимум значений аргументов. Если учитывать лишь значения функций 1 и 0, то из матриц системы Гейтинга вычленяются матрицы двузначной логики. В этой трехзначной логике закон непротиворечия является тавтологией, но ни закон исключенного третьего, ни его отрицание тавтологиями не являются. Оба правильных модуса условно-категорического силлогизма, формула Хотя по сравнению с логикой Лукасевича в матрицах отрицания и импликации Гейтингом в его системе были произведены небольшие изменения, результаты оказались значительными: в системе Гейтинга являются тавтологиями многие формулы классического двузначного исчисления высказываний.
Трехзначная система Бочвара30 Система советского логика Д. А. Бочвара построена на разделении высказываний на имеющие смысл (т. е. истинные или ложные) и бессмысленные. Бочвар выделяет внешние формы (или функции) и внутренние. Внутренние формы Бочвар называет классическими содержательными функциями переменных высказываний, а внешние формы — не классы чески ми. У Бочвара «истина» обозначается Л, «ложь» — F, «бессмысленность» — S. Мы обозначим «истину» как 1, «ложь» — 3, «бессмысленность» — 2. Тавтология принимает значение 1; а, Ь, с... обозначают переменные высказывания. В настоящей работе не приводится полное определение функций (в силу его сложности). Бочвар ввел два вида отрицания — внутреннее и внешнее, которые определяются таблично, В системе Бочвара ни закон тождества двузначной логики, ни его отрицание не являются тавтологиями. Отрицание закона тождества сыграло важную роль при анализе парадокса Рассела. Бочвар же не отбрасывает принцип «а есть а» или Противоречиями в логике Бочвара являются следующие формулы: 1) Бочвар построил свое трехзначное нечисление с целью разрешения парадоксов классической математической логики методом формального доказательства бессмысленности определенных высказываний. В частности, с помощью своей системы Бочвар смог разрешить парадокс Рассела о множестве всех нормальных множеств, доказав несуществование такого предмета, как множество всех нормальных множеств. В действительности это означает, что, поскольку предметная область состоит из фиксированных предметов, о которых можно рассуждать по законам классической формальной логики, множество всех нормальных множеств нельзя рассматривать как фиксированный предмет, не изменяющийся в то время, пока о нем идет речь. Система Бочвара позволяет элиминировать парадокс Рассела, не прибегая к теории типов.
n -значная система Поста31 Система Поста является обобщением двузначной логики, ибо при л=2 в качестве частного случая мы получаем двузначную логику. Своей системе Пост дал интерпретацию. Значения истинности суть 1, 2,..., л Пост вводит два вида отрицания (N*x и N1x)y соответственно называемые циклическим и симметричным. Они определяются путем матриц и посредством равенств. Первое отрицание определяется двумя равенствами: 1. LY1x]=M+l при 2. [^п]=1. Второе отрицание определяется одним равенством: [N2x]=n-[x] + \. Матрица, определяющая первое и второе отрицания, имеет вид табл. 17.
Таблица 17
Характерной особенностью двух отрицаний Поста является то, что при л=2 эти отрицания совпадают между собой и с отрицанием двузначной логики, что подтверждает тезис: многозначная система Поста есть обобщение двузначной логики. Конъюнкция и дизъюнкция определяются соответственно как максимум и минимум значений аргументов. При указанных определениях отрицания, конъюнкции и дизъюнкции обнаруживается, что при значении для х, большем двух, законы непротиворечия и исключенного третьего, а также отрицания этих законов не являются тавтологиями. Если значениями истинности являются 1, 2, 3, то из n -значной системы Поста вычленяется трехзначная логика, т. е. Ръ. Аналогично при значениях истинности 1, 2, 3, 4 получается четырехзначная логика Р4 и т. д. Трехзначная система Р3 Поста имеет следующую форму (табл. 18, 19).
В этих таблицах приняты обозначения, введенные Постом при n- 3:первое отрицание обозначается через Если в качестве значений истинности взяты лишь 1 «истина» и 3 «ложь», то из таблиц системы Р 3 Поста вычленяются таблицы для отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции двузначной логики. В системе Рэ тавтология принимает значение 1; закон исключенного третьего не является тавтологией ни для первого, ни для второго отрицания Поста, но является тавтологией закон исключенного четвертого для первого отрицания.
Трехзначная система Рейхенбаха32 Аппарат многозначных логик находит все более широкое применение в различных науках. Проанализируем применение аппарата трехзначной логики Г. Рейхенбаха к квантовой механике. Большинство операций этой системы было введено уже Постом, но с целью приложения своей системы к квантовой механике Рейхенбах вводит новые. У Поста было введено два вида отрицания — первое и второе. В системе Рейхенбаха они называются циклическим отрицанием и диаметральным отрицанием, кроме них Рейхенбах ввел полное отрицание. В системе Рейхенбаха имеются стандартная импликация Таблица для трех видов отрицаний Рейхенбаха. Обозначения:
Рейхенбах обозначил «истину» как 1, «неопределенность» — 2, «ложность» — 3. Тавтология принимает значение 1 (табл. 20). Таблица 20
Другие функции Рейхенбаха определяются матрицами так (табл. 21).
Отметим ряд свойств, присущих отрицаниям в системе Рейхенбаха. Для циклического отрицания верен закон снятия тройного отрицания: А возвращаемся к исходному значению А. Для циклического отрицания законы непротиворечия и исключенного третьего, правила де Моргана двузначной логики не являются тавтологиями, но тавтологией является закон исключенного четвертого:
Для диаметрального отрицания сохраняется правило снятия двойного отрицания: Для полного отрицания оказались тавтологиями закон непротиворечия, псевдозакон исключенного третьего, закон исключенного четвертого, правила де Моргана, закон Рассмотрев три вида отрицания в их взаимосвязи, Рейхенбахпоказал, что между циклическим и полным отрицанием имеет место следующее отношение:
Ранее отмечалось, что для циклического отрицания является тавтологией закон исключенного четвертого:
Вследствие этой двусмысленности для полного отрицания нельзя определить обратной операции, т. е. операции, ведущей от Взаимосвязь трех видов отрицания выражается в том, что закон непротиворечия сохраняется в таких трех формах: 1) Рейхенбах построил свою трехзначную систему для описания явлений квантовой механики. По его мнению, говорить об истинности или ложности высказываний правомерно лишь тогда, когда возможно осуществить их проверку. Если нельзя ни подтвердить истинность Высказывания (т. е. верифицировать его), ни опровергнуть его с помощью проверки (фальсифицировать), то такое высказывание должно оцениваться третьим значением — неопределенно. К числу таких высказываний относятся высказывания о ненаблюдаемых объектах в микромире. Сам Рейхенбах так пишет о значении трехзначной логики для квантовой механики: «Введение третьего значения истинности не делает все высказывания квантовой механики трехзначными. Рамки трехзначной логики достаточно широки, чтобы включать класс истинно-ложных формул. Когда мы хотим все высказывания квантовой механики ввести в состав трехзначной логики, то руководящей идеей будет: поместить в истинно-ложный класс те высказывания, которые мы называем законами квантовой механики»33.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.72 (0.009 с.) |

 2)
2)  Исходя из утверждения, что истинным является лишь второе, Гейтинг разработал трехзначную пропозициональную логику. В этой логической системе импликация и отрицание отличаются от определений этих операций у Лукасевича лишь в одном случае. «Истина» обозначается 1, «ложь» — 0, «неопределенность» — 1/2. Тавтология принимает значение
Исходя из утверждения, что истинным является лишь второе, Гейтинг разработал трехзначную пропозициональную логику. В этой логической системе импликация и отрицание отличаются от определений этих операций у Лукасевича лишь в одном случае. «Истина» обозначается 1, «ложь» — 0, «неопределенность» — 1/2. Тавтология принимает значение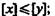

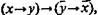 правила де Моргана и закон исключенного четвертого:
правила де Моргана и закон исключенного четвертого:  — тавтологии.
— тавтологии.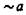 — внутреннее отрицание,
— внутреннее отрицание,  — внешнее отрицание,
— внешнее отрицание, 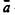 — внутреннее отрицание внешнего утверждения.
— внутреннее отрицание внешнего утверждения.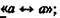 в его системе формулане
в его системе формулане  является доказуемой.
является доказуемой.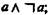 2)
2) 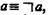 3)Здесь знак
3)Здесь знак  означает
означает 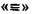 внешнюю равнозначность (эквивалентность), знак
внешнюю равнозначность (эквивалентность), знак  — внешнюю равносильность.
— внешнюю равносильность. где л — конечное число. Тавтологией является формула, которая всегда принимает такое значение i, что
где л — конечное число. Тавтологией является формула, которая всегда принимает такое значение i, что  где
где  значения 1,..., S называются выделенными или отмеченными; возможно, что
значения 1,..., S называются выделенными или отмеченными; возможно, что 


 второе отрицание — через
второе отрицание — через  конъюнкция — через
конъюнкция — через  дизъюнкция — через
дизъюнкция — через 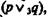 импликация — через
импликация — через  эквиваленция — через
эквиваленция — через 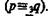
 и стандартная эквивалентность
и стандартная эквивалентность  Вводятся и другие операции: альтернативная импликация
Вводятся и другие операции: альтернативная импликация 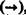 , квазиимпликация
, квазиимпликация  и альтернативная эквивалентность
и альтернативная эквивалентность  Знаком «•» обозначена конъюнкция, —дизъюнкция.
Знаком «•» обозначена конъюнкция, —дизъюнкция. 
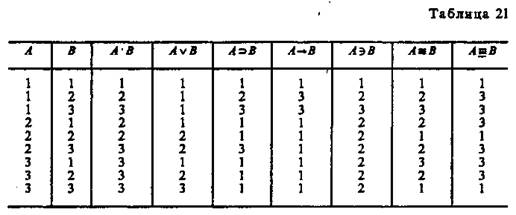
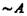 — циклическое отрицание; — А — диаметральное отрицание;
— циклическое отрицание; — А — диаметральное отрицание; 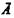 — полное отрицание.
— полное отрицание.
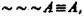 т. е. в результате тройного отрицания
т. е. в результате тройного отрицания
 Ни сами законы непротиворечия и исключенного третьего, ни их отрицания при диаметральном отрицании не являются тавтологиями.
Ни сами законы непротиворечия и исключенного третьего, ни их отрицания при диаметральном отрицании не являются тавтологиями.
 (1)
(1) Последние два члена его можно заменить на основании равенства (1) на
Последние два члена его можно заменить на основании равенства (1) на  и получить для полного отрицания формулу
и получить для полного отрицания формулу  которую Рейхенбах назвал «псевдозаконом исключенного третьего», ибо он не имеет свойств закона исключенного третьего двузначной логики. Причина последнего в том, что полное отрицание не имеет свойств обычного отрицания: оно не дает нам возможности определить значение истинности А, если мы знаем, что
которую Рейхенбах назвал «псевдозаконом исключенного третьего», ибо он не имеет свойств закона исключенного третьего двузначной логики. Причина последнего в том, что полное отрицание не имеет свойств обычного отрицания: оно не дает нам возможности определить значение истинности А, если мы знаем, что 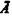 истинно. Из табл. 22, определяющей полное отрицание, следует, что если
истинно. Из табл. 22, определяющей полное отрицание, следует, что если 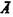 истинно, то А может быть как ложным, так и неопределенным.
истинно, то А может быть как ложным, так и неопределенным.
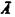 к А.
к А.



