
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о логической форме мысли и логическом законе. Предмет логикиСодержание книги
Поиск на нашем сайте
ПОНЯТИЕ О ЛОГИЧЕСКОЙ ФОРМЕ МЫСЛИ И ЛОГИЧЕСКОМ ЗАКОНЕ. ПРЕДМЕТ ЛОГИКИ Логика (греч. «логос») – понятие, разум, рассуждение: 1. Объект. логика – закономерности в изменении и развитии вещей и явлений объективного мира 2. Субъект. логика – особ. закономерности в изменении в связях и развитии мыслей 3. Наука о закономерностях в связях и развитии мыслей
Логика – наука о мышлении.
Познание – отражение (не зеркальное) объект. реальности в сознании ч-ка: 1. 1-ая ступень: Чувственное познание – отражение (непосред.) действительности посредством органов чувств в виде ощущений, восприятий, представлений. С помощью этих видов отражения не удаётся познавать внут., существенные стороны вещей и явлений, з-ны их ф-ционирования и развития 2. 2-ая ступень: Абстрактное мышление (лог. познание) – отражение (опосред.) действительности путём лог. переработки чувственных данных. Исходя из чувственных данных: · Мы можем познавать то, чего не наблюдаем непосредственно · В предметах и явлениях выделяют общие св-ва и на их основе выделяют и обобщают предметы нек. типа, в результате чего образуются понятия об этих предметах
Метод логики – понятия о предметах.
Обобщающий хар-р мышления – возможность формировать з-ны.
Мышление – актив. и целенаправ. деят-ь. В процессе мышления ставятся определённые цели и формируются задачи. Для их достижения и решения осуществляются мыслительные действия.
Предмет логики: 1. Формы мыслей и формы развития знания 2. Особые приёмы и методы познания, применяемые на ступени абстрактного мышления 3. Особые з-ны мышления
Лог. термины – термины, кот. выражают наиболее общие хар-ки вещей и явлений, а также мыслей: «и», «или», «если …, то …», «неверно, что» («не»), «все» («ни один»), «суть» («есть»), «следовательно» и др.
Процесс выявления лог. формы мысли – отвлечение от смысла нелог. терминов, входящих в словосочетание, выражающее эту мысль.
Лог. форма мысли (процесса мышления) – структура мысли, выявляемая в результате частичного отвлечения от смыслов и значений нелог. терминов, входящих в словосочетание, выражающее эту мысль (процесс мышления).
Частичное отвлечение – сохранение информации о типе терминов, от кот. произошло отвлечение, и о том, где находился один и тот же термин, а где разные.
Классы мыслей: 1. Понятие – мысль, в кот. обобщены в класс и выделены из нек. множества предметы на основе системы признаков, общей только для этих обобщённых и выделенных предметов 2. Суждения – мысли, в которых утверждается наличие или отсутствие к/л положений дел 3. Умозаключение – процесс получения знания, выраженного в суждении, из др. знаний, тоже выраженных в суждениях
Лог. законы (формально-лог. з-ны) – связи между мыслями по формам, при кот. истинность одних из этих мыслей обуславливает истинность др.
Чтобы установить, является ли связь между нек. исходными высказываниями и высказыванием, получаемым в результате рассуждения, лог. законами, необходимо вместо нелог. терминов подставлять в эти высказывания произвольные термины тех же типов и при этом всякий раз выяснять, окажется ли истинным получаемое высказывание при истинности исходных.
Все преступники подлежат уг. от-ти Нек. жители Чикаго подлежат уг. от-ти Нек. жители Чикаго – преступники Все студенты 2-го курса юрфака сдают логику Нек. студенты МГУ сдают логику Нек. студенты МГУ – студенты 2-го курса юрфака
Формальная логика – наука о формах мыслей, о формально-лог. з-нах и др. связях и отношениях между мыслями по их лог. формам.
ОСНОВНЫЕ ЭТАПЫ РАЗВИТИЯ ЛОГИКИ. ЗНАЧЕНИЕ ЛОГИКИ ДЛЯ ЮРИСТОВ
Значение логики для юристов: 1. Для повышения логической культуры: умение давать определения, классифицировать, строить аргументацию и опровержение 2. Ускоряет нахождение ошибок в ходе судебного заседания 3. Помогает строить судебно-следственные версии, составлять четкие планы расследования преступлений, составлять официальные документы: протоколы допроса и осмотра, рапортов и т.д. 4. Знание логических приемов позволяет направлять ход дискуссии на достижение истины 5. Для прогнозирования преступности и оценки деятельности правоохранительных органов 6. Для нормотворчества (логика норм)
Формальная логика — одна из самых др. наук. Она начала разрабатываться в Др. Греции в 6-5 вв. до н.э. Немного позже в Др. Индии. Греч. логика распространилась позднее в Запад. и Восточ. Европе и на Ближ. Востоке, а индийская — в Китае, Японии, Тибете, Монголии, на Цейлоне и в Индонезии.
Первоначально логика разрабатывалась в связи с запросами практики судопроизводства и ораторского искусства.
Часто суд. решение зависело от лог. доказательности речи обвиняемого или обвинителя.
Иногда при определении победителя дискуссии мнения присутствующих (или судей) разделялись. Одни считали победителем одного из ораторов, другие — другого. Это выдвинуло на повестку дня задачу разработать лог. нормы рассуждений, кот. позволяли бы избегать таких разногласий и приходить к единому мнению.
В Др. Греции логику разрабатывали Парменид, Зенон, Сократ, Платон. Однако основателем науки логики считается Аристотель. Он написал “Органон” (орудие познания).
Поскольку логика разрабатывалась древними авторами в качестве руководства для ведения дискуссий, она часто называлась диалетикой (от греческого слова “диалего” — “спорю”). После Аристотеля в Др. Греции логика разрабатывалась стоиками.
Средневековая логика называется схоластической. Её расцвет относят к 14 в. и связывают с именами Уильяма Оккама, Уолтера Бёрли, Альберта Саксонского
Логика развивалась в эпоху Возрождения и Новое время. Френсисом Бэконом написан “Новый Органон”, в котором содержались основы индуктивных методов, усовершенствованных позже Джоном Стюартом Миллем и получившие название методов установления причинных связей между явлениями (методов Бэкона-Милля).
Логика, основанная на учении Аристотеля, во многом дополненная и развитая, существовала до начала 20 в. В нач. 20 в. в логике произошла своеобразная научная революция, связанная с широким применением методов так называемой символической, или математической логики. Идеи последней высказаны нем. ученым Г.В. Лейбницем. Идея Лейбница о возможности и продуктивности сведения рассуждении к вычислениям в течение многих лет не находила развития и применения.
Символическая логика начала создаваться лишь в середине 19 в. Таким образом, к началу текущего столетия символическая логика оформилась в качестве относительно самостоятельной дисциплины в рамках логической науки. Именно использование методов символической логики отличает логику современную от традиционной. Вместе с тем в современной логике сохраняются все достижения и вся проблематика традиционной логики.
Диалектическая логика также имеет древнее происхождение. Идеи диалектики мышления восходят к древневосточной и античной философии. В развитие диалектической логики внесли определенный вклад Платон и Аристотель, Классические формы диалектической логике придали немецкие философы Нового времени: Кант, Фихте, Шеллинг и, в особенности, Гегель. Диалектическую логику на материалистической основе разрабатывали К. Маркс, Ф. Энгельс и В.И. Ленин. Дальнейшее развитие она получила в трудах современных философов.
УЧЕНИЕ ЛОГИКИ ОБ ИМЕНАХ
Имя – один из видов знаков; слово/словосочетание, обозначающее к/л предмет. Учение об именах – теория именования.
Т.к. имя – знак, то оно имеет значение: 1. Предметное (может не иметь) – предмет обозначаемый этим именем 2. Смысловое (обязательно имеет): · Смысл – (концепт) – выраженная в языке информация о предметах, кот. позволяет однозначно выделять предметы, являющиеся значением имени · Идея – зрит. образ (интуит. представление) предметов, обозначаемых именем
Типы имён: 1. Единичные имена – обозначают 1 предмет (напр., Луна, столица России): · Значение – единственный предмет 2. Общие имена – имена, общие для предметов нек. класса (напр., преступление против соб-ти, европ. гос-во): · Значения – предметы нек. класса, содержащего более 1 элемента
Объём имени – класс, кот. составляют предметы: 1. У единичного имени – класс, состоящий из 1 предмета 2. У общего имени – класс, состоящий из неск. предметов · Универсальные имена – общие имена, объёмом кот. явл. весь универсум рассуждения – вся область предметов, о кот. ведётся рассуждение (напр., «ч-к, знающий нек. ин. языки или не знающий ни одного ин. языка» универсум – все люди). Универсум рассуждения определяется контекстом, в кот. употребляется имя
Могут быть имена с разными смыслами и одним и тем же объёмом (напр., «самый большой город Англии» и «столица Англии»), но не может быть имён с одним и тем же смыслом, но разными объёмами.
1. Мнимые имена – имена, обозначающие предметы, не существующие в универсуме рассуждения (напр., русалка, вечный двигатель): · Универсум рассуждения – предметы, существующие в объективной реальности · Объём имени – пустое множество 2. Действительные имена – имена, значениями которых явл. предметы, входящие в универсум рассуждения
Осн. методологические принципы употребления имён: 1. Принцип однозначности: · Если единичное имя – выражение, используемое в качестве имени, должно быть именем только 1 предмета · Если это общее имя – выражение должно быть именем, общим для предметов 1 класса 2. Принцип взаимозаменимости – если в слож. имени заменить часть, в свою очередь являющуюся именем, др. именем с тем же значением, то значение полученного в результате такой замены слож. имени должно быть тем же, что и значение исходного слож. имени (напр., в предложении «Земля вращается вокруг Солнца» заменим имя «Солнце» на имя «центральное тело Солнечной системы» => значения этих имён совпадут) 3. Принцип предметности – в высказываниях должно утверждаться/отрицаться нечто о значениях имён, входящих в предложения, а не о самих именах. · Кавычковые имена - значениями нек. имён могут являться имена. Такие случаи не противоречат принципу предметности (напр., в предложении «Материя первична, а сознание вторично» «материя» - это имя объект. реальности, а в предложении ««Материя» - философ. категория» «материя» - это имя имени, имя категории) · Автонимное употребление имён - именем имени является само исходное имя (напр., в предложении «Слово стол состоит из 4 букв» слово «стол» является именем самого этого слова)
Способы употребления имён: 1. Имя просто выделяет предмет (предметы) 2. Предметы, обозначаемые именем, рассматриваются в определённом аспекте · Если имя употребляется в этом смысле, то его можно заменять др. именем с тем же значением, если только во 2-ом имени предметы рассматриваются в том же аспекте (напр., указанную замену можно было бы произвести, если бы Птолемей считал, что значения имён «Солнце» и «центральное тело Солнечной системы» совпадают => «Птолемей считал, что Солнце вращается вокруг Земли» - ложь)
СЛОЖНЫЕ СУЖДЕНИЯ
Слож. суждение – суждение, в кот. можно выделить часть, являющуюся суждением.
Способ образования: 1. Из прост. и слож. суждений 2. С помощью: · Лог. союзов (если…, то…; или; и) · Отрицания (неверно, что…) · Модальных терминов (возможно, что…; необходимо, что…; случайно, что…) · И т.д.
1. Соединительные суждения – суждения, в кот. утверждается наличие 2 или более ситуаций (напр., Понятые присутствуют и протокол составляется).
Чаще всего такие утверждения выражаются посредством предложений, содержащих союз «и». Он обозначается символом «&», называется знаком (неопределённой) конъюнкции. Суждения с этим союзом – (неопределённо) конъюнктивные. А & B – форма конъюнктивного суждения.
Последовательно-конъюнктивные суждения – суждения, в кот. утверждается последовательное возникновение или существование 2 или более ситуаций. Они образуются из 2 или более суждений, при помощи союзов, обозначаемых символами (знаками последовательной конъюнкции) А
Одновременно-конъюнктивные суждения ( А
2. Разделительные суждения – суждения, в кот. утверждается наличие 1 из 2, 3 и т.д. ситуаций: 1. Дизъюнктивное суждение ((нестрого) разделительное, соединительно-разделительное) – утверждается наличие по крайней мере 1 из 2 ситуаций (v – или – (нестрогая) дизъюнкция)
2. Строго-дизъюнктивное суждение (строго-разделительное) – утверждается наличие ровно 1 из 2 или более ситуаций (v – или…, или… - строгая дизъюнкция) – истинно только тогда, когда истинно только 1 суждение из составляющих его суждений ·
3. Условные суждения – суждения, в кот. утверждается, что наличие одной ситуации обуславливает наличие другой (→ - если…, то…): 1. Необходимое условие для данного события – при его отсутствии это событие не происходит (Наличие кислорода является необходимым условием для того, чтобы огонь продолжал гореть) 2. Достаточное условие для данного события – всякий раз, когда имеется это условие, событие происходит (Выпадение дождя является достаточным условием для того, чтобы крыши домов были мокрыми)
Виды условий: 1. Достаточные, но не необходимые (Делимость числа N на 10 является достаточным, но не необходимым условием его делимости на 2) 2. Необходимые, но не достаточные (Делимость числа N на 2 является необходимым, но не достаточным условием его делимости на 6) 3. Необходимые и достаточные (Делимость числа N на 2 и 3 является необходимым и достаточным условием его делимости на 6)
В условном суждении: 1. Основание – часть между «если» и «то» (антецендент) 2. Следствие – часть после «то» (консеквент) Условное суждение – суждение, в кот. ситуация, описываемая основанием является достаточным условием для ситуации, описываемой следствием.
Контрафактическая связь (•→) – ситуация, описываемая основанием, не имеет места, но если бы она существовала, то существовало бы следствие (Если бы Иванов был президентом, то не ездил бы в общественном транспорте).
4. Суждения эквивалентности – суждения, в кот. утверждается взаимная обусловленность 2 ситуаций (↔ - если и только если…, то… (тогда и только тогда…, когда…)): 1. Основание – достаточное и необходимое условие для ситуации, описываемой следствием (Если и только если солнце находится в зените, то тени от него являются самыми короткими) 2. Следствие - достаточное и необходимое условие для ситуации, описываемой основанием
5. Суждения с внеш. отрицанием – суждения, в кот. утверждается отсутствие нек. положения дел ((знак отрицания)- неверно, что…;не).
6. (Алетические) Модальные суждения –суждения, образованные из др. суждений путём хар-ки описываемых в них положений дел в качестве: 1. Необходимых 2. Случайных 3. Возможных
Атрибутивные и суждения об отношениях – ассерторические суждения. Они являются (просто) утверждениями или отрицаниями. На ряду с ними выделяют сильные и слабые утверждения и отрицания, которые являются модальными суждениями.
Понятия «необходимо», «случайно», «возможно» - алетические модальные понятия (модальности).
Модальности: 1. Логические - положение дел может быть логически: · Возможно (M) - то, что не противоречит з-нам логики. Не все то, что лог. возможно, возможно фактически (Мы знаем, что жизнь на Луне невозможна (фактически), но утверждение “На Луне есть жизнь” не противоречит законам логики, следовательно, логически возможно, что на Луне есть жизнь) · Необходимо (L) - то, что является з-ном логики · Случайно (C) 2. Фактические (онтологические) - положение дел может быть фактически: · Возможно (◊) - то, что не противоречит законам природы и общественной жизни · Необходимо (□) – з-ны природы и общественной жизни и лог. следствия из них · Случайно (∇)
Используя символы, можно выразить связь между алетическими модальностями: 1. M A ↔ ØL ØA 2. L A ↔ ØM ØA 3. С А ↔ М А & М ØА 4. ◊ A ↔ Ø□ ØA 5. □ A ↔ Ø◊ ØA 6. ∇ A ↔ ◊ A & ◊ ØA
ОТНОШЕНИЯ МЕЖДУ СУЖДЕНИЯМИ
Основными видами отношений между суждениями по лог. формам являются отношения: 1. Основные: · Совместимость по истинности – имеет место между суждениями A и B если и только если лог. формы этих суждений являются истинными. Если такие суждения не существуют, то между исходными суждениями имеет место отношение логической несовместимости по истинности · Совместимость по ложности - имеет место между суждениями А и В, если и только если существуют суждения этих же лог. форм, которые оба являются ложными. Если таковые не существуют, то суждения А и В находятся в отношении логической несовместимости по ложности · Лог. следование - имеет место между суждениями А и В (факт наличия этого отношения обозначается так: А |= В или А Þ В), если и только если не существуют суждения А' и В' тех же логических форм, что А' истинно, а В' ложно 2. Производные: · Лог. эквивалентность - имеет место между суждениями А и В, если и только если А Þ В и В Þ А. Оно обозначается так: А Û В. Если они следуют друг из друга · Подчинение – имеет место если и только если А |= В и В |¹ А. Знак “|¹” означает: “не следует”. Суждение А называется в этом случае подчиняющим, а В — подчиненным · Контрадикторность - имеет место между суждениями, которые несовместимы по истинности и несовместимы по ложности · Контрарность – имеет место, если суждения, совместимы по ложности, но несовместимы по истинности · Субконтрарность – имеет место, если суждения совместимы по истинности, но несовместимы по ложности · Лог. независимость – имеет место если и только если суждения совместимы по истинности и ложности и каждое из них не находится в отношении лог. следования к др. из этих суждений
ОТРИЦАНИЕ СУЖДЕНИЙ
Отрицание суждения - операция, заключающаяся в таком преобразовании лог. содержания суждения, в результате кот. получают суждение, находящееся в отношении контрадикторности (противоречия) к исходному.
При отрицании артибутивного суждения и суждений об отношениях меняются их качество и кол-во на противоположные.
При отрицании единичного суждения его кол-во не меняется.
Примеры: 1. Все юристы изучают логику, и все философы изучают логику – Нек. юристы не изучают логику, или нек. философы не изучают логику 2. Идёт дождь, или идёт снег – Нет дождя и нет снега
Последовательно конъюнктивное суждение ( Ø (A
Одновременно-конъюнктивное суждение ( Ø (A
Строго-дизъюнктивное суждение (v – или…, или…) отрицается по схеме: Ø (A v B) ↔ (A & B) v (ØA & ØB) Пример: Либо Иванов совершил это преступление, либо Иванов – Это преступление совершили Иванов и Петров, или не тот и не другой
Условное суждение (→ - если…, то…) отрицается по схеме: Ø (A → B) ↔ ◊ (A & ØB) Пример: Если ч-к закаляется, то он здоров – Возможно, что ч-к закаляется, но не является здоровым
Модальные суждения отрицаются по схемам: 1. Ø□ A ↔ ◊ ØA 2. Ø◊ A ↔ □ ØA 3. Ø∇A ↔ □ A v □ ØA
Лог. хар-ка.
Вопросы задают в тех случаях, когда есть познавательная неопределенность.
Вопрос – мысль, в кот. выражено пожелание дополнить имеющуюся информацию с целью устранения/уменьшения познавательной неопределённости.
Предпосылка вопроса – исходное знание (суждение/система суждений), явно/неявно содержащееся в вопросе: 1. Лог. – лог. знание, выраженное лог. формой вопросительного предложения 2. Факт. – знание, выраженное всеми терминами вопросительного предложения, а также всеми известными связями и св-вами предметов, о кот. идёт речь в вопрос. Предложении Предпосылка обуславливает множество возможных ответов на вопрос.
Характеризуя вопросы с лог. точки зрения, следует рассматривать вопросно-ответные ситуации, включающие предпосылки вопросов. Благодаря последним вопросы могут использоваться для неявной передачи информации. Напр., на чью сторону встанет армия, если будет предпринята попытка гос. переворота? – информация о том, что: 1. Попытка возможна 2. Возможно выступление армии на 1 из сторон
Тот факт, что вопросы имеют предпосылки, используется для совершения уловки «сокрытие необоснованности утверждения». Оно выражается не явно, а в виде предпосылки вопроса. Напр., чтобы обосновать целесообразность снижения налогов, властям задают вопрос: «Кода вы начнёте снижать налоги?»
Др. уловка, связанная с предпосылками вопросов – «подмена вопроса» - пользуясь тем, что одним и тем же вопросительным предложением могут быть выражены разные вопросы из-за различия в подразумеваемых или содержащихся в контекстах предпосылках, заданный вопрос заменяют другим, или же ответ на один вопрос выдают за ответ на другой. Напр., вопрос: «Собираетесь ли вы посетить места, где можно повеселиться ночью?» - ответ: «Здесь есть такие места?». Виды вопросов: 1. По числу ответов: · Открытые – вопросы, кот. не предполагают определённого числа ответов (как препод читает лекции?) · Закрытые – вопросы, кот. требуют определённое число ответов (как препод читает лекции – хорошо или плохо?) 2. Вопросы, между предпосылками которых имеет место отношение лог. следования (из предпосылки одного вопроса следует предпосылка другого: 1-ый – более информативный, чем другой): · Логически эквивалентные · Фактически эквивалентные 3. Вопросы, требующие устранения большей/меньшей неопределенности (вопрос, требующий устранения большей неопределённости, чем другой: 1-ый – более информационный, чем другой) 4. По составу: · Простые (кто организатор преступления?) · Сложные – вопросы, в кот. можно выделить часть, являющуюся вопросом (кто организатор преступления и где находится краденное?) 5. По правильности: · Логически корректные (правильные) – вопросы, на кот. можно дать истинный ответ, снижающий познавательную неопределённость · Логически некорректные (неправильные) - вопросы, на кот. нельзя дать истинный ответ и ответ, снижающий познавательную неопределённость: Ø v Бессмысленные – вопросы, в формулировке кот. содержатся выражения, ни смыслы, ни значения кот. не известны (или выражения, имеющие смысл, но между ними нет согласования) v Недоопределённые – вопросы, в формулировке кот. содержатся многозначные термины и из контекста не ясно, в каком из смыслов они употребляются Ø Провокационные – вопросы, на кот. можно дать только ложный прямой ответ. Предпосылками вопросов являются ложные суждения (перестал ли ты бить свою жену?) Ø Тавтологичные – вопросы, на кот. нельзя дать ответа, снижающего познавательную неопределённость, т.к. её нет: v Логически – запрашиваемая информация выражается лог. формой вопроса (является ли Иванов ч-ком, кот. он действительно является?) v Фактически - запрашиваемая информация выражается всеми терминами, входящими в формулировку вопроса, а не только его лог. формой (между кем и кем была Русско-японская война?)
Виды ответов: 1. · Бессмысленные - ответы, в формулировке кот. содержатся выражения, ни смыслы, ни значения кот. не известны (или выражения, имеющие смысл, но между ними нет согласования) · Недоопределённые - ответы, в формулировке кот. содержатся многозначные термины и из контекста не ясно, в каком из смыслов они употребляются 2. Ложные: · Противоречивые (подкова над дверью приносит удачу даже тем, кто в неё не верит) 3. Истинные: · Правильные – ответы, полностью (сильные) или частично (слабые) устраняющие познавательную неопределённость: Ø Полные – ответ на слож. вопрос, если он содержит ответы на все подвопросы Ø Неполные - ответ на слож. вопрос, если он не содержит ответы на часть подвопросов · Неправильные – ответы, не снижающие познавательной неопределённости: Ø Тавтологичные: v Логически - ответы, не несущие факт. информацию, поэтому не могут снижать познавательную неопределённость v Фактически – ответы, кот. полностью/частично повторяют предпосылку или общеизвестную информацию Ø Нерелевантные – ответы не на заданные вопросы 2. Прагматическая хар-ка – оценивать вопросы и ответы с точки зрения полезности. Расширительные вопросы. Напр., задавая вопрос в суде, адвокат не должен требовать устранения неопределенности, если это устранение усугубляет виновность подсудимого.
Нерелевантные вопросы – вопросы, не относящиеся к делу. Задача судьи — отклонять такого рода вопросы.
Избыточные ответы – ответы, снижающие не только выраженную в вопросе неопределённость, но и ту, кот. в вопросе не выражена. Напр., подсудимого спрашивают, знает ли он потерпевшего. Подсудимый отвечает, что не знал раньше потерпевшего, но знал его жену.
ЯЗЫК ЛОГИКИ ВЫСКАЗЫВАНИЙ. ТАБЛИЧНЫЕ ОПРЕДЕЛЕНИЯ ЛОГИЧЕСКИХ ТЕРМИНОВ
Одним из способов описания выводов логики высказываний является табличное построение логики высказываний.
Логика высказываний – раздел символической логики, поэтому в ней используется язык символов.
Символы этого языка: 1. p, q, r, s, p1, q1,... — пропозициональные символы (пропозициональные переменные, символы для суждений) 2. Ø, &, Ú, →, ↔ — лог. термины (лог. константы) 3. (,) — скобки
Определение формулы: 1. Пропозициональная переменная есть формула 2. Если А - формула и В - формула, то ØA, (А & В), (A Ú B), (А É В), (А º В) — формулы 3. Ничто иное не есть формула
Принимаются соглашения об опускании скобок в формулах. Опускаются внеш. скобки у отдельно стоящей формулы. Считают, что знак Ø связывает теснее, чем знаки &, v, É, º; знак & — теснее, чем v, É, º; знак v — теснее, чем É, º; знак É теснее, чем º.
При табличном построении логики высказываний лог. константы определяются посредством таблиц истинности. При этом принимается, что каждое высказывание имеет одно значение — или «истина», или «ложь».
Элементарная формула - формула, являющаяся пропозициональной переменной.
Слож. формула - формула, содержащая лог. константы. В слож. формуле можно выделить лог. константу, называемую глав. лог. константой формулы.
Каждую сложную формулу логики высказываний можно единственным образом представить в виде: 1. Ø А 2. А & В 3. A v В 4. А É В 5. А º В А и В - формулы, являющиеся частями слож. формулы. Подформулы, конечно, в свою очередь могут быть слож. формулами.
Напр., ((Øp v q) É (р & Øq)).
Представив таким образом слож. формулу, мы выделяем в ней последнюю по построению лог. константу – глав. лог. константу формулы.
1.1.
1.2.
Меньшая посылка истинна на схеме:
2.1.
Совмещаем схемы:
1.2.+2.1.
1.1.+2.1.
Силлогизм правильный. Энтимема силлогизма –суждения, в кот. 1 из посылок или заключение (или 1 посылка и заключение) опускаются.
Для проверки правильности энтимемы нужно попытаться восстановить пропущенную часть таким образом, чтобы получился правильный силлогизм. Если этого сделать нельзя, то энтимема является неправильной, если удается, то правильной.
При исследовании энтимемы в процессе аргументации целесообразно попытаться установить, является ли восстановленная посылка силлогизма истинной или ложной. Если она оказывается истинной, то аргументация корректная, если нет — некорректная.
Напр., «Дельфины – не рыбы, т.к. они киты». 1. Выделяем заключение (перед словами – «т.к.») – «Дельфины (S) – не рыбы (P) » 2. Выделяем в заключении больший и меньший термины и определяем какой посылкой является – «Дельфины - киты»: · «Дельфины» – меньший термин (S) · «Дельфины - киты» - меньшая посылка
……………………………………. Дельфины (S) суть киты (М) Дельфины (S) не суть рыбы (Р) Итог:
Ни один кит (М) не суть рыбы (Р) Дельфины (S) суть киты (М) Дельфины (S) не суть рыбы (Р)
Фигура:
Правила 1-ой фигуры соблюдены. Соблюдены также общие правила силлогизма. Силлогизм является правильным.
Метод останков. Слож. явление U распадается на ряд простых явлений а, b, с, d. Из предшествующего опыта известно, что простое явление а вызывается обстоятельством А, простое явление b вызывается обстоятельством В, простое явление с — обстоятельством С. Известно, что оставшееся простое явление d не вызвано обстоятельствами А, В, С. Делается вывод, что должно быть какое-то обстоятельство D, которое вызывает явление d. Иногда устанавливается, что явления а, b, с вызваны, соответственно, обстоятельствами А, В, С и есть обстоятельство D. Делается предположение, что оно-то и является причиной явления d.
|

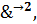
 (…, а затем…; …, а затем…, а затем…) и т.д. в зависимости от числа суждений, из кот. они образуются (напр., Были приглашены понятые, а затем составлен протокол).
(…, а затем…; …, а затем…, а затем…) и т.д. в зависимости от числа суждений, из кот. они образуются (напр., Были приглашены понятые, а затем составлен протокол). B – форма последовательно-конъюнктивного суждения.
B – форма последовательно-конъюнктивного суждения. ) – суждения, в кот. выражается одновременное существование/возникновение 2 ситуаций (напр., Производится выемка документов и присутствуют понятые).
) – суждения, в кот. выражается одновременное существование/возникновение 2 ситуаций (напр., Производится выемка документов и присутствуют понятые). (
( ) – знак n-местной строгой дизъюнкции, где n > 2 (напр., 3-местная: или А, или В, или С).
) – знак n-местной строгой дизъюнкции, где n > 2 (напр., 3-местная: или А, или В, или С). - …, а затем…) отрицается по схеме:
- …, а затем…) отрицается по схеме: B) ↔ ØA v ØB v (A
B) ↔ ØA v ØB v (A  B) v (B
B) v (B 


