
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обобщающая индукция: статистическая и нестатистическаяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Индуктивные умозаключения - такие связи между посылками и заключением по лог. формам, при кот. посылки лишь подтверждают заключение. Отношение подтверждения – «||=». Выражение «Г ||= В» - множество высказываний Г подтверждает высказывание В (из Г индуктивно следует В). Если высказывания Г истинны, то степень правдоподобия В при наличии Г выше, чем при отсутствии Г.
Платон понимал под индукцией обратную дедукцию – если А → В, то В ||= А (если из А следует В, то В подтверждает А).
Аристотель понимал под индукцией обобщающую индукцию – переход от знания о нек. предметах класса к знанию о всех предметах класса.
Обобщающая индукция — умозаключение, в кот. осуществляется переход от знания об отдельных предметах класса или о подклассе класса к знанию о всех предметах класса или о классе в целом: 1. Статистическая - перенос относительной частоты появления признака с нек. класса на более широкий класс
В случае статистической индукции исследуются случайные массовые явления, кот. состоят из событий. Появление конкретного события не предсказуемо, но предсказуема частота появления событий того или иного типа, то есть, как говорят, предсказуемы нек. числовые пропорции целого.
Дождь. Дождь можно рассматривать как явление, состоящее из большого числа событий — выпадения дождевых капель. В последовательности выпадения дождевых капель нет никакой закономерности, но при длительном наблюдении все же можно установить, что на оба камня выпадает одинаковое число капель. Таким образом, дождь — случайное массовое явление, кот. предсказуемо в числовых пропорциях целого, но непредсказуемо в отдельных событиях.
При большом числе наблюдений относительная частота событий А - f (А) во многих случаях оказывается неизменяемым числом - устойчивой относительной частотой или (апостериорной) вероятностью события. Нередко относительная частота нек. события устанавливается путём исследования всех событий, составляющих изучаемое явление.
Статистическая индукция применяется, когда: · Исследуемые классы понятий бесконечны · «Сплошное» исследование связано с большими затратами/практически невозможно · Требуется предсказать события, кот. ещё не наступили
Схема статистической неполной индукции:
Предметы класса S обладают свойством А с относительной частотой f (A). Класс S включается в класс К Предметы класса К обладают свойством А с относительной частотой f (A)
Заключение, получаемое посредством статистической индукции, может оказаться ложным. Научная статистическая индукция (в отличие от ненаучной) для повышения степени правдоподобия заключения использует спец. методологию.
Методологические требования, соблюдение кот. необходимо при применении статистической индукции: · Статистическую индукцию правомерно применять при исследовании предметов, объединенных в одно целое по общим признакам, целям и т.д. Пусть, например, исследованию подлежат психические особенности людей, совершивших преступления. Обозначим выделенную группу людей буквой К. · Переносимое с подкласса на весь класс свойство должно быть тесно связано со свойствами, по которым выделена группа К. В нашем случае второе требование не соблюдено, поскольку совершение преступления не обязательно связано с психическими особенностями. Следовательно, нужно ограничить группу К, например, взять группу К' — людей, совершивших преступление в состоянии душевного волнения (аффекта). Этот класс называется генеральной совокупностью. · Выбор подкласса класса К' для исследования должен производиться не по переносимому свойству, то есть подкласс S (выборочная совокупность/выборка) следует образовывать не по психическим особенностям людей. · Отбор следует осуществлять так, чтобы представители всех подклассов генеральной совокупности, образованные по признакам, от кот. может зависеть переносимый признак, имели возможность попасть в выборку. Например, должны быть охвачены все возрасты правонарушителей, все категории по образованию, образу жизни и т.д. · При отборе предметов для исследования из образованных подклассов генеральной совокупности следует соблюдать принцип пропорциональности - из большего класса отбирать большее число предметов. · Выделив подклассы, из которых следует производить выборку, и установив соответствующие пропорции, нужно правильно установить число предметов, подвергаемых исследованию. «З-н больших чисел» - закономерности, которым подчиняются случайные массовые явления, могут быть обнаружены лишь при достаточно большом числе наблюдений. · Перенос св-ва с подкласса на весь класс следует осуществлять с осторожностью, т.е. при переносе учитывать возможность ошибок.
2. Нестатистическая: · Полная – умозаключение от знания об отдельных предметах класса к знанию обо всех предметах класса, предполагающее исследование каждого предмета этого класса · Неполная - умозаключение от знания лишь о нек. предметах класса к знанию обо всех предметах класса, предполагающее исследование каждого предмета этого класса Ø Научная (популярная/индукция через простое перечисление): v Индукция через отбор – если исследуемое множество имеется в наличии, рекомендуется выполнять методологические требования v Индукция на основе общего – неполная индукция, при кот. в процессе исследования принадлежности предметам определённого св-ва не используются к/л индивидуальные, отличительные признаки этих предметов Ø Ненаучная (популярная/индукция через простое перечисление) – может использоваться методология здравого смысла – применении принципов: v Исследовать как можно больше предметов v Разнообразить выбор предметов для исследования
Схема нестатистической индукции:
Предмет Предмет . . . Предмет Предметы Все предметы класса К обладают св-вом Р
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1080; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.30 (0.01 с.) |

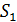 обладает св-вом Р
обладает св-вом Р обладает св-вом Р
обладает св-вом Р обладает св-вом Р
обладает св-вом Р
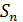 – элементы класса К
– элементы класса К


