
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основвы теории подобия насосов. Формулы подобияСодержание книги
Поиск на нашем сайте
При конструировании новых образцов гидромашинпредворительно проводятся лабораторные испытания модельных конструкцияй. Для перехода от данных полученых на моделях к реальным конструкциям используется теория гидродинамического подобия. Она основана на соблюдении условий геометрического, кинематического и динамического подобия 1) Геометрич подобие: Пропорциональное соотношение натуральной и модельной конструкций:
 2) Кинем подобие: 2) Кинем подобие: 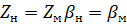 3) Динамич подобие- Равенство чисел Ринольдса в сходственных точках 3) Динамич подобие- Равенство чисел Ринольдса в сходственных точках   Из условия кинематич подобия следует подобие паралелограмма скоростей Из условия кинематич подобия следует подобие паралелограмма скоростей
1. Моделирование подачи QТ=
2. Моделирование напора
3. Моделирование мощности
ℷNг - хар-ет мощность передоваемую насосом жидкости у которой(коэф гидравлической мощности) N=M* ℷМг - коэфгидровлического мом- характеризует мом создоваемый на волу рабочей конструкции Для одного и того же насоса у которого ℷe=1 параметр перещитывается
46. коэффициент быстроходности насоса nsи типы лопастных насосов. в настоящее время широко применяется проектирование пового насоса путем пересчета по формулам подобия размеров существующего насоса. Для того чтобы воспользоваться этим методом, следует выбрать такой насос, у которого режим, подобный заданному режиму работы проектируемого насоса, был бы близок к оптимальному. Для этого необходимо найти параметр, который служил бы критерием подобия и, следовательно, был бы одинаков для всех подобных насосов. Определив по заданным Н,Qип проектируемого насоса этот критерий подобия и сравнив его с критериями подобия имеющихся конструкций, получим возможность подобрать необходимый насос. для подобных насосов, работающих на подобных режимах, справедливы уравнения Коэффициент 3,65 не изменяют физического смысла ns, который, так же как и является критерием (признаком) подобия насосов. Его происхождение историческое. Если насос, геометрически подобный данному, при подаче Q™ 0,075 м3/с имеет напор 1 м, то согласно уравнению (2.47)его коэффициент быстроходности равен частоте вращения насоса. Действительно на этом основании часто коэффициентом быстроходности называют частоту вращения насоса, геометрически подобного данному, которым при напора 1 и подаст0,075 м3/с жидкости.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.168.68 (0.006 с.) |




 → Qn=Qm*ℷ*L3*
→ Qn=Qm*ℷ*L3* 



 →
→ 

 → M=
→ M= 
 ℷMr=
ℷMr= 

 → Q2=
→ Q2= 
 → H2=
→ H2= 
 → N2=
→ N2= 
 Эти уравнений можно записать иначе:
Эти уравнений можно записать иначе:  Величиныqиhодинаковы для подобных насосов, работающих в подобных режимах, и, следовательно, являются критериями подобия. Однако опипе могут быть определены для проектируемого насоса, так как неизвестен его размер L. Для того чтобы исключить из уравненийлинейный размер L, возведем правую и левую части уравнения во вторую степень, а уравнения (2.45) — в третью и разделим уравнения одно на другое:
Величиныqиhодинаковы для подобных насосов, работающих в подобных режимах, и, следовательно, являются критериями подобия. Однако опипе могут быть определены для проектируемого насоса, так как неизвестен его размер L. Для того чтобы исключить из уравненийлинейный размер L, возведем правую и левую части уравнения во вторую степень, а уравнения (2.45) — в третью и разделим уравнения одно на другое: Или
Или  Как параметрыqиh,так иnуодинаковы для геометрически подобных насосов при работе их на подобных режимах независимо от плотности перемещаемой жидкости. Следовательно, параметр nуявляется искомым критерием подобия. Его можно назвать удельной частотой вращения, В насосостроении большее распространение получил параметр ns, называемой коэффициентом быстроходности и в 3,65 раза больший удельной частоты вращения:
Как параметрыqиh,так иnуодинаковы для геометрически подобных насосов при работе их на подобных режимах независимо от плотности перемещаемой жидкости. Следовательно, параметр nуявляется искомым критерием подобия. Его можно назвать удельной частотой вращения, В насосостроении большее распространение получил параметр ns, называемой коэффициентом быстроходности и в 3,65 раза больший удельной частоты вращения: 
 Коэффициент быстроходности различен для разных режимов работы насоса. Назовем коэффициент быстроходности, определенный для оптимального режима, т. е. для режима, соответствующего максимальному значению КПД, коэффициентом быстроходности насоса. Если насосы геометрически подобны, то коэффициент быстроходности у них одинаковы. Следовательно, равенство коэффициентов быстроходности является необходимым признаком подобии насосов. Поскольку на заданные значения параметровп, QоптиНопт и, следовательно, для заданного значения коэффициента (быстроходности можно сконструировать насосы с разными соотношениями размеров, равенство коэффициентов быстроходности не является достаточным признаком геометрического подобия насосов, Однако практикой установлены для каждого коэффициента быстроходности соотношения размеров насоса, обеспечивающие оптимальные технико-экономические показатели. Если ограничиться лишь этими, чаще всего применяющимися в насосах соотношениями размеров, то равенство коэффициентов быстроходности становится не только необходимым, но и в известной степени достаточным признаком (критерием) геометрического подобия насосов. В зависимости от коэффициента быстроходности рабочие колеси лопастных насосов можно разделить на следующие разновидности Центробежное. Центробежные насосы бывают тихоходными и нормальными. Тихоходные пасосы имеют малый коэффициент быстроходности (ns = 50 - 90). Нормальными являются колеса, имеющие ns = 80 - 300. Увеличение быстроходности, связанное с уменьшением напора, ведет к уменьшению выходного диаметра рабочего колеса (D2/D0 — 2,5 -- 1,4). Полуосевые (иа— 250 - 500;D2/D0 = 1,4 -т- 0,9). Осевые, или пропеллерные {п^= 500 ч- 1000; D2/D0 ≈0,8). При дальнейшем увелжченпи быстроходности наклон выходной кромки лопаток возрастает, и она становится почти перпендикулярной к оси насоса. По мере увеличения коэффициента быстроходности кривая напоров Н = f (Q) становится более крутой. Мощность при подаче, равной пулю, увеличивается с ростом быстроходности. Если у насосов с тихоходными и нормальными колесами мощность возрастает с увеличением подачи, то у накосов с полу осевыми колесами она почти не изменяется с изменением подачи, а у насосов с осевыми колесами с увеличением додачи уменьшается. Чем больше коэффициент быстроходности, тем круче падает кривая КПД по обе стороны от оптимального режима и, следовательно, тем меньше становится диапазон подач, в котором работа насоса экономически выгодна. Так как напор лопастного насоса не зависит от рода перекачиваемой жидкости (см. п, 2.6), удельная частота вращенияи коэффициент быстроходности также не зависят от рода жидкости.
Коэффициент быстроходности различен для разных режимов работы насоса. Назовем коэффициент быстроходности, определенный для оптимального режима, т. е. для режима, соответствующего максимальному значению КПД, коэффициентом быстроходности насоса. Если насосы геометрически подобны, то коэффициент быстроходности у них одинаковы. Следовательно, равенство коэффициентов быстроходности является необходимым признаком подобии насосов. Поскольку на заданные значения параметровп, QоптиНопт и, следовательно, для заданного значения коэффициента (быстроходности можно сконструировать насосы с разными соотношениями размеров, равенство коэффициентов быстроходности не является достаточным признаком геометрического подобия насосов, Однако практикой установлены для каждого коэффициента быстроходности соотношения размеров насоса, обеспечивающие оптимальные технико-экономические показатели. Если ограничиться лишь этими, чаще всего применяющимися в насосах соотношениями размеров, то равенство коэффициентов быстроходности становится не только необходимым, но и в известной степени достаточным признаком (критерием) геометрического подобия насосов. В зависимости от коэффициента быстроходности рабочие колеси лопастных насосов можно разделить на следующие разновидности Центробежное. Центробежные насосы бывают тихоходными и нормальными. Тихоходные пасосы имеют малый коэффициент быстроходности (ns = 50 - 90). Нормальными являются колеса, имеющие ns = 80 - 300. Увеличение быстроходности, связанное с уменьшением напора, ведет к уменьшению выходного диаметра рабочего колеса (D2/D0 — 2,5 -- 1,4). Полуосевые (иа— 250 - 500;D2/D0 = 1,4 -т- 0,9). Осевые, или пропеллерные {п^= 500 ч- 1000; D2/D0 ≈0,8). При дальнейшем увелжченпи быстроходности наклон выходной кромки лопаток возрастает, и она становится почти перпендикулярной к оси насоса. По мере увеличения коэффициента быстроходности кривая напоров Н = f (Q) становится более крутой. Мощность при подаче, равной пулю, увеличивается с ростом быстроходности. Если у насосов с тихоходными и нормальными колесами мощность возрастает с увеличением подачи, то у накосов с полу осевыми колесами она почти не изменяется с изменением подачи, а у насосов с осевыми колесами с увеличением додачи уменьшается. Чем больше коэффициент быстроходности, тем круче падает кривая КПД по обе стороны от оптимального режима и, следовательно, тем меньше становится диапазон подач, в котором работа насоса экономически выгодна. Так как напор лопастного насоса не зависит от рода перекачиваемой жидкости (см. п, 2.6), удельная частота вращенияи коэффициент быстроходности также не зависят от рода жидкости.


