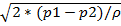Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смоченный периметр, гидравлический радиус. Расход жидкости. Уравнение расхода для элементарной струйки и для потока. Понятие средней скоростиСодержание книги
Поиск на нашем сайте
Смоченный периметр потока – линия, по которой жидкость соприкасается с поверхностями русла в данном живом сечении. Длина этой линии обозначается буквой c. В напорных потоках смоченный периметр совпадает с геометрическим периметром, так как поток жидкости соприкасается со всеми твёрдыми стенками. Гидравлическим радиусом R потока называется часто используемая в гидравлике величина, представляющая собой отношение площади живого сечения S к смоченному периметру c:
Расход потока жидкости (расход жидкости) – количество жидкости, протекающей в единицу времени через живое сечение потока. Различают объёмный, массовый и весовой расходы жидкости.
Расход элементарной струйки – объем жидкости dV, проходящей через живое сечение струйки в единицу времени. Ур-е расхода для струйки и потока: в движении жидкости выделяют отек.элементарные струйки
Средняя скорость потока жидкости Vср в данном сечении это не существующая в действительности скорость потока, одинаковая для всех точек данного живого сечения, с которой должна была бы двигаться жидкость, что бы её расход был равен фактическому. 18. Дифференциальные уравнения движения идеальной жидкости (уравнение Эйлера, вывод) Для вывода уравнения движения жидкости применим основной закон динамики, из которого следует, что равнодействующая всех внешних сил, действующих на данное жидкое тело равна массе тела на ускорение, с которым движется его центр тяжести
x;y;z – ускорение от действ. массовых (объемных) сил;
Результир. ускорение частицы вдоль корд.оси определ. действием вдоль указанной оси массовых и поверхностных сил
Чтобы получить уравнения движения воспользуемся принципом Даламбера для перехода от равновесия к движению необходимо к действующим силам прибавить силы инерции. С учетом того, что уравнение (1) приведено кединицы массы, соответствующие силы инерции будут:
Прибавляя силы инерции, действующие силы к силам получим:
Уравнения (2) были получе6ны в 1755г. Академиком Российской Академии наук Эйлером и названо дифференциальным уравнением движения невязкой жидкости 19.Уравнение Бернулли для элементарной струйки идеальной жидкости (вывод) и его энергетическая и геометрическая интерпретация.
dy dz
W=f(x,y,z):
Геометрическая интерпретация уравнения Бернулли: z – геом. высота, хар-ая положение центра тяж. сеч. относит. произвольно выбр.гориз. пл. сравн. (м)
Энергетическая интерпретация уравнения Бернулли: z – удельная потенциальная энергия положения
20. Уравнение Бернулли для потока вязкой жидкости (вывод). Коэффициент Кориолиса, общие сведения о потерях энергии При выводе уравнения для потока вязкой жидкости считается, что в пределах рассматриваемого сечения справедлив основной закон гидростатики: Мощность потока N - полная энергия, которую проносит поток через данное сечение в единицу времени.
Полная удельная энергия в живом сечении потока E:
Характеризует неравномерное распределение скор.по живому сеч. потока, определяется через отношение действ. кинет. энергии в данном сечении к кинетич. энергии в этом же сечении, но при равномерном распределении скор.
В ур-и для потока в отличии от отур-я для элементарной струйки: 1) кинетич. энергия рассчитывается по средней скор. 2) учитывает неравномерное распределение скор.по сечению потока с помощью коэф. кориолиса α 3) учитывает потери энергии между выбранными сечениями с помощью слагаемого hтр Общие сведения о потерях энергии (напора): При движении реальной жидкости происходит 2 вида потерь энергии: 1.Потери, которые носят систематический характер по всей длине расчётного участка: hДЛ – потери по длине. Они обусловлены гидр.трением между потоком жидкости и стенками трубопровода. 2.Местные потери – возникающие при течении жидкости через местные сопротивления (различные участки потока с изменением скорости по величине или направлению): hМ.
Примеры применения уравнения Бернулли в технике. Расходомер Вентури, скоростная трубка, струйный насос. 1)РасходомерВентури.
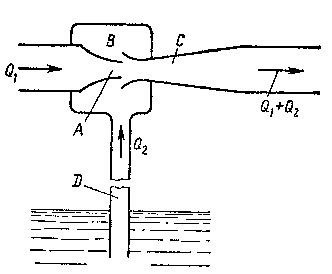
Струйный насос (эжектор) состоит из плавно сходящегося насадка^ А осуществляющего сжатие потока, и постепенно расширяющейся трубки С, установленной на некотором расстоянии от насадка в камере В. Вследствие увеличения скорости потока давление в струе на выходе из насадка и по всей камере В значительно понижается. В расширяющейся трубке скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу), следовательно, в камере В давление обычно меньше атмосферного, т. е. возникает разрежение (вакуум). Под действием разрежения жидкость из нижнего резервуара всасывается по трубе D в камеру В, где происходят слияние и дальнейшее перемешивание двух потоков. Трубка полного напора (или трубка Пито) служит для измерения скорости, например, в трубе. Если установить в этом потоке трубку, изогнутую под углом 90°, отверстием навстречу потоку и пьезометр, то жидкость в этой трубке поднимается над уровнем в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость v частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно, увеличивается на величину скоростного напора. Измерив разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке.На этом же принципе основано измерение скорости полета самолета. На рис. 1.35 показана схема самолетной скоростной трубки (насадка) для измерения малых по сравнению со скоростью звука скоростей полета.Запишем уравнение Бернуллн для струнки, которая набегает натрубку вдоль ее оси, а затем растекается по ее поверхности. Для сечений 0—0 (певоз- мущенный поток) и 1—1 (где v — 0), получаем P0+ρ*v02/2=P1Так как боковые отверстия трубки приближенно воспринимают давление невозмущенного потока, р2 = р0, следовательно из предыдущего имеем Vo≈
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.2.239 (0.007 с.) |







 – ср. скорость
– ср. скорость

 - ускорение от действ.внешних сил
- ускорение от действ.внешних сил (1)
(1)

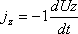
 (2)
(2)




 – инт. Бернулли-Эйлера, характеризует действие на данный выделенный объем движ. жидкости массовых и поверхностных силx = 0; y = 0; z = -g.
– инт. Бернулли-Эйлера, характеризует действие на данный выделенный объем движ. жидкости массовых и поверхностных силx = 0; y = 0; z = -g. – гидродинамич. напор
– гидродинамич. напор – ур. Бернулли для элементарной струйки идеальной жидкости
– ур. Бернулли для элементарной струйки идеальной жидкости – для сжимаемой среды
– для сжимаемой среды - пьезометрическая высота (м)
- пьезометрическая высота (м)  - скоростная высота (м)
- скоростная высота (м) 
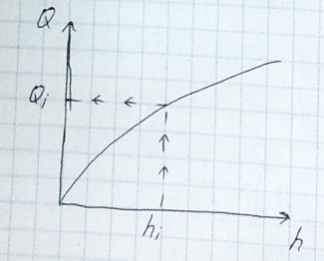
 - полная удельная энергия сечения струйки. При движении идеальной жидкости по длине элем. струйки полная удельная энергия Е сохраняет свое постоянное значение.
- полная удельная энергия сечения струйки. При движении идеальной жидкости по длине элем. струйки полная удельная энергия Е сохраняет свое постоянное значение. Если при переходе из одного сечения к другому происходит увеличение скор, то происх. при этом увеличение кинетич. энергии осуществл. за счет уменьшения на такую же величину удельной потенциальной энергии движения и положения
Если при переходе из одного сечения к другому происходит увеличение скор, то происх. при этом увеличение кинетич. энергии осуществл. за счет уменьшения на такую же величину удельной потенциальной энергии движения и положения , т.е. при движении отдельные струйки оказывают друг на друга в поперечн. направл. такое же давление, как слои жидк, наход. в неподвижн. состоянии.
, т.е. при движении отдельные струйки оказывают друг на друга в поперечн. направл. такое же давление, как слои жидк, наход. в неподвижн. состоянии. , dN – элем.мощн. в живом сечении струйки
, dN – элем.мощн. в живом сечении струйки ;
; 
 ;
; 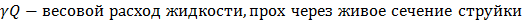


 – ур-е Бернулли для потока вязкой жидкости
– ур-е Бернулли для потока вязкой жидкости - для элементарной струйки идеальной жидкости
- для элементарной струйки идеальной жидкости – коэф. кориолиса
– коэф. кориолиса

 ξдл, ξм – коэф. потерь по длине и местные
ξдл, ξм – коэф. потерь по длине и местные 

 ξдл – зависит от геометрич. размеров трубопровода и режимов движения.ξм – коэф. местных потерь напора, зависит от вида местного сопротивления, а при ламинарном режиме и от скорости движения.
ξдл – зависит от геометрич. размеров трубопровода и режимов движения.ξм – коэф. местных потерь напора, зависит от вида местного сопротивления, а при ламинарном режиме и от скорости движения.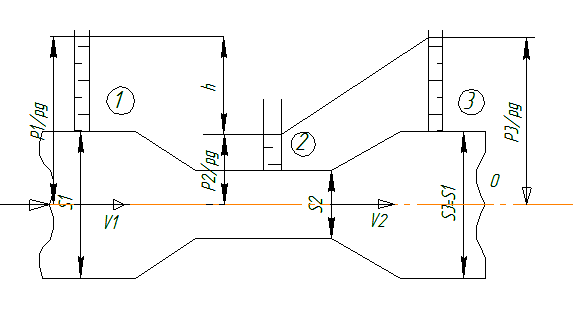
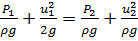 α1=α2=1 т.р.д.
α1=α2=1 т.р.д.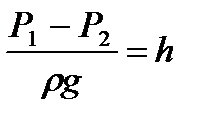
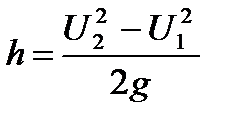
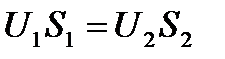 =>
=> 
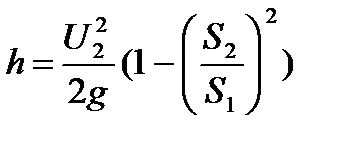
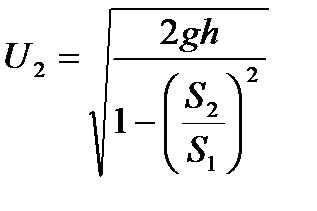
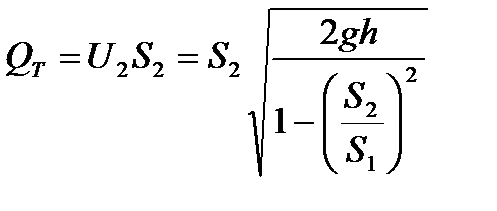 - теорит. расход
- теорит. расход  , где А – константа расх.
, где А – константа расх.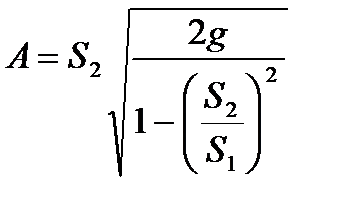
 - действительный расход.
- действительный расход. 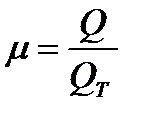 - коэф. расхода – показ., во сколько раз действит. расход меньше теоритического.
- коэф. расхода – показ., во сколько раз действит. расход меньше теоритического.