
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Часть III. Динамический расчет движения автомобиляСодержание книги
Поиск на нашем сайте
Цель работы: освоение студентами основных методов динамического расчета механических систем; определение целесообразных областей использования каждого из этих методов. Основные вопросы, подлежащие разработке: Задачу решить двумя способами: - с помощью теоремы об изменении кинетической энергии механической системы; - с помощью с помощью дифференциальных уравнений движения механической системы. В результате выполнения работы должны быть определены все основные параметры динамики движения автомобиля. Исходные данные: Условие задачи, схема движения автомобиля, значение параметров в таблице 3 согласно заданию.
3.1. Определение динамических характеристик автомобиля с помощью теоремы об изменении кинетической энергии Задание. Какой путь s прошел по прямой до остановки автомобиль, если в момент выключения мотора он двигался со скоростью v =72 км/ч =20 м/с. Вес кузова автомобиля с водителем и пассажирами равен За какое время и на каком расстоянии может быть остановлен тормозом автомобиль, идущий по горизонтальному пути со скоростью v =72 км/ч, если сопротивление движению, развиваемое при торможении, составляет Колеса автомобиля катятся без скольжения. Силой сопротивления воздуха пренебречь (рис. 3.1).
Рисунок 3.1 Решение 1. При движении автомобиля направо направление положительного отсчета угла поворота φ колес выбираем по часовой стрелке. Запишем теорему об изменении кинетической энергии системы материальных точек:
где
Рисунок 3.2 Изобразим внешние силы, приложенные к автомобилю (рис. 3.2):
Сумма работ всех внешних сил системы на искомом перемещении s равна
(коэффициенты «4» соответствуют числу колес автомобиля). Так как разность высот Δ h при перемещениях точек приложения сил
При качении колес без скольжения их мгновенные центры скоростей К находятся в точках касания. Силы трения всегда приложены к колесам в точках, совпадающих с мгновенными центрами скоростей К и перемещаются вместе с ними. Мощность этих сил трения, вычисляемая по формуле
где Следовательно, работа сил трения на конечном перемещении, равная интегралу от мощности по времени, тоже равна нулю:
Учитывая, что радиусы колес и коэффициенты трения качения для всех четырех колес одинаковы, приводим вычисленные суммы работ пар качения к одному колесу, считая нормальное давление равным
Элементарная работа пары трения качения равна
(работа отрицательна, так как направление момента пары трения качения противоположно направлению угла поворота φ колес), где dφ - элементарное угловое перемещение колеса вокруг мгновенного центра скоростей К. Учитывая, что dφ связано с элементарным перемещением ds центра тяжести С колеса зависимостью
получим
Подставляя значение dφ из формулы (3.7) в (3.6), находим:
Для вычисления суммарной работы пары трения качения на конечном перемещении центра тяжести С колеса остается взять от выражения δA по формуле (3.8) определенный интеграл в пределах от 0 до s. После вычислений получим:
Подставляя значения A (P 1), 4 A (P 2), 4 A (Fтр), 4 A (Mтк) из формул (3.4), (3.5) и (3.9) в (3.3), находим сумму работ всех внешних сил, приложенных к автомобилю на его перемещении, равном s:
Переходим к вычислению кинетических энергий автомобиля в его начальном и конечном положениях. Так как в конечном положении, т.е. в момент остановки, скорости всех точек равны нулю, то
Запишем кинетическую энергию
Кузов с водителем и пассажирами совершает поступательно движение, поэтому
Колеса совершают плоское движение, поэтому
так как
то формула (3.14) принимает вид
Внося значения
Подставляя значения
3.2. Определение динамических характеристик движения автомобиля с помощью дифференциальных уравнений
Решение 2. За ось координат примем ось х, направленную вдоль пути торможения автомобиля. Начальными условиями будут:
Интегрируем это уравнение дважды и получаем:
По начальным условиям находим постоянные интегрирования
Тогда
По условию задачи требуется найти время остановки автомобиля, т.е. при v =0 (
Подставляя во второе уравнение движения автомобиля, находим путь пройденный автомобилем до полной остановки:
Таблица 3 – Номера вариантов и исходные данные
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.107 (0.009 с.) |

 =1 кН, вес каждого из четырех колес
=1 кН, вес каждого из четырех колес  = 20 Н. Радиус инерции колеса относительно оси, проходящей через его центр инерции перпендикулярно к плоскости материальной симметрии, равен
= 20 Н. Радиус инерции колеса относительно оси, проходящей через его центр инерции перпендикулярно к плоскости материальной симметрии, равен  = 20 см, радиус колеса r =25 см. Коэффициент трения качения колес о шоссе
= 20 см, радиус колеса r =25 см. Коэффициент трения качения колес о шоссе 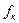 =0.1 см.
=0.1 см.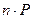 (п – коэффициент пропорциональности, Р - вес автомобиля, С – центр тяжести автомобиля).
(п – коэффициент пропорциональности, Р - вес автомобиля, С – центр тяжести автомобиля).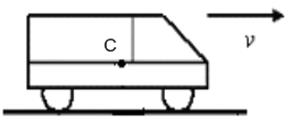
 . (3.1)
. (3.1) - кинетическая энергия автомобиля в первом положении;
- кинетическая энергия автомобиля в первом положении; 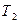 - кинетическая энергия во втором положении автомобиля;
- кинетическая энергия во втором положении автомобиля;  - работа внешних сил, приложенных к автомобилю;
- работа внешних сил, приложенных к автомобилю;  - работа внутренних сил, приложенных к автомобилю.
- работа внутренних сил, приложенных к автомобилю.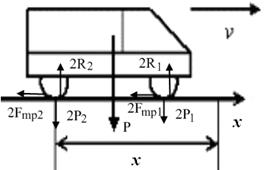
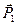 и
и  - силы тяжести колес;
- силы тяжести колес;  и 2
и 2  - нормальные силы реакций, смещенные относительно центра тяжести колес в сторону движения на величину коэффициента трения качения
- нормальные силы реакций, смещенные относительно центра тяжести колес в сторону движения на величину коэффициента трения качения 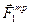 и 2
и 2  – силы трения колес о шоссе, направленные в сторону, противоположную движению (после выключения двигателя все колеса автомобиля оказываются ведомыми). Внутренние силы не изображаем, считая автомобиль неизменяемой системой и пренебрегая силами внутреннего трения. Следовательно, сумма работ всех внутренних сил автомобиля равна нулю. Теперь уравнение (3.1) принимает вид
– силы трения колес о шоссе, направленные в сторону, противоположную движению (после выключения двигателя все колеса автомобиля оказываются ведомыми). Внутренние силы не изображаем, считая автомобиль неизменяемой системой и пренебрегая силами внутреннего трения. Следовательно, сумма работ всех внутренних сил автомобиля равна нулю. Теперь уравнение (3.1) принимает вид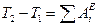 . (3.2)
. (3.2)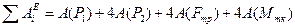 (3.3)
(3.3)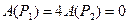 . (3.4)
. (3.4)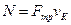
 - скорость мгновенного центра скоростей равна
- скорость мгновенного центра скоростей равна  .
. . (3.5)
. (3.5) . Так как коэффициент трения качения
. Так как коэффициент трения качения 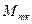 будет
будет .
. (3.6)
(3.6) ,
,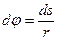 . (3.7)
. (3.7) . (3.8)
. (3.8)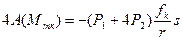 . (3.9)
. (3.9) . (3.10)
. (3.10)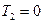 . (3.11)
. (3.11) автомобиля, состоящего из кузова с водителем и пассажирами и четырех колес, в виде
автомобиля, состоящего из кузова с водителем и пассажирами и четырех колес, в виде . (3.12)
. (3.12) . (3.13)
. (3.13)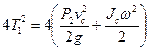 ; (3.14)
; (3.14)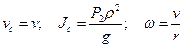 ,
, . (3.15)
. (3.15) и 4
и 4 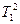 из формул (3.13) и (3.15) в (3.12), находим кинетическую энергию автомобиля в ее начальном положении:
из формул (3.13) и (3.15) в (3.12), находим кинетическую энергию автомобиля в ее начальном положении: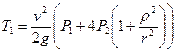 . (3.16)
. (3.16)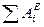 ,
,  и
и 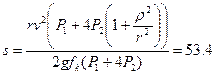 м.
м. ,
, 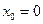 ,
,  . Задаваемые силы – вес автомобиля
. Задаваемые силы – вес автомобиля  и сила сопротивления движению при
и сила сопротивления движению при 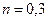 ,
,  . Дифференциальное уравнение движения автомобиля будет иметь вид (рис. 3.2):
. Дифференциальное уравнение движения автомобиля будет иметь вид (рис. 3.2): .
.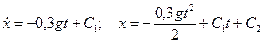 .
. и
и  :
: ,
, .
.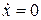 ). Из первого уравнения находим это время:
). Из первого уравнения находим это время: с.
с. м.
м.


