
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Часть II. Расчёт балки на прочность и жёсткостьСодержание книги
Поиск на нашем сайте
Наименование темы: «Расчет балки на прочность и жесткость». Цель работы: освоение студентами основных методов расчета балок (стержней) на прочность и жесткость. Исходные данные: Условие задачи, расчетные схемы балок приведены в приложении Б, значение параметров - в таблице 2 согласно заданию.
Основные расчётные формулы При изгибе стержней в сечениях возникают изгибающие моменты М и поперечные силы Q. Они определяются методом сечений. Величина поперечной силы в произвольном сечении балки равна алгебраической сумме всех внешних поперечных сил, действующих на балку по одну сторону от рассматриваемого сечения. Величина изгибающего момента М в сечении равна алгебраической сумме моментов всех внешних сил по одну сторону от сечения. Между этими внутренними силовыми факторами имеется следующая связь: поперечная сила равна первой производной от изгибающего момента по координате, направленной вдоль оси балки
В свою очередь, между поперечной силой Q и распределённой внешней нагрузкой q имеется аналогичная взаимосвязь
Чтобы изучить работу балки от внешних сил и реакции, необходимо построить эпюры (графики) распределения внутренних силовых факторов – поперечной силы и изгибающего момента по её длине. Сечение, в котором действует наибольший изгибающий момент, называют опасным. В каждой точке балки возникает нормальное напряжение σ, которое линейно изменяется по высоте сечения.
где у - координата слоя балки, в котором определяются напряжения; Iх – осевой момент инерции сечения относительно главной оси. Наибольшее напряжение возникает в нижнем и верхнем слоях сечения
где Прочность балки оценивается по максимальному нормальному напряжению в опасном сечении. Условия прочности балки имеют вид неравенства:
где σП – предельное напряжение материала, из которого изготовлена балка; [ n ] – коэффициент запаса прочности. В сечениях балки возникает касательное напряжение, которое определяется по высоте не линейно (2.6)
где b – ширина слоя сечения;
Касательные напряжения равны нулю в верхнем и нижнем слоях балки и имеют наибольшее значение в слое, проходящем через центр тяжести сечения. Они учитываются при оценке балки на межслойный сдвиг. Касательное напряжение между слоями балки не должны превышать допускаемого
где При изгибе балки её сечения имеют поперечные перемещения у, которые называют прогибами, и угловые перемещения Между прогибом, углом поворота и изгибающим моментом в этом сечении имеются следующие дифференциальные связи:
где E·Iх - параметр, характеризующий жесткость балки на изгиб. Для дифференциальных уравнений (2.8) получены универсальные решения, пригодные для любой балки с прямой осью и постоянной жесткостью:
где а, b, c, d - координаты приложения соответственно сосредоточенного момента m, силы F и распределенной нагрузки q. В практических расчетах часто после расчета на прочность производится проверка выполнения условий жесткости.
где [ у ] и [
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.30 (0.009 с.) |

 . (2.1)
. (2.1) . (2.2)
. (2.2) (2.3)
(2.3) (2.4)
(2.4) - момент сопротивления изгибу относительно оси х.
- момент сопротивления изгибу относительно оси х. (2.5)
(2.5) (2.6)
(2.6) – статический момент площади над слоем.
– статический момент площади над слоем. (2.7)
(2.7) - предельное напряжение (или
- предельное напряжение (или  - предел текучести, или
- предел текучести, или 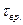 - предел прочности при сдвиге).
- предел прочности при сдвиге). .
.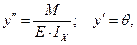 (2.8)
(2.8) (2.9)
(2.9) , (2.10)
, (2.10) и у 0- начальные параметры - угол поворота и прогиб сечения, расположенного в начале координат;
и у 0- начальные параметры - угол поворота и прогиб сечения, расположенного в начале координат; (2.11)
(2.11) ]- допускаемый прогиб и угол поворота сечения, которые устанавливаются на основании опыта эксплуатации аналогичных конструкций.
]- допускаемый прогиб и угол поворота сечения, которые устанавливаются на основании опыта эксплуатации аналогичных конструкций.


