Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила знаков внутренних силовых факторов при построении эпюр сил и моментовСодержание книги
Поиск на нашем сайте
Правила знаков для внутренних усилий, применяемые в машиностроении: 1. Продольная сила 2. Поперечная сила 3. Изгибающий момент положителен, если сжаты верхние волокна отсеченной части, и отрицателен, если сжаты нижние волокна. Эпюра изгибающих моментов строится на сжатых волокнах. 4. Правило знаков для крутящего момента удобно принимать произвольным. 2.2. Методические указания к выполнению задания Задание: Для балки, изображенной на рисунке 2.1, а, построить эпюры поперечных сил и изгибающих моментов. Из расчета на прочность по нормальным напряжениям подобрать номер двутавра. Проверить прочность выбранного двутавра по главным напряжениям, используя третью теорию прочности. Построить изогнутую ось балки. Исходные данные: F =60 кН; M =70 кНм; q =40 кН / м; а =1 м; b =3 м; с =2 м; [ σ ]=155 МПа.
Рисунок 2.1 - Схема балки, эпюр поперечных сил и изгибающих моментов Решение: 1. Определим реакции опор
2. Сделаем проверку:
3. Построение эпюр. Для построения эпюр разобьём балку на три участка и составим уравнение для Q и М. I участок:
При z= 0 При z=a
II участок:
При z=a При z=a+b
III участок:
При z 1 = 0
При z 1 =с
На этом участке график поперечной силы пересекает ось эпюры (рис. 2.1, б). Следовательно, в точке, где
Изгибающий момент при z 1 = 0,85:
По этим данным строим эпюру поперечных сил (рис. 2.1, б) и изгибающих моментов (рис. 2.1, в). 4. Подберём сечение балки. Наибольший изгибающий момент (рисунок 2.1, в) равен 84,45 кН ∙ м. Необходимый момент сопротивления:
По таблицам сортамента (приложение В) ближайшими к этому значению являются Wх= 518 cм 3(двутавр №30а) и Wх= 597 cм 3 (двутавр №33). 5. Проверим, годится ли двутавр №30а. Напряжения в нём будут равны:
То есть перенапряжение составляет:
что допустимо.
Рисунок 2.2 Схема сечения двутавра.
Таким образом, в соответствии с расчётом по нормальным напряжениям следует принять двутавр №30а. Обратим, однако, внимание на то, что сечении над левой опорой балки действуют одновременно значительный изгибающий момент М =80 кН∙м и большая поперечная (перерезывающая) сила Q =100 кН (рис. 2.1). Поэтому в этом сечении надо сделать проверку по главным напряжениям. 6. Проверим условие прочности по третьей теории прочности. Из таблиц сортамента выпишем для двутавра №30а: Iх= 7780 см 4; h= 300 мм; t = 10,7 мм; d= 6,5 мм. Тогда в точке К сечения (рис. 2.2)
Согласно третьей теории прочности должно выполняться условие:
В нашем случае:
7. Определим перенапряжение в точке К. Перенапряжение составляет:
что недопустимо велико (более 5%). Таким образом, надо использовать двутавр большего размера. Окончательно принимаем двутавр №33.
Таблица 2 - Номера вариантов и исходные данные
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 526; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.102.79 (0.006 с.) |

 считается положительной, если она вызывает растяжение отсеченной части и отрицательной, если вызывает ее сжатие.
считается положительной, если она вызывает растяжение отсеченной части и отрицательной, если вызывает ее сжатие.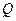 считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицатель ной, если вращение происходит против хода часовой стрелки.
считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицатель ной, если вращение происходит против хода часовой стрелки.
 и
и  , составив для этого условия равновесия:
, составив для этого условия равновесия: ;
;
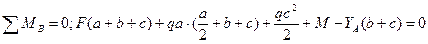 ;
; .
. Реакции найдены правильно.
Реакции найдены правильно.




 .
.


 .
. .
. .
. .
. , изгибающий момент имеет экстремум. Найдём его. Из условия
, изгибающий момент имеет экстремум. Найдём его. Из условия 
 .
.




 .
. .
. .
.