
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесие тела при наличии трения качения.Содержание книги Поиск на нашем сайте
Рассмотрим цилиндр (каток), покоящийся на горизонтальной плоскости, когда на него действует горизонтальная активная сила S;кроме нее, действует сила тяжести Р, а также нормальная реакция N и сила трения Т (рис. 6.10, а). Как показывает опыт, при достаточно малой величине силы S цилиндр остается в покое. Но этот факт нельзя объяснить, если удовлетвориться введением сил, изображенных на рис. 6.10, а. Согласно этой схеме равновесие невозможно, так как главный момент всех сил, действующих на цилиндр Mcz: = — Sr, отличен от нуля и одно из условий равновесия не выполняется.
Этот момент называется моментом трения качения. Составим уравнения равновесия цилиндра: S-T=0, N-P=0, -Sr+Mt=0 (6-12) Первые два, уравнения дают T=S, N = P, а из третьего уравнения можно найти МТ. Затем из (6.11) определяем расстояние между точками С и С1: h=Sr/P (6.13) Как видно, с увеличением модуля активной силы S растет расстояние h. Но это расстояние связано с площадью поверхности контакта и, следовательно, не может неограниченно увеличиваться. Это значит, что наступит такое состояние, когда увеличение силы S приведет к нарушению равновесия. Обозначим максимально возможную величину h буквой δ (см. рис. 6.10, б). Экспериментально установлено, что величина δ пропорциональна радиусу цилиндра и различна для разных материалов. Следовательно, если имеет место равновесие, то выполняется условие h≤δ (6.14) Величина δ называется коэффициентом трения качения; она имеет размерность длины. Условие (6.14) можно также записать в виде Mт≤δN(6.15) или, учитывая (6.12), S ≤δN/r (6.15) Очевидно, что максимальный момент трения качения Mтmax = 8N пропорционален силе нормального давления. В справочных таблицах приводится отношение коэффициента трения качения к радиусу цилиндра (К = 8/г) для различных материалов Чистый сдвиг
При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. d — абсолютный сдвиг, g» δ/а — относительный сдвиг или угол сдвига. Закон Гука при сдвиге:γ=τ/G или τ=Gγ. G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге.G=E/2(1+µ) (Е — модуль упругости, m— коэффициент Пуассона). Потенциальная энергия при сдвиге: U=δQ/V=Q2a/2GF. Удельная потенциальная энергия деформации при сдвиге: u=U/V=Q2a/2GFaF,где V=а×F — объем элемента. Учитывая закон Гука, u=τ2/2G. Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю. напряженность τ=P/ℓδ τ =Mвн/2πR2δ σα= τ ABsinα+ τ BCcosα σ τ α= τ ABcosα- τ BCsinα AB=AC cos α, BC=AC sin α. Отсюда следует, что: σα= τ sin2α τ α= τ cos2α
15. Центртяжести твердого тела – точка, неизменно связанная с этим телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела при любом положении тела в пространстве. При этом поле тяжести считается однородным, т.е. силы тяжести частиц тела параллельны друг другу и сохраняют постоянную величину при любых поворотах тела. Координаты центра тяжести:
Статический момент площади плоской фигуры – сумма произведений элементарных площадей, входящих в состав площади фигуры, на алгебраические значения расстояний до некоторой оси. Sx=åyi×DFi= F×yc; Sy=åxi×DFi= F×xc. Вспомогательные теоремы для определения положения центра тяжести: Т.1. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Т.2. Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости. Т.3. Объем тела вращения, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описанной ее центром тяжести, V=2pxcF.
Определяя положение центра тяжести плоской фигуры с вырезанной из нее частью, можно считать площадь этой части отрицательной и тогда: 24.Теорема о сложении скоростей:
25.Теорема о сложении ускорений (теорема Кориолиса):
3) 4) получаем:
23.Мгновенный центр ускорений – точка (Q) плоской фигуры, ускорение которой в данный момент времени равно нулю. Для его построения из точки А откладываем под углом 20.Движение твердого тела. При сложении двух поступательных движений результирующее движение также является поступательным и скорость результирующего движения равна сумме скоростей составляющих движений. Сложение вращений тв. тела вокруг пересекающихся осей. Ось вращения, положение которой в пространстве изменяется со временем назыв. мгновенной осью вращения тела. Вектор угловой скорости – скользящий вектор, направленный вдоль мгновенной оси вращения. Абсолютная угловая скорость тела = геометрической сумме скоростей составляющих вращений – правило параллелограмма угловых скоростей.
27.Теорема об изменении количества движения матер. точки. 28. Теорема об изменении момента количества движения матер. точки.
29.Работа силы. Мощность. Элементарная работа dA = Ftds, Ft – проекция силы на касательную к траектории, направленная в сторону перемещения, или dA = Fdscosa. Если a – острый, то dA>0, тупой – <0, a=90o: dA=0. dA=
Теорема о работе силы: Работа равнодействующей силы равна алгебраической сумме работ составляющих сил на том же перемещении А=А1+А2+…+Аn. Работа силы тяжести: Работа силы упругости: Работа силы трения: если сила трения const, то Работа силы тяготения. Сила притяжения (тяготения): Мощность – величина, определяющая работу в единицу времени, = 1000 Вт, 1л.с.(лошадиная сила) = 75 кгс×м/с = 736 Вт].
30.Теорема об изменении кинетической энергии точки. В диффер-ной форме: Силовое поле – область, в каждой точке которой на помещенную в ней матер.точку действует сила, однозначно определенная по величине и направлению в любой момент времени, т.е. должно быть известна 1) Работа сил стац. поля зависит в общем случае от начального М1 и конечного М2 положений и траектории, но не зависит от закона движения матер. точки. 2) Имеет место равенство А2,1= – А1,2. Для нестационарных полей эти свойства на выполняются. Примеры: поле силы тяжести, электростатическое поле, поле силы упругости. Стационарные силовые поля, работа сил которых не зависит от траектории (пути) движения матер. точки и определяется только ее начальным и конечным положениями назыв. потенциальными (консервативными).
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.1.38 (0.014 с.) |

 Причина выявившегося несоответствия состоит в том, что в наших рассуждениях мы продолжаем пользоваться представлением об абсолютно твердом теле и предполагаем касание цилиндра с поверхностью происходящим по образующей. Для устранения отмеченного несоответствия теории с опытом необходимо отказаться от гипотезы абсолютно твердого тела и учесть, что в действительности цилиндр и плоскость вблизи точки С деформируются и существует некоторая площадь соприкосновения конечной ширины. Вследствие этого в ее правой части цилинлр прижимается сильнее, чем в левой, и полная реакция R приложена правее точки С (см. точку С1 на рис. 6.10, б). Полученная теперь схема действующих сил статически удовлетворительна, так как момент пары (S, Т) может уравновеситься моментом пары (N, Р). Считая деформацию малой, заменим эту систему сил системой, изображенной на рис. 6.7, в. В отличие от первой схемы (рис. 6.10, а), к цилиндру приложена пара сил с моментом Мт=Nh (6.11)
Причина выявившегося несоответствия состоит в том, что в наших рассуждениях мы продолжаем пользоваться представлением об абсолютно твердом теле и предполагаем касание цилиндра с поверхностью происходящим по образующей. Для устранения отмеченного несоответствия теории с опытом необходимо отказаться от гипотезы абсолютно твердого тела и учесть, что в действительности цилиндр и плоскость вблизи точки С деформируются и существует некоторая площадь соприкосновения конечной ширины. Вследствие этого в ее правой части цилинлр прижимается сильнее, чем в левой, и полная реакция R приложена правее точки С (см. точку С1 на рис. 6.10, б). Полученная теперь схема действующих сил статически удовлетворительна, так как момент пары (S, Т) может уравновеситься моментом пары (N, Р). Считая деформацию малой, заменим эту систему сил системой, изображенной на рис. 6.7, в. В отличие от первой схемы (рис. 6.10, а), к цилиндру приложена пара сил с моментом Мт=Nh (6.11)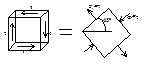 Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения τ=Q/F, где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: σ1=-σ3 σ2=0 Главные площадки составляют с площадками чистого сдвига угол 45о.
Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения τ=Q/F, где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: σ1=-σ3 σ2=0 Главные площадки составляют с площадками чистого сдвига угол 45о. ;
; 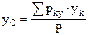 ;
;  , где Р=åрk, xk,yk,zk – координаты точек приложения сил тяжести рk. Центр тяжести – геометрическая точка и может лежать и вне пределов тела (например, кольцо). Центр тяжести плоской фигуры:
, где Р=åрk, xk,yk,zk – координаты точек приложения сил тяжести рk. Центр тяжести – геометрическая точка и может лежать и вне пределов тела (например, кольцо). Центр тяжести плоской фигуры:
 , DFk – элементарная площадка, F – площадь фигуры. Если площадь нельзя разбить на несколько конечных частей, то
, DFk – элементарная площадка, F – площадь фигуры. Если площадь нельзя разбить на несколько конечных частей, то 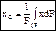 . Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Центр тяжести: дуги окружности с центральным углом 2a:
. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. Центр тяжести: дуги окружности с центральным углом 2a: 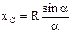 ; кругового сектора:
; кругового сектора: 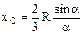 ; треугольник: в точке пересеч. медиан (1/3 медианы от основания).
; треугольник: в точке пересеч. медиан (1/3 медианы от основания). Т.4. Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но не пересекающей ее, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести, F=2pxcL.
Т.4. Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но не пересекающей ее, равна произведению длины этой кривой на длину окружности, описанной ее центром тяжести, F=2pxcL.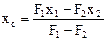 и т.д. — способ отрицательных площадей (объемов).
и т.д. — способ отрицательных площадей (объемов).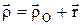 ,
, 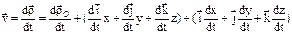 ; рчастныепоэтому скорость его конца
; рчастныепоэтому скорость его конца  и т.д., Þ:
и т.д., Þ:  ,
, ;
;  – относительная скорость.
– относительная скорость. ; переносная скорость:
; переносная скорость:  , поэтому абсолютная скорость точки = геометрической сумме ее переносной (ve) и относительной (vr) скоростей
, поэтому абсолютная скорость точки = геометрической сумме ее переносной (ve) и относительной (vr) скоростей  , модуль:
, модуль:  .
.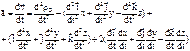
 и т.д. Слагаемые выражения, определяющего ускорения
и т.д. Слагаемые выражения, определяющего ускорения  : 1)
: 1) 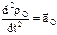 – ускорение полюса О;
– ускорение полюса О;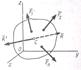
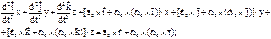
 – относительное ускорение точки;
– относительное ускорение точки;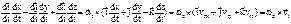 ,
,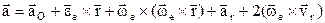 .
. Первые три слагаемых представляют собой ускорение точки в переносном движении:
Первые три слагаемых представляют собой ускорение точки в переносном движении: 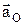 – ускорение полюса О;
– ускорение полюса О;  – вращательное уск.,
– вращательное уск.,  – осестремительное уск., т.е.
– осестремительное уск., т.е. 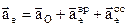 .
.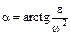 к ускорению аА отрезок
к ускорению аА отрезок  , при этом угол откладывается от ускорения в сторону, направления углового ускорения e. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгн.ц. ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки и м.ц.у. один и тот же угол
, при этом угол откладывается от ускорения в сторону, направления углового ускорения e. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгн.ц. ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки и м.ц.у. один и тот же угол  :
: 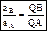 . Мгновенный центр скоростей Р и мгновенный центр ускорений Q являются различными точками плоской фигуры.
. Мгновенный центр скоростей Р и мгновенный центр ускорений Q являются различными точками плоской фигуры.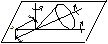
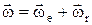 . Если тело участвует одновременно в мгновенных вращениях вокруг нескольких осей, пересекающихся в одной точке, то
. Если тело участвует одновременно в мгновенных вращениях вокруг нескольких осей, пересекающихся в одной точке, то
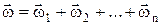 . При сферическом движении твердого тела, одна из точек которого во все время движения остается неподвижной, имеем уравнения сферического движения: Y=f1(t); q=f2(t); j=f3(t). Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Угловая скорость прецессии
. При сферическом движении твердого тела, одна из точек которого во все время движения остается неподвижной, имеем уравнения сферического движения: Y=f1(t); q=f2(t); j=f3(t). Y – угол прецессии, q – угол нутации, j – угол собственного вращения — углы Эйлера. Угловая скорость прецессии 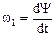 , угл. скорость нутации
, угл. скорость нутации 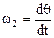 , угл. ск. собственного вращения
, угл. ск. собственного вращения 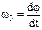 .
.  ,
, – модуль угловой скорости тела вокруг мгновенной оси. Через проекции на неподвижные оси координат:
– модуль угловой скорости тела вокруг мгновенной оси. Через проекции на неподвижные оси координат: 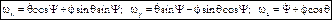 – кинематические уравнения Эйлера.
– кинематические уравнения Эйлера.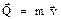 – количество движения материальной точки,
– количество движения материальной точки,  – элементарный импульс силы.
– элементарный импульс силы. 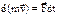 – элементарное изменение количества движения материальной точки равно элементарному импульсу силы, приложенной к этой точке (теорема в дифференц-ной форме) или
– элементарное изменение количества движения материальной точки равно элементарному импульсу силы, приложенной к этой точке (теорема в дифференц-ной форме) или  – производная по времени от количества движения материальной точки равна равнодействующей сил, приложенных к этой точке. Проинтегрируем:
– производная по времени от количества движения материальной точки равна равнодействующей сил, приложенных к этой точке. Проинтегрируем:  – изменение количества движения материальной точки за конечный промежуток времени равно элементарному импульсу силы, приложенной к этой точке, за тот же промежуток времени.
– изменение количества движения материальной точки за конечный промежуток времени равно элементарному импульсу силы, приложенной к этой точке, за тот же промежуток времени. 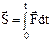 – импульс силы за промежуток времени [0,t]. В проекциях на оси координат:
– импульс силы за промежуток времени [0,t]. В проекциях на оси координат: 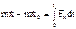 и т.д.
и т.д.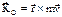 - момент количества движения матер. точки относительно центра О.
- момент количества движения матер. точки относительно центра О. 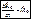 – производная по времени от момента количества движения матер. точки относительно какого-либо центра равна моменту силы, приложенной к точке, относительно того же центра. Проектируя векторное равенство на оси координат. получаем три скалярных уравнения:
– производная по времени от момента количества движения матер. точки относительно какого-либо центра равна моменту силы, приложенной к точке, относительно того же центра. Проектируя векторное равенство на оси координат. получаем три скалярных уравнения: 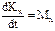 и т.д. - производная от момента кол-ва движения матер. точки относительно какой-либо оси равна моменту силы, приложенной к точке, относительно той же оси. При действии центральной силы, проходящей через О, МО= 0, Þ
и т.д. - производная от момента кол-ва движения матер. точки относительно какой-либо оси равна моменту силы, приложенной к точке, относительно той же оси. При действии центральной силы, проходящей через О, МО= 0, Þ  =const.
=const.  =const, где
=const, где 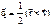 – секторная скорость. Под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью, т.е. радиус-вектор точки описывает ("ометает") равные площади в любые равные промежутки времени (закон площадей) Этот закон имеет место при движении планет и спутников – один из законов Кеплера.
– секторная скорость. Под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью, т.е. радиус-вектор точки описывает ("ометает") равные площади в любые равные промежутки времени (закон площадей) Этот закон имеет место при движении планет и спутников – один из законов Кеплера. – скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= Fxdx+Fydy+Fzdz – аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М0М1:
– скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= Fxdx+Fydy+Fzdz – аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М0М1: 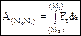 . Если сила постоянна, то
. Если сила постоянна, то  = F×s×cosa. Единицы работы:[1 Дж (джоуль) = 1 Нм].
= F×s×cosa. Единицы работы:[1 Дж (джоуль) = 1 Нм].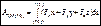 , т.к. dx=
, т.к. dx=  dt и т.д., то
dt и т.д., то 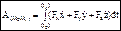 .
. , >0, если начальная точка выше конечной.
, >0, если начальная точка выше конечной.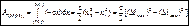 –работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.
–работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.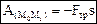 - всегда отрицательна, Fтр=fN, f – коэфф.трения, N – нормальная реакция поверхности.
- всегда отрицательна, Fтр=fN, f – коэфф.трения, N – нормальная реакция поверхности.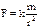 , из mg=
, из mg= 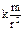 , находим коэфф. k=gR2.
, находим коэфф. k=gR2. 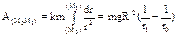 – не зависит от траектории.
– не зависит от траектории.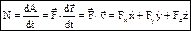 . Если изменение работы происходит равномерно, то мощность постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) =
. Если изменение работы происходит равномерно, то мощность постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) =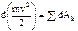 – полный дифференциал кинетической энергии мат.точки = элементарной работе всех действующих на точку сил.
– полный дифференциал кинетической энергии мат.точки = элементарной работе всех действующих на точку сил.  – кинетическая энергия матер.точки. В конечном виде:
– кинетическая энергия матер.точки. В конечном виде: 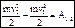 – изменение кинетической энергии мат.точки, при переходе ее из начального в конечное (текущее) положение равно сумме работ на этом перемещении всех сил, приложенных к точке.
– изменение кинетической энергии мат.точки, при переходе ее из начального в конечное (текущее) положение равно сумме работ на этом перемещении всех сил, приложенных к точке.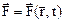 . Нестационарное силовое поле, если
. Нестационарное силовое поле, если  явно зависит от t, стационарное силовое поле, если сила не зависит от времени. Рассматриваются стационарные силовые поля, когда сила зависит только от положения точки:
явно зависит от t, стационарное силовое поле, если сила не зависит от времени. Рассматриваются стационарные силовые поля, когда сила зависит только от положения точки:  и Fx=Fx(x,y,z) и т.д. Свойства стационар. силовых полей:
и Fx=Fx(x,y,z) и т.д. Свойства стационар. силовых полей: , где I и II – любые пути, А1,2 – общее значение работы. В потенциальных силовых полях существует такая функция, однозначно зависящая от координат точек системы, через которую проекции силы на координатные оси в каждой точке поля выражаются так:
, где I и II – любые пути, А1,2 – общее значение работы. В потенциальных силовых полях существует такая функция, однозначно зависящая от координат точек системы, через которую проекции силы на координатные оси в каждой точке поля выражаются так: . Функция U=U(x1,y1,z1,x2,y2,z2,…xn,yn,zn) назыв. силовой функцией. Элементарная работа сил поля: dА=ådАi= dU. Если силовое поле является потенц-ным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции. Работа сил на конечном перемещении
. Функция U=U(x1,y1,z1,x2,y2,z2,…xn,yn,zn) назыв. силовой функцией. Элементарная работа сил поля: dА=ådАi= dU. Если силовое поле является потенц-ным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции. Работа сил на конечном перемещении 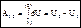 , т.е. работа сил в потенц-ном поле равна разности значений силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом перемещении работа равна 0. Потенциальная энергия П равна сумме работ сил потенциального поля на перемещении системы из данного положения в нулевое. В нулевом положении П0= 0. П=П(x1,y1,z1,x2,y2,z2,…xn,yn,zn). Работа сил поля на перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий А1,2= П1– П2. Эквипотенциальные поверхности – поверхности равного потенциала. Сила направлена по нормали к эквипотенциальной поверхности. Потенциальная энергия системы отличается от силовой функции, взятой со знаком минус, на постоянную величину U0: А1,0= П =U0 – U. Потенциальная энергия поля силы тяжести: П= mgz. Потенц.энерг.поля центральных сил. Центральная сила – сила, которая в любой точке пространства направлена по прямой, проходящей через некоторую точку (центр), и модуль ее зависит только от расстояния r точки массой m до центра:
, т.е. работа сил в потенц-ном поле равна разности значений силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом перемещении работа равна 0. Потенциальная энергия П равна сумме работ сил потенциального поля на перемещении системы из данного положения в нулевое. В нулевом положении П0= 0. П=П(x1,y1,z1,x2,y2,z2,…xn,yn,zn). Работа сил поля на перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий А1,2= П1– П2. Эквипотенциальные поверхности – поверхности равного потенциала. Сила направлена по нормали к эквипотенциальной поверхности. Потенциальная энергия системы отличается от силовой функции, взятой со знаком минус, на постоянную величину U0: А1,0= П =U0 – U. Потенциальная энергия поля силы тяжести: П= mgz. Потенц.энерг.поля центральных сил. Центральная сила – сила, которая в любой точке пространства направлена по прямой, проходящей через некоторую точку (центр), и модуль ее зависит только от расстояния r точки массой m до центра: 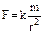 ,
,  . Центральной является гравитационная сила
. Центральной является гравитационная сила 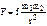 ,
,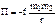 , f = 6,67×10-11м3/(кгс2) – постоянная тяготения. Первая космическая скорость v1=
, f = 6,67×10-11м3/(кгс2) – постоянная тяготения. Первая космическая скорость v1=  » 7,9 км/с, R = 6,37×106м – радиус Земли; тело выходит на круговую орбиту. Вторая космическая скорость: v11=
» 7,9 км/с, R = 6,37×106м – радиус Земли; тело выходит на круговую орбиту. Вторая космическая скорость: v11=  » 11,2 км/с, траектория тела парабола, при v >v11– гипербола. Потенц. энергия восстанавливающей силы пружин:
» 11,2 км/с, траектория тела парабола, при v >v11– гипербола. Потенц. энергия восстанавливающей силы пружин: , l – модуль приращения длины пружины. Работа восстанавливающей силы пружины:
, l – модуль приращения длины пружины. Работа восстанавливающей силы пружины:  , l1 и l2 – деформации, соответствующие начальной и конечной точкам пути.
, l1 и l2 – деформации, соответствующие начальной и конечной точкам пути.


