
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ускорение материальной точкиСодержание книги Поиск на нашем сайте
Можно сказать, что ускоpение точки pавно пpиpащению ее скоpости за одну секунду. Как и скоpость, ускоpение - вектоpная величина. В данном случае ноpмальное ускоpение пpедставляет собой следующий пpедел: Остается выяснить, что собой пpедставляет пpоизводная d /dt. Непосpедственно из pисунка видно, что и 16.Способы задания движения точки Задать движение точки означает задать ее положение в каждый момент времени. Положение это должно определяться, как уже отмечалось, в какой-либо системе координат. Однако для этого не обязательно всегда задавать сами координаты; можно использовать величины, так или иначе с ними связанные. Ниже описаны три основных способа задания движения точки. 1. Естественный способ. r (t) = x(t) i +y(t) j +z(t) k. (1) Преимущество векторной формы записи перед координатной в компактности (вместо трех величин оперируют с одной) и часто в большей наглядности. Для решения первой части задачи воспользуемся координатным способом, направив ось х декартовой системы вдоль стержня и выбрав ее начало в точке А. Поскольку вписанный АМС прямой (как опирающийся на диаметр),
где R радиус полуокружности. Полученный закон движения называется гармоническим колебанием (колебание это будет продолжаться, очевидно, лишь до того момента, пока колечко не дойдет до точки А). Вторую часть задачи будем решать, используя естественный способ. Выберем положительное направление отсчета расстояния вдоль траектории (полуокружности АС) против часовой стрелки (рис. 3), а нуль совпадающим с точкой С. Тогда длина дуги СМ как функция времени даст закон движения точки МS(t) = R2 = 2R t, т.е. колечко будет равномерно двигаться по окружности радиусом R с угловой скоростью 2. Как явствует из проведенного рассмотрения,нуль отсчета времени в обоих случаях соответствовал моменту, когда колечко находилось в точке С.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


 Скоpость изменения скоpости движения точки называется ускоpением, а точнее, ускоpение есть пеpвая пpоизводная от скоpости точки по вpемени или втоpая пpоизводная от pадиуса-вектора по вpемени:
Скоpость изменения скоpости движения точки называется ускоpением, а точнее, ускоpение есть пеpвая пpоизводная от скоpости точки по вpемени или втоpая пpоизводная от pадиуса-вектора по вpемени:



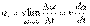
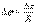

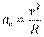
 Этим способом пользуются, если известна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве. При естественном способе необходимо задать (рис. 1):а) траекторию движения (относительно какой-либо системы координат);б) произвольную точку на ней нуль, от которого отсчитывают расстояние S до движущейся частицы вдоль траектории;в) положительное направление отсчета S (при смещении точки М в противоположном направлении S отрицательно);г) начало отсчета времени t; д) функцию S(t), которая называется законом движения**) точки.2. Координатный способ. Это наиболее универсальный и исчерпывающий способ описания движения. Он предполагает задание:а) системы координат (не обязательно декартовой) q1, q2, q3;б) начало отсчета времени t;в) закона движения точки, т.е. функций q1(t), q2(t), q3(t). Говоря о координатах точки, мы всегда будем иметь в виду (если не оговорено противное) ее декартовы координаты.3. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторого начала в данную точку (рис. 2). В этом случае для описания движения необходимо задать:а) начало отсчета радиус-вектора r;б) начало отсчета времени t;в) закон движения точки r (t).Поскольку задание одной векторной величины r эквивалентно заданию трех ее проекций x, y, z на оси координат, от векторного способа легко перейти к координатному. Если ввести единичные векторы i, j, k (i = j = k = 1), направленные соответственно вдоль осей x, y и z (рис. 2), то, очевидно, закон движения может быть представлен в виде*)
Этим способом пользуются, если известна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве. При естественном способе необходимо задать (рис. 1):а) траекторию движения (относительно какой-либо системы координат);б) произвольную точку на ней нуль, от которого отсчитывают расстояние S до движущейся частицы вдоль траектории;в) положительное направление отсчета S (при смещении точки М в противоположном направлении S отрицательно);г) начало отсчета времени t; д) функцию S(t), которая называется законом движения**) точки.2. Координатный способ. Это наиболее универсальный и исчерпывающий способ описания движения. Он предполагает задание:а) системы координат (не обязательно декартовой) q1, q2, q3;б) начало отсчета времени t;в) закона движения точки, т.е. функций q1(t), q2(t), q3(t). Говоря о координатах точки, мы всегда будем иметь в виду (если не оговорено противное) ее декартовы координаты.3. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторого начала в данную точку (рис. 2). В этом случае для описания движения необходимо задать:а) начало отсчета радиус-вектора r;б) начало отсчета времени t;в) закон движения точки r (t).Поскольку задание одной векторной величины r эквивалентно заданию трех ее проекций x, y, z на оси координат, от векторного способа легко перейти к координатному. Если ввести единичные векторы i, j, k (i = j = k = 1), направленные соответственно вдоль осей x, y и z (рис. 2), то, очевидно, закон движения может быть представлен в виде*) Пример. На неподвижную проволочную полуокружность надето маленькое колечко М, через которое проходит еще прямолинейный прут АВ (рис. 3), равномерно вращающийся вокруг точки А (= t, где =const). Найти законы движения колечка М вдоль стержня АВ и относительно полуокружности.
Пример. На неподвижную проволочную полуокружность надето маленькое колечко М, через которое проходит еще прямолинейный прут АВ (рис. 3), равномерно вращающийся вокруг точки А (= t, где =const). Найти законы движения колечка М вдоль стержня АВ и относительно полуокружности. x(t) = AM = 2Rcos = 2Rcost,
x(t) = AM = 2Rcos = 2Rcost,


