
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структура и общие свойства жидкостейСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ЛЕКЦИЯ №5 ЖИДКОСТИ. ЯВЛЕНИЯ ПЕРЕНОСА В ЖИДКОСТЯХ Если в жидкости возникают неоднородности распределения концентрации, температуры или среднеарифметической скорости молекул по объёму, то это порождает явления переноса, подобные наблюдаемым в газах. Законы, описывающие диффузию, теплопередачу и внутреннее трение в жидкостях по форме аналогичны соответствующим законом для газов. Однако коэффициенты переноса отличаются от газовых, как по значениям, так и по своему содержанию. Так в уравнении Фика, которое описывает перенос массы:
коэффициент диффузии для химически однородных жидкостей:
где δ – среднее перемещение молекул, τ0 – средний период колебаний молекул. Коэффициент диффузии быстро возрастает с ростом температуры, главным образом за счёт уменьшения времени релаксации τ. В целом, при температурах Т << Тк значения коэффициента диффузии для жидкостей на 4÷5 порядков меньше, чем для газов при тех же условиях. Например, для воды при Т = 300 К и атмосферном давлении Dж = 1,5∙10-9 м2/с, а для её паров – Dпар = 2∙10-5 м2/с Процесс теплопереноса в жидкостях описывается уравнением Фурье:
В отличие от газов перенос энергии в жидкостях определяется передачей от молекулы к молекуле энергии колебательного, а не поступательного движения. В области повышенной температуры амплитуда колебаний более высокая, чем в соседних областях. Взаимодействие частиц приводит к постепенному возрастанию амплитуд колебаний в областях с более низкой температурой и распространению этого явления по всему объёму жидкости. Коэффициент теплопередачи χ для жидкостей примерно в 100 раз больше, чем для газов. В реальной жидкости между молекулами действуют силы взаимного притяжения, обуславливающие внутреннее трение или вязкость. Это свойство проявляется в том, что при перемещении одних слоев жидкости относительно других, появляются силы, которые препятствуют этому перемещению. В результате, скорость медленно движущихся слоёв возрастает, а быстрых уменьшается. Силы внутреннего трения всегда направлены по касательным к этим слоям. Вязкость вызывает силу сопротивления при перемешивании жидкостей, замедляет скорость движения твёрдых тел в жидкости и т.д.
Сила внутреннего трения между двумя слоями жидкости в случае ламинарного течения определяется законом Ньютона:
Здесь: du/d х – поперечный градиент скорости; S – площадь соприкосновения трущихся слоев; η – динамический коэффициент вязкости или просто вязкость. [η] = Па·с (паскаль∙секунда). Коэффициент вязкости η для жидкостей в 102 ÷ 105 раз больше, чем в газах и при этом сильно зависит от температуры и давления. Например, для воды: при н.у. – А. И. Бачинский экспериментально установил закон зависимости вязкости жидкости от её молярного объёма:
где V – молярный объём жидкости; b – константа в уравнении Ван-дер-Ваальса, С – постоянная, зависящая от природы жидкости. Для большинства жидкостей (вода, низкомолекулярные органи- ческие соединения, истинные растворы, расплавы металлов и их солей) вязкость зависит только от природы жидкости и ее температуры. Такие жидкости называются ньютоновскими. Коэффициент вязкости для них можно рассчитать из формулы (6) или (7). У некоторых жидкостей (кровь, растворы полимеров, суспензии, эмульсии) коэффициент вязкости зависит от режима течения: давления р и значения градиента скорости dυ/d x. При их увеличении вязкость уменьшается вследствие нарушения внутренней структуры потока. Такие жидкости называется структурно вязкими или неньютоновскими. Для них коэффициент вязкости является функцией градиента скорости и давления.
РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ Характер течения жидкости может быть ламинарным (слоистым, равнинная река) или турбулентным (вихревым, горная река). Критерием, по которому определяют, каким будет течение в данном русле, является, так называемое число Рейнольдса:
где ρж – плотность, η – динамическая вязкость, υ – скорость течения жидкости, соответственно; r – характерный размер русла (для круглых труб – радиус). В некоторых случаях (и в формуле Рейнольдса) удобно использовать понятие «кинематическая вязкость»: ν = η / ρж.
Если число Рейнольдса больше некоторого критического значения – Rекр, то движение жидкости будет турбулентным. Например, для гладких цилиндрических труб Rекр= 2300. При Rе < 1000 – течение ламинарное. При 1000 < Rе < 2300 – течение имеет переходной характер. ФОРМУЛА ПУАЗЕЙЛЯ
Выделим в потоке цилиндрический слой длиной l, радиусом r и толщиной dr (рис. 9). Радиус r будем измерять от осевой линии к периферии. Понятно, что слои примыкающие к неподвижным стенкам трубы будут течь медленнее, чем жидкость в середине потока. В силу этого, внутреннее трение, действующее на боковую поверхность выделенного слоя, будет равно:
где S = 2πr l – боковая поверхность цилиндрического слоя, dυ/dr – градиент скорости в области поверхности соприкосновения цилиндра с внешними более медленными слоями жидкости. Знак минус означает, что при возрастании радиуса слоя его скорость уменьшается. Для установившегося течения сила внутреннего трения, действующая на боковую поверхность цилиндра, уравновешивается силами давления, действующими на его основания: Fтр = Fр или
Полагая, что у стенок (на расстоянии R от оси) имеет место полное прилипание жидкости, т.е. скорость равна нулю, получим для выделенного слоя:
Объем жидкости, протекающей через поперечное сечение трубы за 1 с (расход жидкости, объёмная скорость течения) будет определяться соотношением:
Это выражение была установлено эмпирически Гагеном (1839 г.) и Пуазейлем (1840 г.) независимо друг от друга и носит название формулы Пуазейля. Величина
где Δр играет роль напряжения, Q – силы тока, а Z – сопротивления. Из закона Пуазейля следует, что падение давления крови в сосудах (Δр = QZ = 8η l Q/πR4) обратно пропорционально R4. Не случайно, основные фармакологические средства нормализации давления направлены, прежде всего, на изменение просвета сосудов (так, нитроглицерин расслабляет мышцы артериальных стенок). Границы применимости формулы Пуазейля: 1) ламинарное течение; 2) гомогенная жидкость; 3) прямые жесткие трубки; 4) удаление от источников возмущений (изгибов, сужений, входа, выхода и т.д.). Формула Пуазейля (12) лежит в основе многих методов определения вязкости жидкостей.
ПРИМЕНЕНИЕ ПАВ В ФАРМАЦИИ
Используются в производстве мягких лекарственных форм как стабилизаторы и самобилизаторы (растворение в мицеллярных системах нерастворимых в чистых жидкостях соединений называется самобилизацией или коллоидным растворением). ПАВ в медицине должны удовлетворять следующие требования: 1) отсутствие токсичности; 2) стойкость в процессе хранения и от микроорганизма; 3) отсутствие запаха, вкуса и окраски; 4) доступность и возможность получать из отечественного сырья; 5) эффективная стабилизирующая, самобилизирующая, смачивающая и моющая способность.
Анионоактивные ПАВ – соли высших карбоновых кислот (СН = 12÷18) с щелочными металлами (мыла). Служат эмульгаторами I и II рода, самобилизаторами, стабилизаторами мазей и кремов. Эмульсия I рода (прямая) состоит из полярной дисперсионной среды (воды) и неполярной дисперсионной фазы (масло); их обозначают м/в (рис.25а). Эмульсия II рода (обратная) имеет неполярную дисперсионную среду (масло) и полярную дисперсионную фазу (вода); их обозначают в/м (рис.25б). Другие сочетания невозможны. Катионактивные ПАВ – соли алюминиевых, сульфониевых, фосфониевых оснований – используют как бактерицидные, фугицидные и дезинфицирующие средства. Амфотерные ПАВ – алкиламинокислоты, сульфобетаины, в зависимости от РН проявляют свойства анионных (в щелочной среде) или катионных ПАВ (в кислотной среде). Неионогенные ПАВ – твины (эмульгаторы I рода (самобилизаторы гормонов, масел, витаминов, антибиотиков), плюроники (самобилизаторы витаминов, антибиотиков, шампуней, зубных паст)). Широко применяют в фармации маслорастворимые неионогенные ПАВ, образованные на основе одноатомных спиртов алифатического ряда додецилового, тетрадецилового и октидецилового. Они являются эффективными эмульгаторами II рода (в/м). Жиросахара (сложные эфиры сахарозы и одноосновных высших корбоновых кислот). Они не раздражают слизистые, не вызывают жжения глаз, их употребляют в зубных пастах, шампунях, мыле и моющих средствах; некоторые используют для образования кишечнорастворимых покрытий на таблетках с целью защиты их от воздействия желудочного сока. ТВЕРДЫЕ ТЕЛА.
Твердое тело – агрегатное состояние вещества, для которого характерно наличие значительных сил межмолекулярного взаимодействия, стабильность формы и объема. Тепловое движение частиц твердого тела представляет собой небольшие по амплитуде колебания около положений равновесия. Различают кристаллическое и аморфное строение твердых тел.
АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА.
Аморфные твердые тела по многим своим свойствам и главным образом по микроструктуре следует рассматривать как сильно переохлажденные жидкости с очень высоким коэффициентом вязкости. Структура таких тел характеризуется только ближним порядком в расположении частиц. Некоторые из таких веществ вообще не способны кристаллизоваться: воск, сургуч, смолы. Другие при определённом режиме охлаждения образуют кристаллические структуры, но в случае быстрого охлаждения рост вязкость препятствует упорядочению в расположении частиц. Вещество затвердевает раньше, чем реализуется процесс кристаллизации. Такие тела называются стеклообразными: стекло, лёд. Процесс кристаллизации в таком веществе может произойти и после затвердевания (помутнение стёкол). К аморфным относят и твёрдые органические вещества: резина, дерево, кожа, пластмассы, шерстяные, хлопковые и шёлковые волокна. Процесс перехода таких веществ из жидкой фазы в твёрдую представлен на рис. – кривая I.
Аморфные тела не имеют температуры затвердевания (плавления). На графике Т = f(t) имеется точка перегиба, которую называют температурой размягчения. Снижение температуры приводит к постепенному росту вязкости. Такой характер перехода в твёрдое состояние, обуславливает отсутствие у аморфных веществ удельной теплоты плавления. Обратный переход, когда теплота подводится, происходит плавное размягчение до состояния жидкости.
ТВЕРДЫЕ ТЕЛА.
Твердое тело, агрегатное состояние вещества, для которого характерно наличие значительных сил межмолекулярного взаимодействия, стабильность формы и объема. Тепловое движение частиц твердого тела представляет собой небольшие по амплитуде колебания около положений равновесия. Различают кристаллическое и аморфное строение твердых тел. Характерной особенностью микроструктуры кристаллов является пространственная периодичность их внутренних электрических полей и повторяемость в расположении кристаллообразующих частиц – атомов, ионов и молекул (дальний порядок). Частицы чередуются в определенном порядке вдоль прямых линий, которые называются узловыми. В любом плоском сечении кристалла две пересекающихся системы таких линий образуют совокупность совершенно одинаковых параллелограммов, которые плотно, без зазоров покрывают плоскость сечения. В пространстве пересечение трех некомпланарных систем таких линий образует пространственную сетку, которая разбивает кристалл на совокупность совершенно одинаковых параллелепипедов. Точки пересечения линий, образующих кристаллическую решетку называются узлами. Расстояния между узлами вдоль какого-то направления называется трансляциями или периодами решетки. Параллелепипед, построенный на трех некомпланарных трансляциях, называется элементарной ячейкой или параллелепипедом повторяемости решетки. Важнейшим геометрическим свойством кристаллических решеток является симметрия в расположении частиц по отношению к определенным направлениям и плоскостям. По этой причине, хотя и существует несколько способов выбора элементарной ячейки, для данной кристаллической структуры, выбирают ее так, чтобы она соответствовала симметрии решетки. Существует два признака, по которым классифицируются кристаллы: а) кристаллографический – по геометрии кристаллической решетки и б) физический – по характеру взаимодействия частиц, расположенных в узлах кристаллической решетки и их природе.
Геометрия кристаллических решеток и их элементарных ячеек определяется количеством элементов симметрии, использованных при построении данной решетки. Число возможных видов симметрии ограничено. Русский кристаллограф Е.С. Федоров (1853 – 1919) показал, что существует всего 230 возможных комбинаций элементов симметрии, которые путем параллельного переноса, отражения и вращения обеспечивают плотную, т.е. без зазоров и щелей упаковку элементарных ячеек в пространстве. Браве показал, что существует всего 14 типов решеток, которые различаются по виду переносной симметрии. Различают примитивные (простые), базоцентрированные, обьемноцентрированные и гранецентрированные решетки Браве. По форме ячейки в зависимости от углов между ее гранями α, β и γ и соотношением между длиной ребер а, б и с эти 14 типов решеток образуют семь кристаллических систем (сингоний): кубическую, гексогональную, тетрагональную, тригональную или ромбоэдрическую, ромбическую, моноклинную и тригональную. По характеру взаимодействия частиц, расположенных в узлах кристаллической решетки и их природе кристаллы делятся на четыре типа: ионные, атомные, металлические и молекулярные Ионные – в узлах кристаллической решетки располагаются ионы противоположных знаков; взаимодействие обусловлено электростатическими силами притяжения (ионная или гетерополярная связь). Атомные – в узлах кристаллической решетки располагаются нейтральные атомы, удерживающиеся в узлах гомеополярными, или ковалентными связями. Металлические – в узлах кристаллической решетки располагаются положительные ионы металла; свободные электроны образуют, так называемый, электронный газ, который и обеспечивает связь ионов. Молекулярные – в узлах кристаллической решетки располагаются нейтральные молекулы, силы взаимодействия между которыми обусловлены незначительным смещением электронного облака атома (поляризационные или ван-дер-ваальсовские силы). Кристаллические тела можно разделить на две группы: монокристаллы и поликристаллы. Для монокристаллов наблюдается единая кристаллическая решетка в объеме всего тела. И хотя внешняя форма монокристаллов одного вида может быть разной, углы между соответствующими гранями будут всегда одинаковыми. Характерной особенностью монокристаллов является анизотропия механических, тепловых, электрических, оптических и др. свойств. Монокристаллы нередко встречаются в естественном состоянии в природе. Например, большинство минералов – хрусталь, изумруды, рубины. В настоящее время в производственных целях многие монокристаллы выращивают искусственно из растворов и расплавов - рубины, германий, кремний, арсенид галия. Один и тот же химический элемент может образовать несколько, отличающихся по геометрии, кристаллических структур. Это явление получило название - полиморфизма. Например, углерод – графит и алмаз; лед пять модификаций и др. Правильная внешняя огранка и анизотропия свойств, как правило, не проявляются для кристаллических тел. Это объясняется тем, что кристаллические твердые тела обычно состоят из множества беспорядочно ориентированных мелких кристалликов. Такие твердые тела называются поликристаллическими. Связано это с механизмом кристаллизации: при достижении необходимых для этого процесса условий, очаги кристаллизации одновременно возникают во множестве мест исходной фазы. Зародившиеся кристаллы расположены и ориентированы друг по отношению к другу совершенно хаотически. По этой причине по окончании процесса мы получаем твердое тело в виде конгломерата сросшихся мелких кристалликов – кристаллитов. ДЕФФЕКТЫ В КРИСТАЛАХ. Реальные кристаллы обладают рядом нарушений идеальной структуры, которые называются дефектами кристаллов: а) точечные дефекты - дефекты Шотки (незанятые частицами узлы); - дефекты Френкеля (смещение частиц из узлов в междуузлия); - примеси (внедренные чужеродные атомы); б) линейные – дислокации краевые и винтовые локальные нарушения в регулярности расположения частиц, из-за недостроенности отдельных атомных плоскостей, или в последовательности их застройки; в) плоскостные – границы между зеркалами, ряды линейных дислокаций. АМОРФНЫЕ ТВЕРДЫЕ ТЕЛА. Аморфные твердые тела по многим своим свойствам и главным образом по микроструктуре следует рассматривать как сильно переохлажденные жидкости с очень высоким коэффициентом вязкости. С энергетической точки зрения различие между кристаллическими и аморфными твердыми телами хорошо прослеживаются в процессе отвердевания и плавления. Кристаллические тела имеют точку плавления – температуру, когда вещество устойчиво существует в двух фазах – твердой и жидкой (рис1). Переход молекулы твердого тела в жидкость означает, что она приобретает дополнительно три степени свободы поступательного движения. Т.о. единица массы вещества при Тпл. в жидкой фазе имеет большую внутреннюю энергию, чем такая же масса в твердой фазе. Кроме того, меняется расстояние между частицами. Поэтому в целом количество теплоты необходимое для превращения единицы массы кристалла в жидкость будет:
λ = (Uж-Uk) + P (Vж-Vk),
где λ – удельная теплота плавления (кристаллизации), (Uж-Uk) – разность внутренних энергий жидкой и кристаллической фаз, Р – внешнее давление, (Vж-Vk) – разность удельных объемов. Согласно уравнению Клайперона - Клаузиуса температура плавления зависит от давления:
Видно, что если (Vж-Vk)> 0, то У аморфных тел теплота плавления отсутствует. Нагревание приводит к постепенному увеличению скорости теплового движения и уменьшению вязкости. На графике процесса имеется точка перегиба, которую условно называют температурой размягчения.
Фазовые переходы. Диаграммы состояния. Тройная точка. Фазой называется термодинамическое равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Переход вещества из одной фазы в другую – фазовый переход - всегда связан с качественными изменениями свойств тела. Примером фазовых переходов могут служить изменения агрегатного состояния. Но понятие «фазовый переход» шире, т.к. оно включает и переход вещества из одной модификации в другую при сохранении агрегатного состояния (полиморфизм). Пример, превращение алмаза в графит. Различают два вида фазовых переходов. Фазовый переход 1 рода – сопровождается поглощением или выделением теплоты, изменением объема и протекает при постоянной температуре. Примеры: плавление, кристаллизация, испарение, сублимация (возгонка) и др. Фазовые переходы 2 рода – протекают без выделения или поглощения тепла, с сохранением величины объема, но скачкообразным изменением теплоемкости. Примеры: переход ферромагнитных минералов при определенных значениях давления и температуры в парамагнитное состояние (железо, никель); переход некоторых металлов и сплавов при температуре близкой к 00К в сверхпроводящее состояние (ρ = 0 Ом∙м) и др. Для химически однородного вещества понятие фазы совпадает с понятием агрегатное состояние. Рассмотрим для такой системы фазовые превращения, используя для наглядности диаграмму состояния (рис2). На ней в координатах Р и Т задается зависимость между температурами фазовых переходов и давлением. Эти зависимости в виде кривых испарения (ОИ), плавления (ОП) и сублимации (ОС) и образуют диаграмму состояния. Точка О пересечения кривых определяет условия (Т и Р), когда все три агрегатных состояний вещества находятся в термодинамическом равновесии. По этой причине она называется тройной точкой. Например, тройная точка воды является одной из реперных точек (00С) температурной шкалы Цельсия. Как следует из уравнения Клайперона – Клаузиуса характер зависимости Т = f(Р) перехода твердое тело – жидкость для веществ, которые при переходе в жидкую фазу увеличивают объем (вода, германий, чугун), рис.2а, и веществ, для которых характерно уменьшение объема, рис. 2б - разный. Кривая испарения заканчивается критической точкой - К. Как видно из диаграммы, существует возможность непрерывного перехода жидкости в газообразную фазу без пересечения кривой испарения, т.е. без присущих такому переходу фазовых превращений. При давлении меньшим, Р – тройной точки, вещество может существовать только в двух фазах: твердой и газообразной. Причем, при температурах, меньших Ттр.тчк., возможен переход из твердого состояния в газ минуя жидкую фазу. Такой процесс называется сублимацией или возгонкой. Удельная теплота сублимации τсуб = λпл + rисп
ЛЕКЦИЯ №5 ЖИДКОСТИ. СТРУКТУРА И ОБЩИЕ СВОЙСТВА ЖИДКОСТЕЙ
Вещество в зависимости от условий, в которых оно находится, может иметь разные агрегатные состояния: твердое, жидкое, газообразное или состояние плазмы. Главным образом это зависит от температуры Т и давления – р. Значения этих параметров определяет характер взаимодействия между молекулами от чего, в свою очередь, зависит структура и свойства вещества. Жидкости в этом смысле занимают промежуточное положение между газами и твердыми телами. В частности, для жидкости, как и для кристаллических тел, характерно наличие определённого объёма, и вместе с тем жидкость, подобно газу, принимает форму сосуда, в котором находится. Тем не менее жидкость нельзя рассматривать просто как сильно сжатый газ: количественное различие в плотностях настолько велико, что свойства жидкостей во многом значительно отличаются от свойств газов. В первую очередь это относится к различию в характере теплового движения молекул жидкости и газа. Свойства жидкостей их структура, особенности движения молекул представляют особый интерес для биофизиков и медиков, т.к. биоорганизмы больше, чем на половину состоят из жидкостей. Обмен веществ, снабжение клеток кислородом, выведение из организмов продуктов жизнедеятельности обеспечивается именно перемещением жидкостей. Молекулы в жидкостях находятся значительно ближе друг к другу, чем в газах. По этой причине силы межмолекулярного взаимодействия в жидкости значительно больше, чем в газе. Соответственно поправка р´= а/V2 на добавочное давление в уравнении состояния Ван-дер-Ваальса, как показывает расчёт, очень велика: примерно в 106 раз больше, чем в газах. Например, для воды ван-дер-ваальсово давление равно примерно 11 000 атмосфер. Именно этой огромной величиной молекулярного давления объясняется ничтожно малая сжимаемость жидкостей даже при значительном изменении внешнего давления. Структура жидкостей (их молекулярное строение) характерна тем, что расстояние между частицами является неодинаковым и непостоянным. В расположении молекул и атомов наблюдается ближний порядок. Это означает, что ближайшие соседи каждой молекулы по отношению друг к другу имеют определенную ориентацию и расположение. Однако, по мере удаления от «центра наблюдения» расположение частиц становится все менее упорядоченным и уже на расстояниях 3–4-ёх молекулярных диаметров совершенно исчезает (рис.1- Яковлев, стр. 208). Наличие ближнего порядка в расположении молекул жидкости подтверждено данными рентгеноструктурного анализа. В целом это обуславливает изотропию свойств жидкостей. Исключение в этом плане составляют жидкости с удлиненной или дискообразной формой молекул, для которых, при определенных условиях, упорядоченная ориентация частиц наблюдается в пределах значительных объёмов. Такие жидкости получили название жидких кристаллов, т.к. для них, в силу указанной особенности структуры, наблюдается анизотропия механических, оптических, электрических и др. свойств, подобно тому, как это имеет место в кристаллах. Тепловое движение частиц жидкости, по теории Я. И. Френкеля, представляет собой периодические колебания, со средней частотой ν0 ~1012 с-1, которые чередуются с нерегулярными переходами, «скачками», частиц с места на место. При этом частица перемещается на расстояние δ ~ 10-8 – 10-10 м, равное среднему расстоянию между молекулами. Т.к. среднее расстояние между молекулами того же порядка, что и их размеры, то перемещение частиц по объёму жидкости крайне затруднено. Среднее время пребывания молекул на одном месте, время «оседлой жизни» (время релаксации), связано с периодом их колебаний и быстро убывает с ростом температуры:
где Еа – энергия активации: энергия, которую должна приобрести молекула для разрыва молекулярных связей со своими соседями при смене места; k – постоянная Больцмана; В случае несферической формы молекулы жидкости могут совершать кроме колебаний также вращательное и вращательно-колебательное движения. Такая структура жидкостей и характер поведения её молекул обеспечивает сильно выраженную самодиффузию частиц жидкости и её основное свойство – текучесть. Вместе с тем, жидкости практически несжимаемы и сохраняют свой объем подобно твердым телам. Сближает жидкости с твердыми телами и то обстоятельство, что они способны сопротивляться растяжению. По сравнению с газами жидкости обладают значительным коэффициентом теплового расширения. Значения коэффициентов объёмного расширения при постоянном давлении (p = const):
приведены в таблице (Яковлев сттр. 213). Молярные теплоёмкости Ср и СV для жидкостей тоже существенно отличаются от соответствующих значений для их паров. (табл Яковлнев стр. 214) Интересно отметить, что для жидкостей не выполняется уравнение Майера: Ср – СV = R. В тоже время из теории известно, что значения γ = Ср /СV для жидкостей примерно такие же, как и у газов.
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.83.45 (0.018 с.) |

 , (3)
, (3) , (4)
, (4) . (5)
. (5) . (6)
. (6)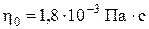 , а при 900 С и атмосферном давлении –
, а при 900 С и атмосферном давлении –  . В целом вязкость жидкости, как установил Я. И. Френкель, пропорциональна времени релаксации (η ~
. В целом вязкость жидкости, как установил Я. И. Френкель, пропорциональна времени релаксации (η ~  ), которое уменьшается с ростом температуры. Т.е. при нагревании жидкостей их текучесть должна возрастать, что подтверждается опытом. Это связано с возрастанием среднего расстояния между молекулами и, следовательно, ослаблением взаимодействия между ними.
), которое уменьшается с ростом температуры. Т.е. при нагревании жидкостей их текучесть должна возрастать, что подтверждается опытом. Это связано с возрастанием среднего расстояния между молекулами и, следовательно, ослаблением взаимодействия между ними. , (7)
, (7) , (8)
, (8) Рассмотрим ламинарное течение вязкой жидкости по трубе радиусом R. Очевидно, что слои жидкости в трубе, будут представлять собой цилиндры, расположенные коаксиально по отношению к геометрической оси трубы. Скорости разных слоев жидкости будут разными и лежат в интервале от нуля (для слоя прилипшего к стенкам трубы) до
Рассмотрим ламинарное течение вязкой жидкости по трубе радиусом R. Очевидно, что слои жидкости в трубе, будут представлять собой цилиндры, расположенные коаксиально по отношению к геометрической оси трубы. Скорости разных слоев жидкости будут разными и лежат в интервале от нуля (для слоя прилипшего к стенкам трубы) до 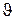 max (для слоя, который движется по оси этой трубы (см. диаграмму распределения скоростей рис.1).
max (для слоя, который движется по оси этой трубы (см. диаграмму распределения скоростей рис.1). , (9)
, (9) , откуда
, откуда 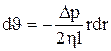 . (10)
. (10) . (11)
. (11) Из (11) видно, что скорости частиц жидкости распределены по параболическому закону, причем вершина параболы лежит на оси трубы (рис.).
Из (11) видно, что скорости частиц жидкости распределены по параболическому закону, причем вершина параболы лежит на оси трубы (рис.). . (12)
. (12) в формуле (10) называется гидравлическим сопротивлением сосуда. По аналогии с законом Ома (12) можно переписать в виде:
в формуле (10) называется гидравлическим сопротивлением сосуда. По аналогии с законом Ома (12) можно переписать в виде: , (13)
, (13)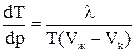 .
. > 0, т.е. с ростом давления температура плавления повышается. Если же объем вещества при плавлении уменьшается (Vж-Vk)< 0 (вода, висмут), то рост давления приводит к понижению Тпл.
> 0, т.е. с ростом давления температура плавления повышается. Если же объем вещества при плавлении уменьшается (Vж-Vk)< 0 (вода, висмут), то рост давления приводит к понижению Тпл. , (1)
, (1)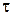 0 – средний период колебаний молекул. Среднее значение скорости поступательного движения молекул жидкости при «скачке»:
0 – средний период колебаний молекул. Среднее значение скорости поступательного движения молекул жидкости при «скачке»:  ~ 40 м/с, что примерно в 20 раз меньшие, чем для газа при той же температуре.
~ 40 м/с, что примерно в 20 раз меньшие, чем для газа при той же температуре. (2)
(2)


