
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Явления переноса в жидкостяхСодержание книги Поиск на нашем сайте Если в жидкости возникают неоднородности распределения концентрации, температуры или среднеарифметической скорости молекул по объёму, то это порождает явления переноса, подобные наблюдаемым в газах. Законы, описывающие диффузию, теплопередачу и внутреннее трение в жидкостях по форме аналогичны соответствующим законом для газов. Однако коэффициенты переноса отличаются от газовых, как по значениям, так и по своему содержанию. Так в уравнении Фика, которое описывает перенос массы:
коэффициент диффузии для химически однородных жидкостей:
где δ – среднее перемещение молекул, τ0 – средний период колебаний молекул. Коэффициент диффузии быстро возрастает с ростом температуры, главным образом за счёт уменьшения времени релаксации τ. В целом, при температурах Т << Тк значения коэффициента диффузии для жидкостей на 4÷5 порядков меньше, чем для газов при тех же условиях. Например, для воды при Т = 300 К и атмосферном давлении Dж = 1,5∙10-9 м2/с, а для её паров – Dпар = 2∙10-5 м2/с Процесс теплопереноса в жидкостях описывается уравнением Фурье:
В отличие от газов перенос энергии в жидкостях определяется передачей от молекулы к молекуле энергии колебательного, а не поступательного движения. В области повышенной температуры амплитуда колебаний более высокая, чем в соседних областях. Взаимодействие частиц приводит к постепенному возрастанию амплитуд колебаний в областях с более низкой температурой и распространению этого явления по всему объёму жидкости. Коэффициент теплопередачи χ для жидкостей примерно в 100 раз больше, чем для газов. В реальной жидкости между молекулами действуют силы взаимного притяжения, обуславливающие внутреннее трение или вязкость. Это свойство проявляется в том, что при перемещении одних слоев жидкости относительно других, появляются силы, которые препятствуют этому перемещению. В результате, скорость медленно движущихся слоёв возрастает, а быстрых уменьшается. Силы внутреннего трения всегда направлены по касательным к этим слоям. Вязкость вызывает силу сопротивления при перемешивании жидкостей, замедляет скорость движения твёрдых тел в жидкости и т.д. Сила внутреннего трения между двумя слоями жидкости в случае ламинарного течения определяется законом Ньютона:
Здесь: du/d х – поперечный градиент скорости; S – площадь соприкосновения трущихся слоев; η – динамический коэффициент вязкости или просто вязкость. [η] = Па·с (паскаль∙секунда). Коэффициент вязкости η для жидкостей в 102 ÷ 105 раз больше, чем в газах и при этом сильно зависит от температуры и давления. Например, для воды: при н.у. – А. И. Бачинский экспериментально установил закон зависимости вязкости жидкости от её молярного объёма:
где V – молярный объём жидкости; b – константа в уравнении Ван-дер-Ваальса, С – постоянная, зависящая от природы жидкости. Для большинства жидкостей (вода, низкомолекулярные органи- ческие соединения, истинные растворы, расплавы металлов и их солей) вязкость зависит только от природы жидкости и ее температуры. Такие жидкости называются ньютоновскими. Коэффициент вязкости для них можно рассчитать из формулы (6) или (7). У некоторых жидкостей (кровь, растворы полимеров, суспензии, эмульсии) коэффициент вязкости зависит от режима течения: давления р и значения градиента скорости dυ/d x. При их увеличении вязкость уменьшается вследствие нарушения внутренней структуры потока. Такие жидкости называется структурно вязкими или неньютоновскими. Для них коэффициент вязкости является функцией градиента скорости и давления.
РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ Характер течения жидкости может быть ламинарным (слоистым, равнинная река) или турбулентным (вихревым, горная река). Критерием, по которому определяют, каким будет течение в данном русле, является, так называемое число Рейнольдса:
где ρж – плотность, η – динамическая вязкость, υ – скорость течения жидкости, соответственно; r – характерный размер русла (для круглых труб – радиус). В некоторых случаях (и в формуле Рейнольдса) удобно использовать понятие «кинематическая вязкость»: ν = η / ρж. Если число Рейнольдса больше некоторого критического значения – Rекр, то движение жидкости будет турбулентным. Например, для гладких цилиндрических труб Rекр= 2300. При Rе < 1000 – течение ламинарное. При 1000 < Rе < 2300 – течение имеет переходной характер. ФОРМУЛА ПУАЗЕЙЛЯ
Выделим в потоке цилиндрический слой длиной l, радиусом r и толщиной dr (рис. 9). Радиус r будем измерять от осевой линии к периферии. Понятно, что слои примыкающие к неподвижным стенкам трубы будут течь медленнее, чем жидкость в середине потока. В силу этого, внутреннее трение, действующее на боковую поверхность выделенного слоя, будет равно:
где S = 2πr l – боковая поверхность цилиндрического слоя, dυ/dr – градиент скорости в области поверхности соприкосновения цилиндра с внешними более медленными слоями жидкости. Знак минус означает, что при возрастании радиуса слоя его скорость уменьшается. Для установившегося течения сила внутреннего трения, действующая на боковую поверхность цилиндра, уравновешивается силами давления, действующими на его основания: Fтр = Fр или
Полагая, что у стенок (на расстоянии R от оси) имеет место полное прилипание жидкости, т.е. скорость равна нулю, получим для выделенного слоя:
Объем жидкости, протекающей через поперечное сечение трубы за 1 с (расход жидкости, объёмная скорость течения) будет определяться соотношением:
Это выражение была установлено эмпирически Гагеном (1839 г.) и Пуазейлем (1840 г.) независимо друг от друга и носит название формулы Пуазейля. Величина
где Δр играет роль напряжения, Q – силы тока, а Z – сопротивления. Из закона Пуазейля следует, что падение давления крови в сосудах (Δр = QZ = 8η l Q/πR4) обратно пропорционально R4. Не случайно, основные фармакологические средства нормализации давления направлены, прежде всего, на изменение просвета сосудов (так, нитроглицерин расслабляет мышцы артериальных стенок). Границы применимости формулы Пуазейля: 1) ламинарное течение; 2) гомогенная жидкость; 3) прямые жесткие трубки; 4) удаление от источников возмущений (изгибов, сужений, входа, выхода и т.д.). Формула Пуазейля (12) лежит в основе многих методов определения вязкости жидкостей.
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 459; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 , (3)
, (3) , (4)
, (4) . (5)
. (5) . (6)
. (6)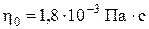 , а при 900 С и атмосферном давлении –
, а при 900 С и атмосферном давлении –  . В целом вязкость жидкости, как установил Я. И. Френкель, пропорциональна времени релаксации (η ~
. В целом вязкость жидкости, как установил Я. И. Френкель, пропорциональна времени релаксации (η ~  ), которое уменьшается с ростом температуры. Т.е. при нагревании жидкостей их текучесть должна возрастать, что подтверждается опытом. Это связано с возрастанием среднего расстояния между молекулами и, следовательно, ослаблением взаимодействия между ними.
), которое уменьшается с ростом температуры. Т.е. при нагревании жидкостей их текучесть должна возрастать, что подтверждается опытом. Это связано с возрастанием среднего расстояния между молекулами и, следовательно, ослаблением взаимодействия между ними. , (7)
, (7) , (8)
, (8) Рассмотрим ламинарное течение вязкой жидкости по трубе радиусом R. Очевидно, что слои жидкости в трубе, будут представлять собой цилиндры, расположенные коаксиально по отношению к геометрической оси трубы. Скорости разных слоев жидкости будут разными и лежат в интервале от нуля (для слоя прилипшего к стенкам трубы) до
Рассмотрим ламинарное течение вязкой жидкости по трубе радиусом R. Очевидно, что слои жидкости в трубе, будут представлять собой цилиндры, расположенные коаксиально по отношению к геометрической оси трубы. Скорости разных слоев жидкости будут разными и лежат в интервале от нуля (для слоя прилипшего к стенкам трубы) до 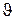 max (для слоя, который движется по оси этой трубы (см. диаграмму распределения скоростей рис.1).
max (для слоя, который движется по оси этой трубы (см. диаграмму распределения скоростей рис.1). , (9)
, (9) , откуда
, откуда 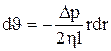 . (10)
. (10) . (11)
. (11) Из (11) видно, что скорости частиц жидкости распределены по параболическому закону, причем вершина параболы лежит на оси трубы (рис.).
Из (11) видно, что скорости частиц жидкости распределены по параболическому закону, причем вершина параболы лежит на оси трубы (рис.). . (12)
. (12) в формуле (10) называется гидравлическим сопротивлением сосуда. По аналогии с законом Ома (12) можно переписать в виде:
в формуле (10) называется гидравлическим сопротивлением сосуда. По аналогии с законом Ома (12) можно переписать в виде: , (13)
, (13)


