
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Бернулли и его физический смысл.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение неразрывности и уравнение Эйлера являются основными в механике газов. Совместное решение этих уравнений дает бесконечное количество корней. Для однозначности решения необходимо добавить уравнение, описывающие краевые условия. До сих пор удалось получить только для небольшого количества относительно простых случаев. Одним из наиболее важных случаев является уравнение Бернулли, и выводу которого мы переходим. Запишем систему дифференциальных уравнений движения (Эйлера) для элементарной струйки
При установившемся движении элементарной струйки
Умножим первое уравнение на dх, второе – на dу, третье – на dz и почленно сложим и составим эквивалентное уравнение
Оси координат разместим так, чтобы gх = gу =0, а gz = -g. Тогда уравнение примет вид
Выражение, стоящие в скобках представляют полные дифференциалы давления dР и квадрата скорости, т.е.
В следствии этого уравнение можно переписать в виде
Рассмотрим установившееся течение несжимаемого газа, т.е. такое, при котором скорости в каждой точке не меняется с течением времени ( Интегрируя это уравнение при условии ρ = сопst получим:
где Р - энергия давления (статическое давление), н/м2;
кости (динамическое давление) н/м2. Уравнение (55) часто называют уравненем энергии, т.к. размерность н/м2 представляет собой энергию 1 м3 потока движущейся жидкости или газа. Разделив все члены на ρ и g получим другой вид уравнения Бернулли:
Размерность каждого члена уравнения (56) выражается в м, а это есть энергия единицы веса Сумма ( Отношение ( Здесь: z -геометрическая высота (напор), которая выражает энергию положения;
Таким образом, полученное уравнение можно прочитать так: при установившемся движении идеальной несжимаемой жидкости вдоль линии тока сумма геометрической, пьезометрической и скоростной высот (напоров) не изменяется. С энергетической точки зрения уравнение Бернулли показывает, что сумма потенциальной и кинетической энергии идеальной несжимаемой жидкости есть величина постоянная. Полная удельная энергия остается неизменной. Екин + Епотенц = сопst (57) Таким образом уравнение Бернулли представляет собой закон сохранения механической энергии при движении идеальной жидкости. В этом смысле оно имеет фундаментальное значение для гидромеханики. В практических инженерных задачах пользуются средним значением скорости по сечению реального потока, определяя ее как отношение секундного расхода жидкостей к площади сечения потока:
Действительно, скорость в различных точках сечения отличается от этого значения на некоторую величину Δ W, различную для разных точек по абсолютному значению и по знаку. Кинетическую энергию протекающей через сечение жидкости, отнесенную к I м3 этой жидкости и определяемую через величину средней скорости, вычисляют согласно выражению:
и уравнение для потока в целом при плавно изменяющемся сечении будет иметь вид:
Коэффициент αзависит от неравномерности распределения скоростей по сечению и называется коэффициентом Кариолиса. Для ламинарного потока в круглой трубке, где распределение скоростей по сечению соответствует параболе, α=2. Для установившегося турбулентного течения в трубах.α = 1,1 - 1,13. Уравнение (58) было выведено для жидкости, а для газа - из предположения несжимаемого газа. Уравнение для идеального газа, учитывающее внутреннюю энергию газа, а также подвод или вывод тепла и предназначенное для расчетов, когда меняется температура потока, имеет вид:
где U- внутренняя энергия газов при температуре Кдж/кг Q - величина подводимого или отводимого тепла, Кдж; А - механический эквивалент тепла Энергия частиц реальной жидкости или газа, движущаяся в потоке, не будет оставаться постоянной. Часть энергии будет расходоваться на преодоление сопротивлений, возникающих вследствие вязкости. Обозначим потерянную на рассматриваемом участке энергию, отнесенную к 1 м3 движущейся реальной среды, через Δ Рп. Тогда уравнение Бернулли, написанное для двух сечений реальной жидкости, будет иметь вид
где Р -пьезометрическое давление;
|
||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 894; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

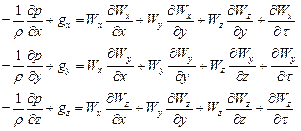 (51)
(51)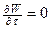 , а компоненты скорости изменяются только в направлении соответствующих осей координат. Тогда уравнение Эйлера упростится и примет вид
, а компоненты скорости изменяются только в направлении соответствующих осей координат. Тогда уравнение Эйлера упростится и примет вид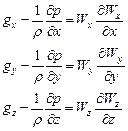 (52)
(52) (53)
(53)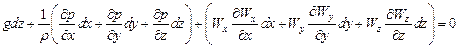
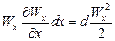
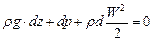 (54)
(54)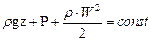 , н/м2,(55)
, н/м2,(55)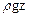 -энергия положения (геометрическое давление) н/м2;
-энергия положения (геометрическое давление) н/м2;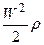 -кинетическая энергия I м3 движущегося газа или жид-
-кинетическая энергия I м3 движущегося газа или жид-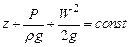 , м (56)
, м (56)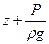 )характеризует потенциальную энергию.
)характеризует потенциальную энергию.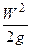 ) - кинетическую энергию струйки, отнесенную к 1 кг движущейся среды.
) - кинетическую энергию струйки, отнесенную к 1 кг движущейся среды.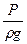 -пьезометрическая высота (напор), которая вы-ражает энергию давления, м;
-пьезометрическая высота (напор), которая вы-ражает энергию давления, м;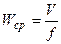
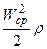
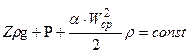 (58)
(58)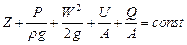 , (59)
, (59)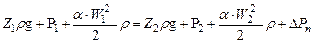 (60)
(60)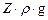 - давление положения;
- давление положения;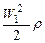 - динамическое давление.
- динамическое давление.


