
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное уравнение статики идеальнойСодержание книги
Поиск на нашем сайте
жидкости (уравнение Эйлера). Перед тем, как начать изучать движение газов, следует рассмотреть условие их равновесия. Это необходимо для выяснения условий поведения газа при малых скоростях движения, где его состояние близко к равновесному, и для получения исходных предпосылок для последующих выводов. При этом изучают зависимость давления в данной точке от объемного веса газа и геометрического положения точки. При выводе основных соотношений статики газов исходят из следующих положений:
Для вывода уравнения равновесия жидкости выделим в ней элементарный прямоугольный параллелепипед с ребрами dх, dу, dz и объемом dV=dx,dy,dz на этот параллелепипед действуют силы тяжести и силы давления, действующие на. каждую грань (рис.5). Обозначим проекции ускорения силы тяжести на оси координат через gx, gy ,gz. Тогда проекции самой силы тяжести на оси координат будут соответственно равняться
Эти силы должны быть уравновешены разностью давлений, приходящейся на соответствующие грани параллелепипеда. При переходе от одной грани к противоположной давление, в общем случае, Р должно изменяться.
И поэтому силу давления на грань «а» и на противоположную грань «в» можно записать Сила на грань «в» войдет в уравнение проекций со знаком минус. И для грани, перпендикулярной к оси X, равнодействующая сил давления равна:
Проекция объемной силы равна произведению массы ρ· dx · d y · dz на проекцию ускорения gx, если рассматривать направление по оси Х. ρ· dx · d y · dz ·gx = gx · ρ·dV (19) а сумма сил, действующих в направлении оси X равна:
Если уравнение разделим на ρ·dV, получим
Условие равновесия для всех трех координат будет иметь следующий вид:
или
Эта система носит название системы уравнений Эйлера- уравнений статики жидкости и газа. Умножил уравнение (2.17) первое на dх и последующее на dу, dz и, складывая их, получим:
Трехчлен в левой части уравнения (2.18) представляет полный дифференциал давления, поэтому
Это уравнение называют основным уравнением статики жидкостей и газов. Уравнение (2.19) содержит две неизвестных функции Р и ρ поэтому для решения необходимо еще одно урав-нение. Таким является так называемое характеристическое уравнение или уравнение состояния, которое, в общем случае, определяет зависимость плотности от давления и температуры. Таким образом для газов уравнением состояния является уравнение Клапейрона –Менделеева
где Р - абсолютное давление; R - газовая постоянная, разная для различных газов, но не зависящая от температуры и давления; Т - абсолютная температура. Если направить силу тяжести по координате у, то
Интегрируя последнее уравнение, получим:
Постоянную интегрирования С определяем из уравнения (2.21) в условиях сечения уо, где газ соприкасается с атмосферой и имеет давление Ро. Подставим вместо у = уо и Р= Ро получим
Далее можно рассмотреть два случая.
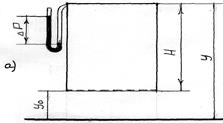
Рис.6 К определению следствий из уравнения Эйлера В первом случае (рис.6 а) газ соприкасается с воздухом снизу своего объема Обозначим разность геометрических отметок через Н = у - уо (у > у о), получим:
Р = Р о - ρ·gН Если в сосуде на высоте Н поставить V образный манометр, то он покажет разность давлений Δ Р между сосудом и окружающим воздухом, равную Δ Р= Р г – Рв
где горячего газа. Т.к. ρв >ρг, то ΔР > 0, т.е. должно быть положительное давление. Этот вывод подтверждается практикой работы печей, в которых наблюдается увеличение давления газов от пода печи к своду. Во втором случае газ соприкасается с воздухом в верхней части занимаемого объема, как видно из рисунка 6.б. При этом у > у ои Н = у о- у отсюда Р = Р о + ρ·gН Рассуждая аналогично предыдущему, будем иметь
Эта зависимость лежит в основе расчета статики дымовых труб, т.е. можно рассчитать статическое разряжение у основания дымовой трубы.
8. Уравнение неразрывности движения жидкостей и газов Теория движения газов строится из предположения неразрывности течения (сплошности). Это основное уравнение газовой динамики мы выведем.для элементарной струйки газа, поперечные размеры которой настолько малы, что в каждом ее сечении можно считать постоянным все основные параметры потока: скорость, давление, температуру и плотность газа. Чтобы получить уравнение неразрывности, рассмотрим стационарное (установившееся) движение элементарной струйки газа (рис.7). При стационарном движении в любой точке пространства сохраняются неизменными во времени скорость движения и состояние жидкости или газа (плотность, давление и температура). Траектория частиц при таком движении называется линиями тока. Боковая поверхность струйки, носящей название поверхности тока, является для жидкости (газа) непроницаемой. Рассмотрим некоторый участок элементарной струйки между двумя нормальными поверхностями тока сечениями I и 2, заметим, что в указанном на рис.7 направлении 1-2 приток газа осуществляется только через поперечное сечение I, а расход газа только через сечение 2.
За бесконечно малый промежуток времени dτ выделенная часть струйки переместится в новое положение 1´-2´. Перемещение состоит в том, что за время dτ заштрихованный объем I´-2 вместит газ, вытесненный из области I-I´, а известное количество газа за то же время вытечет из этого объема и заполнит область 2-2´. Приток газа в объеме 1´-2 составит:
где ρ1 - плотность газа в поперечном сечении I F1 - площадь поперечного сечения I. Расстояние между сечениями I и I´ равно произведению скорости движения на элементарный промежуток времени.
где W1 - скорость в сечении I, откуда
Расход газа из объема 1´-2 равен, очевидно
При установившемся режиме и отсутствии разрывов сплошности в движущейся среде приток газа должен равняться расходу:
Отсюда, после соответствующей подстановки, получаем уравнение неразрывности- закон сохранения массы для единичной струйки жидкости или газа при установившемся течении
В случае несжимаемой жидкости, т.е. при ρ = const уравнение (31.б) принимает более простую форму
Уравнение постоянства расхода газа G =g ρWF = const можно представить так же в дифференциальной форме
поделив почленно это соотношение на
В общем случае неразрывного движения сжимаемой жидкости уравнение неразрывности имеет вид
- это закон сохранения энергии.
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.119.163 (0.007 с.) |

 (17)
(17) Рис. 5 К выводу уравнения
движения Эйлера
Рис. 5 К выводу уравнения
движения Эйлера

 (18)
(18) (20)
(20) =0
=0 (21)
(21)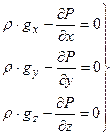 (21.б)
(21.б)
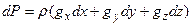 (23)
(23)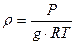 ,
, (24)
(24)
 (25)
(25)

 (26)
(26) - соответственно плотности холодного воздуха и
- соответственно плотности холодного воздуха и (27)
(27)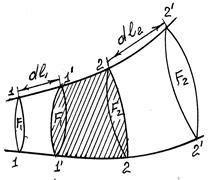 Рис.7 К выводу уравнения неразрывности
Рис.7 К выводу уравнения неразрывности
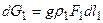 (28)
(28)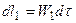 (29)
(29) (30.а)
(30.а) (30.б)
(30.б) (31.а)
(31.а) (31.б)
(31.б) (32)
(32)
 , получим
, получим (33)
(33) (34)
(34)


