
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплотехника для металлурговСодержание книги
Поиск на нашем сайте
МАСЛОВ В.А.
ТЕПЛОТЕХНИКА ДЛЯ МЕТАЛЛУРГОВ (часть 3 «Механика жидкостей и газов») Мариуполь 2009 Министерство образования и науки Украины Приазовский государственный технический Университет
МАСЛОВ В.А.
ТЕПЛОТЕХНИКА ДЛЯ МЕТАЛЛУРГОВ (часть 3 «Механика жидкостей и газов») Мариуполь 2009 УДК 669. 04(075.8) Теплотехника для металлургов. В.А Маслов Учебное пособие для вузов. Изд. ПГТУ, Мариуполь, 2009 г., с.83. В разделе «Механика жидкостей и газов» рассмотрены основные понятия, определения, закономерности и законы статики, кинематики и динамики жидкостей и газов. Рассмотрены вопросы практического использования основных положений механики жидкостей и газов в печах. Раздел «Механика жидкостей и газов» является составной частью базового курса «Теплотехника» для направления «Металлургия» и может быть рекомендован студентам этого направления в качестве учебника. Иллюстраций 28, таблиц 3, библиографий 4.
Компьютерный набор и верстка Л.н. Сапрыкина
ОГЛАВЛЕНИЕ
МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ
Введение в механику жидкости и газа От характера движения газов в печах в значительной мере зависят условия теплообмена в их рабочем пространстве, удаление продуктов сгорания и распределение давлений по дымовому тракту печи. В.Е. Грум-Гржимайло первым обратил внимание на поведение газов в печах, систематизировал сложившиеся у него на основе опыта представление о движении газов и наглядно их описал, приняв законы гидравлики и создал "Гидравлическую теорию печей". Механика газов, так же как и гидромеханика рассматривает газ и жидкости как сплошную легкоподвижную среду, которая состоит из частиц, между которыми отсутствуют свободные промежутки. Это позволяет считать распределение вещества и параметров непрерывным. Такой подход применим лишь в том случае, если возможно выделить частицы, удовлетворяющие следующим требованиям: 1. Частица должна быть настолько малой, чтобы в ее пределах частицу можно было считать однородной, т.е. во всех точках такой частицы свойства были одинаковы. 2. Частица должна быть настолько большой, чтобы она содержала очень большое число молекул и линейные размеры её были значительно больше длины свободного пробега молекул. Если невозможно выделить из рассматриваемой системы частицу, которая удовлетворяет указанным требованиям, то среду нельзя считать сплошной и необходимо учитывать молекулярное движение, т.е. использовать законы молекулярно-кинетической теории. Поэтому нет никакого принципиального различия между законами, управляющими движением газов и жидкостей. Вследствие этого механика газов использует всё то богатство, которое накопила гидравлика. Раздел механики сплошных сред, относящихся к газам и жидкостям, получил название "гидромеханики" или "механика жидкости". Раздел механики сплошных сред, относящихся к движению газов с относительно небольшими скоростями внутри камер промышленных печей, принято называть "механикой газов".
Раздел, посвященный движению газов с большими скоростями, когда существенной становится их сжимаемость, называется "газовой динамикой". Механика газов и жидкостей исходит из основных принципов физики и общей механики, причём полученные выводы они согласуют с экспериментальными исследованиями, которые одновременно дополняют и подтверждают эти выводы. При минимальном течении жидкость можно представить в виде слоев, которые скользят один относительно другого. Жидкостью называется агрегатное состояние вещества между твердым и газообразным. Жидкость характеризуется следующими свойствами: 1) сохраняет объем; 2) образует поверхность; 3) обладает прочностью на разрыв; 4) принимает форму сосуда; 5) обладает твердостью. Свойства 1-3 подобны свойствам твердых тел, а 4 - свойством газа. Главным отличительным свойством жидкости является текучесть. Газом называется агрегатное состояние вещества, в котором все его частицы слабо взаимодействуют между собой и двигаясь заполняют весь объем. Основным свойством газа является его способность заполнять весь предоставленный ему объем. Свойства жидкости и газов имеют много сходных черт и изучаются параллельно. С позиций физики капельная жидкость значительно отличается от газа с позиций механики жидкости различие между ними не так велико и часто законы, справедливые для капельных жидкостей, могут быть приложены к газам. Известно, что число молекул в 1 см3 при атмосферном давлении равно 2,7.1019, а длина свободного пробега молекулы, представляющая собой статистическое среднее расстояние, проходимое молекулами между столкновениями, будет порядка 10-5 см. Этот пример показывает, что заменяя реальную жидкость ее моделью в виде непрерывной жидкой среды, мы действительно не делаем ошибки до тех пор, пока не будем интересоваться движением молекул или состоянием внутри межмолекулярного пространства. Газы в нагревательных печах обычно находятся под давлением, мало отличающимся от атмосферного. Давление газов в различных местахпечи обычно отличается на 20÷200 н/м2, что составляет 0,02-0,2 % по отношению к абсолютному давлению, под которыми эти газы находятся. Вследствие этого изменение объема газа из-за малого изменения давления ничтожно. Изменение температуры в печах происходит постепенно и поэтому на коротких участках можно пренебречь его влиянием на изменение объема газа. Все это позволяет рассматривать газы как несжимаемые среды.
Вязкость жидкостей и газов.
Вязкостью называется свойство жидкости оказывать сопротивление сдвигу. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц жидкости. Вязкость характеризуется степень текучести жидкости или подвижности ее частиц. При ламинарном течении жидкости можно представить в виде слоев, которые скользят один относительно другого. Рассмотрим два слоя жидкости, движущиеся на расстоянии Δy друг от друга (рис.1). Один слой движется со скоростью W, а другой - со скоростью W + ΔW. Между ними возникает разность скоростей ΔW. Величина ΔWявляется абсолютным
сдвигом слоя 1 по слою 2, а
Если возьмем предел этого отношения, то получим выражение
Величина μ, аналогичная коэффициенту сдвига в твёрдых телах и характеризующая сопротивляемость жидкости сдвигу, называется коэффициентом внутреннего трения или коэффициентом динамической вязкости.
На существование уравнения (9.б) обратил своё внимание Ньютон, который и сформулировал общеизвестный закон. Касательное напряжение трения между двумя слоями прямолинейно движущейся вязкой жидкости (газа) пропорционально отнесенному к единице длины изменению скорости по нормали к направлению движения. Жидкости подчиняющиеся этому закону называются Ньютоновкими и составляют большенство всех жидкостей. Следовательно, вязкость принадлежит к числу явлений переноса импульса движения. Сила внутреннего трения в жидкости равна.
т.е. она прямопропорциональна градиенту скорости, площади трущихся слоев и коэффициенту вязкости (трение в жидкости отличается от трения в твёрдых телах, где силы трения зависят от нормального давления и не зависят от площади трущихся частей). Для определения размерности динамического коэффициента вязкости по уравнению (9.б) получим
В международной системе единиц СИ коэффициент динамической вязкости выражается в ньютон-секундах на квадратный метр (н.с/м2). В старой технической системе единиц измерения коэффициент динамической вязкости имеет размерность кг · с/см2. Вязкость жидкостей в сильной степени зависит от температуры: вязкость капельных жидкостей при увеличении температуры уменьшается, а вязкость газов возрастает. Это объясняется тем, что в газах интенсивность теплового движения (средняя скорость) молекул с повышением температуры возрастает и, следовательно, возрастает коэффициент вязкости. В капельных жидкостях молекулы не могут, как в газе, двигаться по всем направлениям, они могут лишь колебаться около своего среднего положения. С повышением температуры средние скорости колебательных движений молекул увеличиваются, благодаря чему легче преодолеваются удерживающие их связи.
Зависимость коэффициента внутреннего трения газов от температуры определяется по формуле, найденной опытным путём
где μо - вязкость газов при 0°С. Т - абсолютная температура газа. С - постоянная величина, зависящая от вида газа. Наряду с понятием абсолютной или динамической вязкости в механике газов нашло применение кинематическая вяз-кость (кинематический коэффициент вязкости) представляющий собой отношение абсолютной вязкости жидкости или газов к плотности Название кинематической вязкости вытекает из того, что в размерности этой величины отсутствуют единицы силы. В самом деле, представим размерность μ и ρ, получим:
Кинематический коэффициент вязкости капельных жидкостей при давлениях до 200 бар весьма мало зависит от давления при обычных гидравлических расчётах не учитывается. Кинематический коэффициент вязкости газов зависит от температуры и давления, возрастая с увеличением температуры и уменьшаясь с увеличением давления (табл.1)
Таблица.1 Кинематический коэффициент вязкости некоторых газов (при давлении 1,01 бар)
Важнейшими свойствами газов являются плотность и удельный объем. Плотностью называется масса единицы объема, т.е. отношение массы к ее объему
Наряду с плотностью часто используют понятие «удельный вес». Удельным весом называется вес единицы объема
В технической термодинамике и в некоторых разделах газодинамики в качестве величин, характеризующие плотностные качества газа, пользуются понятием «удельный объем», который представляет объем, занимаемый единицей массы газа
Свойства гидростатики Гидростатика изучает законы равновесия (покоя) жидкостей и газов. Представим себе сосуд, наполненный жидкостью, находящийся в покое. Мысленно выделим в этой жидкости элементарную площадку ΔS и рассмотрим условия его равновесия, приложив к нему поверхностные силы, действующие со стороны окружающей его жидкости.(рис.2)
Предположим, что на эту площадку, например, действует сила Р, направленная под некоторым углом к этой площадке. В этом случае эту силу можно было бы разложить на две составляющие: лежащую в плоскости касательную силу Рτ и нормальную силу Рп. Такие две силы (равные по величине Рп и Рт, но противоположные по направлению) действовали бы со стороны элемента А на покоящуюся жидкость. Из опыта известно, что жидкость оказывает сопротивление сжимающим нормальным усилием и в то же время способна деформироваться под действием как угодно малых касательных сил. Таким образом, существование силы Ртвызвала бы внутри жидкости течение, нарушая тем самым состояние покоя. Отсюда следует первое свойство: при покое жидкости силы, взаимодействующие между отдельными объёмами жидкости, а так же силы, с которыми покоящаяся жидкость действует на стенки сосудов, направлены перпендикулярно к поверхности, ограничивающей рассматриваемые объёмы жидкости.
Второе свойство или основная теорема гидростатики: гидростатическое давление в данной точке не зависит от того, как ориентирована площадка в пространстве, которой принадлежит данная точка. Иначе говоря, как бы мы не проводим сечение через некоторую точку вжидкости, гидростатическое давление на площадке, включающей в себя эту точку, будет отличаться только направлением, сохраняя свою величину. Для различных точек жидкости величина гидростатического давления будет различной, т.е. гидростатическое давление в точке является функцией координат.
Кинематика газов и жидкости В механике газов и жидкостей существует ряд понятий и определений, на основе которых построены основные закономерности. Рассмотрим их. Представляя себе частицу жидкости (газа) исчезающее малого объема, можно говорить о том что она находится в той или иной точке пространства. С течением времени она проходит непрерывный ряд точек, совокупность которых называется троекторией данной частицы жидкости. Поскольку в данный момент времени скорость движения частиц зависит от положения частиц в пространстве, т.е. является функцией координат, можно записать W =f (x,y,z) для данного момента времени. В проекциях на оси координат времени
В любой точке пространства скорость может изменятся во времени, тогда в самой общей форме можно записать
Под установившимся движением подразумевается такое движение жидкости (газа), при котором не только скорость но и все другие характеристики жид кости (плотность, давление, силы) не зависят от времени и остаются постоянными для каждой точке пространства. Линией тока называют воображаемую кривую, проведенную в жидкости таким образом, что каждая частица жидкости, находящаяся на ней в данный момент времени, имеет скорость, совпадающую по направлению с касательной к этой кривой. В установившемся потоке линии тока совпадают с троекториями жидких частиц (рис.3)
Введем понятие «трубка тока» или «элементарная струйка». Вообразим внутри жидкости произвольный замкнутый контур и предположим, что по своим размерам он очень мал. Через каждую точку этого контура можно провести линии тока, соответствующие данному моменту времени. В результате такого построения получим замкнутую цилиндрическую поверхность, состоящую из непрерывного ряда линий тока. Получим трубчатую поверхность, которая называется трубка тока или элементарная струйка (рис.4). Свойство трубки тока – частицы жидкости, находящиеся внутри нее не могут ни вытекать, ни втекать через ее боковую поверхность. Площадь сечения элементарной струйки, нормальное направление линий тока, называют живым сечением или просто сечением струйки. Жидкость может втекать и вытекать только через поперечное сечение струйки. Уравнения Бернулли
Истечение несжимаемых газов через отверстия часто встречаются в условиях работы нагревательных печей (истечение газа и воздуха в горелках, при выбивании газов через отверстия в стенах печей и т.д.). Рассмотрим прежде всего истечение несжимаемых газов через отверстия, причем в процессе истечения температура потока не меняется. При низких скоростях истечения (до 200 м/с) и давлении до 5000 н/м2 газ можно считать несжимаемым (условно).
Свойства свободной струи
Струя называется свободной, если она вытекает из насадка той или иной формы в неограниченное, т.е. не стесненное стенками пространство. Если физические свойства неподвижной окружающей среды и струи одинаковы, то такая струя называется затопленной Образование свободной струи обусловлено тем, что в потоке не ограниченном стенками, от воздействий поперечных турбулентных пульсаций небольшие объемы газа выбрасываются за первоначальную границу потока. Сталкиваясь с атмосферой, эти объемы вовлекают ее в движение, а их скорость уменьшается. На место выскочивших частиц в струю поступают новые из окружающей среды и подтормаживают более быстрые частицы.
Рис. 21. Схема свободной затопленной турбулентной струи
В результате этого процесса, называемого турбулентным перемешиванием, образуется пограничный слой, разделяющий неподвижную среду и ядро потока, которое сохраняет начальную скорость (рис.21) По мере удаления от сопла толщина ядра, скорость которого постоянная, уменьшается, а пограничные слои увеличиваются. Происходит выравнивание скорости в поперечном сечении. В соответствии с механизмом образования струи количество движения в ее поперечных сечениях должно оставаться постоянным. Опытами также установлено, что давление в свободной струе постоянно и равно давлению окружающей среды. Для технических расчетов можно считать, что образующие границ струи прямолинейны. Следовательно, струя представляет собой конус, вершина конуса находится внутри сопла на расстоянии Sп от его среза и называется полюсом струи. Угол раскрытия свободной струи α = 18-26°
Часть струи Sн, в которой осевая скорость сохраняет начальное значение, называется начальным участком. Участок струи, расположенный затем по течению, называется основным участком. В основном участке скорость на оси струи Wось непрерывно падает (рис.22). Опыты показывают, что расход по длине струи растет приблизительно линейно. Вслед-ствие постоянства давления количество движения во всех сечениях струи должно быть одно и то же, что и подтверждается опытом:
Кинетическая энергия уменьшается в связи с затратами на вовлечение в движение окружающей среды и снижению скорости потока. В центральной части свободной струи можно выделить ядро, каждое поперечное сечение которого характеризуется расходом, равным начальному расходу струи. Эта область струи называется ядром постоянной массы, угол его раскрытия 2,5 -2,8°. Остальная часть струи представляет собой присоединенную массу. Согласно теории свободной струи, разработанной Г.Н.Абрамовичем соотношение длины начального участка и диаметр сопла
Для скорости на оси струи в основном участке
для диаметра струи
для расхода через поперечное сечение
для скорости на расстоянии у от оси
Многочисленными опытами установлено, что распределение скорости во всех свободных затопленных струях подобно. Это следует также из приведенных выше формул. Если на график нанести зависимость относительной скорости от относительной координаты, то получаются кривые, действительные для всех струй независимо от величин dс и W. Изменение некоторых характеристик по длине струи в графическом виде представлено на рис. 21. На этом же рисунке схематически показаны профили скорости в различных сечениях струи. В струе могут находиться какие-либо примеси, концентрация которых отличается от их концентрации в окружающей среде. Температура струи может отличаться от температуры атмосферы. Выравнивание температур и концентраций с окружающей средой физически происходит так же, как и выравнивание скоростей — в результате турбулентного перемешивания (роль молекулярной диффузии обычно мала). Аналогично тому, как секундное количество движения остается постоянным по длине струи, секундная энтальпия и количество примеси в струе также сохраняют постоянные значения. Изменение избыточной температуры и избыточной концентрации на оси струи можно определить по одинаковым формулам:
18 Особенности движения газов в печах.
Существует несколько разновидностей движения газов в рабочих камерах печей: канальное, струйное, фильтрационное, Канальное движение в рабочем пространстве имеет место в печах с вытянутым рабочим пространством, когда скорости газов в различных точках его сечения направлены одинаково. В рабочем пространстве современных печей этот вид движения встречается редко. Струйное движение в камере. Возможно два случая: струя успевает заполнить сечение камеры и струя не успевает запол-нить сечение камеры. Для рабочего пространства печей чаще всего характерен второй случай. В начале камеры струя развивается аналогично свободной струе и также вовлекает в движение окружающую среду. Но т.к. стенки камеры препятствуют свободному притоку газа из атмосферы, в районе корня струи создается разрежение (как и во входной части эжектора) Перед выходом из камеры движение примерно такое же как и при ударе струи в тупик с той только разницей, что часть газа покидает камеру. По закону сохранения массы из камеры уходит столько газа, сколько входит через сопло, поэтому часть газа, которая захватывается в корне струи, поворачивается и движется по торцевой стенке. Поскольку в районе тупика давление повышенное, а в корне струи пониженное, у продольных стен образуется поток, движущийся в направлении, обратном направлению струи. В камерах со струйным движением давление изменяется и вдоль камеры и в поперечных сечениях самое низкое давление наблюдается на оси струи в области входа в камеру, самое высокое давление -на выходе из камеры. В начале камеры разница давлений у периферии и на оси больше, чем в конце, В ряде случаев движения газа в камере (по М. А. Глинкову) удобно выделить ядро постоянной массы - часть струи, в сечениях которой расход равен начальному и циркуляционные зоны, отражающие замкнутые контуры, в которых вращается газ. Иногда, например, в сушках необходимо создать равномерность температур в рабочем пространстве и это достигается за счет усиления рециркуляции продуктов сгорания (рис. 23).
Газы, выходящие из топ-ки в печное устройство подсасывают из нижней зоны печи часть отработавших газов; часть же этого газа удаляется в сборный отводящий канал. Количество подсасываемого свежей струей отработавшего газа и, таким образом, кратность циркуляции зависит от сопротивления движения газов на пути их циркуляции, скорости инжектируемых струй и скорости движения смеси в пространстве между левой боковой стенкой печи и экраном. Чем больше сопротивление, тем при прочих одинаковых условиях, течение подсасывается свежей струей отработавших газов и тем больше разность температур по высоте печи. В высокотемпературных печах рециркуляцию создают путем инжектирования газов струями, выходящими из форсунок или горелок. Фильтрационное движение наблюдается в так называемых слоевых или шахтных печах. При увеличении скорости фильтрующих газов до известного предела плотный слой начинает терять свою устойчивость. При этом наиболее мелкие составляющие материалы слоя начинают выбрасываться (выдуваться) из слоя. Предел устойчивости слоя может быть найден на основании следующих соображений. В момент отрыва частицы необходимая сила Fдолжна равняться сумме относительного веса и силы инерции частицы, т.е.
где тт и тr - соответственно массы частицы материала и газа в объеме частицы, кг; dH - элементарное перемещение частицы за время dτ. Сила сопротивления частицы будет равна
где Fт -сечение частицы, м2. Приравнивая эти два последних выражения
При увеличении скорости газов в слое сверх предельной наступает состояние, при котором все частицы слоя теряют устойчивость, расстояние между частицами увеличивается, слой в целом увеличивается в объеме, а частицы в нем энергично перемещаются по некоторым своим свойствам, такой слой напоминает жидкость, перемешиваемую продуваемым газом. Отсюда и возникло название такого состояния слоя - псевдоожижен-ный или "кипящий" слой. При дальнейшем увеличении скорости все частицы слоя переходят во взвешенное состояние, и движение газов будет происходить по законам движения двухфазной среды. Движение частиц осуществляется в режиме пневмо-транспорта. Кипящий слой является промежуточным, т.к при дальнейшем увеличении наступает момент, при котором сила любого сопротивления становится больше силы веса и псевдоожиженный слой переходит в режим пневмотранспорта.
Нагревательных печах. Алгоритм расчета механики газов состоит из следующих стадии. Зная количество продуктов горения и размеры сечений для прохода дымовых газов и их длину, определяют потери на трение на всей длине печи или же по отдельным участкам, затем величину потерь на местных сопротивлениях. После этого определяют влияние геометрического напора на сопротивление системы. Геометрический напор может быть сопротивлением, если его действие не совпадает с направлением движения горячих газов. И наоборот, геометрический напор может способствовать движению газов, если его действие совпадает с направлением движения газов, тогда он уменьшает общее сопротивление дымового тракта печи. Поэтому перед значением геометрического напора стоит знак ±. Затем следует учесть эквиваленты аэродинамических сопротивлений. Суммировав все эти сопротивления можно получить общее сопротивление дымового тракта печи ( Δ Рд тракта), которое должно быть равно тяге дымовой трубы ΔР д трубы. Из этого балансового уравнения определяют потребную высоту дымовой трубы (Нтр). Затем, учитывая необходимый запас на случай повышения производительности печи и неучтенные потери и требования санитарной техник (ΔНс.тр) определяют действительную высоту дымовой трубы (Ндтр). Так как установленная высота дымовой трубы больше, чем потребная, то и разрежение такой дымовой трубой будет иметь определенный запас, который должен уравновесится переменным аэродинамическим сопротивлением дымового клапана (шибера). При равенстве этих сопротивлений давление в печи равно заданному (Рпеч =Рзад) При нарушении такого равновесия в нагревательных печах, оборудованных автоматикой, регулятор давления изменяет переменное сопротивление дымового шибера и устанавливает равновесие системы.
ЛИТЕРАТУРА
МАСЛОВ В.А.
ТЕПЛОТЕХНИКА ДЛЯ МЕТАЛЛУРГОВ (часть 3 «Механика жидкостей и газов») Мариуполь 2009 Министерство образования и науки Украины
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.183.154 (0.015 с.) |

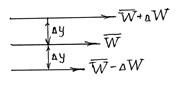 Рис.1 К понятию «внутреннее трение»
Рис.1 К понятию «внутреннее трение»
 есть градиент скорости (относительный сдвиг). Появляющиеся при этом движении касательные напряжения (сила трения на единицу площади) обозначим через τ. Тогда аналогично явлению сдвига в твёрдых телах мы получим следующую зависимость между напряжением и деформацией.
есть градиент скорости (относительный сдвиг). Появляющиеся при этом движении касательные напряжения (сила трения на единицу площади) обозначим через τ. Тогда аналогично явлению сдвига в твёрдых телах мы получим следующую зависимость между напряжением и деформацией. (9.а)
(9.а) , (9.б)
, (9.б) - градиент скорости в направлении, нормальном к слоям жидкости; τ - касательные напряжения, т.е. сила трения, отнесенная единице поверхности, которая расположится вдоль по потоку между слоями.
- градиент скорости в направлении, нормальном к слоям жидкости; τ - касательные напряжения, т.е. сила трения, отнесенная единице поверхности, которая расположится вдоль по потоку между слоями. ,(10)
,(10)  = нс/м2 или Па·с
= нс/м2 или Па·с , (11)
, (11)
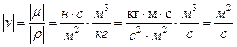
 , кг/м3
, кг/м3 , н/м3
, н/м3 , м3/кг
, м3/кг Рис. 2 Напряжение поверхностной силы
Рис. 2 Напряжение поверхностной силы
 (16.а)
(16.а) (16.б)
(16.б) Рис.3 Линии тока
Рис.3 Линии тока
 Рис. 4 Трубка тока
Рис. 4 Трубка тока

 Рис.22 Изменение количества движения (1), осевой скорости (2), расхода (3) и кинетической энергии (4) по длине свободной струи
Рис.22 Изменение количества движения (1), осевой скорости (2), расхода (3) и кинетической энергии (4) по длине свободной струи
 (102)
(102) = 4,4; (103)
= 4,4; (103) ; (104)
; (104) ; (105)
; (105) (106)
(106) (107)
(107) (108)
(108) Рис.23 Рециркуляция газов в рабочем пространстве печи
Рис.23 Рециркуляция газов в рабочем пространстве печи
 , (109)
, (109) , (110)
, (110)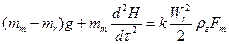
 =0 для устойчивости, тогда получим уравнение для предельно -допустимой скорости газа в слое:
=0 для устойчивости, тогда получим уравнение для предельно -допустимой скорости газа в слое: (111)
(111)


