
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные законы газового состояния и их следствияСодержание книги
Поиск на нашем сайте
Закон Паскаля. Внешнее давление, действующее на некоторый объём жидкости на каком-нибудь одном направлении, передаётся по всем направлениям не изменяя своей величины. Этот закон одинаково справедлив и для газов. Рассмотрим сосуд, наполненный жидкостью. Определим давление в точке А.
или в общем случае
где h - глубина погружения данной точки под уровень сво- бодной поверхности, на которую действует давление внешней среды. Р 0. Абсолютное давление состоит из двух частей: Р0(внешнее давление), которое передаётся по закону Паскаля всей массе жидкости, и из давления Внешнее давление, избыточное над атмосферным, действующее на частицу жидкости или газа будет называться статическим. Оно может быть положительным, так и отрицательным - меньше атмосферного. Закон Гей-Люссака. При постоянном давлении объём газа прямопропорционален, а его объёмный вес или плотность обратно пропорционален абсолютной температуре. При нагревании газа на 1 оС, при постоянном давлении, объём его увеличивается на β = 1/273= 0,00367 первоначального объёма. Из закона Гей-Люссака непосредственно следует:
где
Если имеется два объёма газа, находящихся в различных температурных условиях, то
Отношение этих объёмов равно:
из последнего равенства можно найти
и наоборот
Закон Бойля-Мариотта. При постоянной температуре газа произведение объёма на давление есть величина постоянная
РV=coпst (3)
Следовательно, Ро Vо = РV, т.е. при постоянной температуре объём изменяется в зависимости от изменения давления Закон Клапейрона-Менделеева. Уравнение Клапейрона – Менделеева объединяет два закона: закон Гей-Люсака и закон Бойля-Мариотта, характеризует состояние газа и устанавливает изменение объёма от температуры и от давления. Уравнение Клапейрона-Менделеева, в общем виде относительно 1 г моля, выражается формулой РV=RT, (4) где R - универсальнаягазовая постоянная, равная 8314,41 Дж/к моль К Универсальнаягазовая постоянная, отнесенная к 1 кг газа, имеет вид
Для М кг газа уравнение Клапейрона-Менделеева имеет вид
μ - молекулярная масса газа. Из уравнения Клапейрона-Менделеева следует, что
Связь между плотностью и давлением газа при разных температурах следующая
Уравнение для определения объёма газа при температуре Т1 и давлении Р1
Закон Архимеда. Закон Архимеда в применении к твёрдым и жидким телам гласит, что всякое тело, погружённое в жидкость, теряет в своём весе столько, сколько весит вытесненная им жидкость. Закон Архимеда в одинаковой мере относится и к газам. Если возьмём сосуд высотой Н метров и площадью ω, открытый с нижнего конца, наполненный горячим газом при температуре и окружённый холодным воздухом с температурой tо, то вследствие того, что горячий газ будет легче окружающего сосуд, холодного воздуха, то будет стремиться всплыть с силой, равной весу вытесненного им воздуха или же собственный вес горячего газа. Вес холодного воздуха, вытесненного горячим газом
Вес горячего газа, заместившего холодный воздух, будет:
Сила, с которой горячий газ стремится всплыть выражается уравнением:
Если отнести эту силу к 1 м2, то уравнение примет вид:
Вязкость жидкостей и газов.
Вязкостью называется свойство жидкости оказывать сопротивление сдвигу. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц жидкости. Вязкость характеризуется степень текучести жидкости или подвижности ее частиц. При ламинарном течении жидкости можно представить в виде слоев, которые скользят один относительно другого. Рассмотрим два слоя жидкости, движущиеся на расстоянии Δy друг от друга (рис.1). Один слой движется со скоростью W, а другой - со скоростью W + ΔW. Между ними возникает разность скоростей ΔW. Величина ΔWявляется абсолютным
сдвигом слоя 1 по слою 2, а
Если возьмем предел этого отношения, то получим выражение
Величина μ, аналогичная коэффициенту сдвига в твёрдых телах и характеризующая сопротивляемость жидкости сдвигу, называется коэффициентом внутреннего трения или коэффициентом динамической вязкости.
На существование уравнения (9.б) обратил своё внимание Ньютон, который и сформулировал общеизвестный закон. Касательное напряжение трения между двумя слоями прямолинейно движущейся вязкой жидкости (газа) пропорционально отнесенному к единице длины изменению скорости по нормали к направлению движения. Жидкости подчиняющиеся этому закону называются Ньютоновкими и составляют большенство всех жидкостей. Следовательно, вязкость принадлежит к числу явлений переноса импульса движения. Сила внутреннего трения в жидкости равна.
т.е. она прямопропорциональна градиенту скорости, площади трущихся слоев и коэффициенту вязкости (трение в жидкости отличается от трения в твёрдых телах, где силы трения зависят от нормального давления и не зависят от площади трущихся частей). Для определения размерности динамического коэффициента вязкости по уравнению (9.б) получим
В международной системе единиц СИ коэффициент динамической вязкости выражается в ньютон-секундах на квадратный метр (н.с/м2). В старой технической системе единиц измерения коэффициент динамической вязкости имеет размерность кг · с/см2. Вязкость жидкостей в сильной степени зависит от температуры: вязкость капельных жидкостей при увеличении температуры уменьшается, а вязкость газов возрастает. Это объясняется тем, что в газах интенсивность теплового движения (средняя скорость) молекул с повышением температуры возрастает и, следовательно, возрастает коэффициент вязкости. В капельных жидкостях молекулы не могут, как в газе, двигаться по всем направлениям, они могут лишь колебаться около своего среднего положения. С повышением температуры средние скорости колебательных движений молекул увеличиваются, благодаря чему легче преодолеваются удерживающие их связи. Зависимость коэффициента внутреннего трения газов от температуры определяется по формуле, найденной опытным путём
где μо - вязкость газов при 0°С. Т - абсолютная температура газа. С - постоянная величина, зависящая от вида газа. Наряду с понятием абсолютной или динамической вязкости в механике газов нашло применение кинематическая вяз-кость (кинематический коэффициент вязкости) представляющий собой отношение абсолютной вязкости жидкости или газов к плотности Название кинематической вязкости вытекает из того, что в размерности этой величины отсутствуют единицы силы. В самом деле, представим размерность μ и ρ, получим:
Кинематический коэффициент вязкости капельных жидкостей при давлениях до 200 бар весьма мало зависит от давления при обычных гидравлических расчётах не учитывается. Кинематический коэффициент вязкости газов зависит от температуры и давления, возрастая с увеличением температуры и уменьшаясь с увеличением давления (табл.1)
Таблица.1 Кинематический коэффициент вязкости некоторых газов (при давлении 1,01 бар)
Важнейшими свойствами газов являются плотность и удельный объем. Плотностью называется масса единицы объема, т.е. отношение массы к ее объему
Наряду с плотностью часто используют понятие «удельный вес». Удельным весом называется вес единицы объема
В технической термодинамике и в некоторых разделах газодинамики в качестве величин, характеризующие плотностные качества газа, пользуются понятием «удельный объем», который представляет объем, занимаемый единицей массы газа
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.172.166 (0.006 с.) |

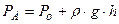
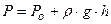 (1)
(1)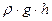 , которое обусловлено влиянием веса жидкости. Это давление называется избыточным, или относительным, или манометрическим.
, которое обусловлено влиянием веса жидкости. Это давление называется избыточным, или относительным, или манометрическим.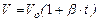 , м3/с
, м3/с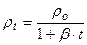 , кг/м3 (2)
, кг/м3 (2)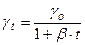 , н/м3
, н/м3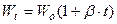 , м/с
, м/с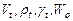 - соответственно, следующий объём, плотность, объёмный вес и скорость при данной температуре и атмосферном давлении.
- соответственно, следующий объём, плотность, объёмный вес и скорость при данной температуре и атмосферном давлении.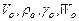 - то же, но при нормальных условиях (0°С, 0,101 мн2/ м2 или 0°С и 760 мм ртутного столба).
- то же, но при нормальных условиях (0°С, 0,101 мн2/ м2 или 0°С и 760 мм ртутного столба). и
и 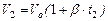
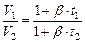
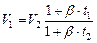
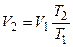
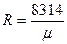 Дж/кг оК
Дж/кг оК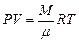 (5)
(5)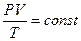 = R
= R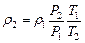 (6)
(6)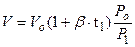 (7)
(7)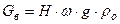 (8.а)
(8.а)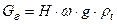 (8.б)
(8.б)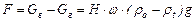 (8.в)
(8.в)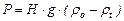 , н/м2 (8.г)
, н/м2 (8.г)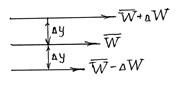 Рис.1 К понятию «внутреннее трение»
Рис.1 К понятию «внутреннее трение»
 есть градиент скорости (относительный сдвиг). Появляющиеся при этом движении касательные напряжения (сила трения на единицу площади) обозначим через τ. Тогда аналогично явлению сдвига в твёрдых телах мы получим следующую зависимость между напряжением и деформацией.
есть градиент скорости (относительный сдвиг). Появляющиеся при этом движении касательные напряжения (сила трения на единицу площади) обозначим через τ. Тогда аналогично явлению сдвига в твёрдых телах мы получим следующую зависимость между напряжением и деформацией. (9.а)
(9.а) , (9.б)
, (9.б) - градиент скорости в направлении, нормальном к слоям жидкости; τ - касательные напряжения, т.е. сила трения, отнесенная единице поверхности, которая расположится вдоль по потоку между слоями.
- градиент скорости в направлении, нормальном к слоям жидкости; τ - касательные напряжения, т.е. сила трения, отнесенная единице поверхности, которая расположится вдоль по потоку между слоями. ,(10)
,(10)  = нс/м2 или Па·с
= нс/м2 или Па·с , (11)
, (11)
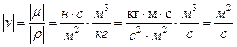
 , кг/м3
, кг/м3 , н/м3
, н/м3 , м3/кг
, м3/кг


