
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение газов с высокими скоростямиСодержание книги
Поиск на нашем сайте
Основные формулы адиабатного течения идеального газа. При движении газа с большими скоростями (обычно выше 150 м/с) в потоке возникают значительные перепады давлений, в результате чего плотность газа может сильно изменяться. Изменение плотности в свою очередь влияет на скорость, что делает невозможным применение к газам методов расчета несжимаемых жидкостей. Рассмотрим установившееся движение газа в элементарной струйке. На основании закона сохранения массы можно записать dМ 1 = dМ 2 где М 1 и М 2 – масса газа до и после истечения. Для реального газа в процессе перехода элемент dV получает тепло и совершает работу. Опуская вывод можно записать уравнение энергии движущегося газа
где qм – удельное тепло, поступающее извне; qт – удельное тепло, выделяемое в результате трения; W1,W2 – скорость в начале и конце рассматриваемого участка; z1, z2 – координаты (по вертикали) начального и конечного участка; h1,h2 – энтальпия среды в начале и конце участка; l т – работа трения. Основным для расчета одномерного движения газа является представленное уравнение (115). В большинстве задач газовой динамики изменение удельной потенциальной энергии Встречающиеся на практике случаи течения с высокими скоростями обычно не сопровождаются существенным теплообменом газа с окружающей средой, поэтому теплообменом на единицу массы газа можно пренебречь и считать течение адиабатным (qм = 0). Теплота, выделяющееся при трении, равна работе трения qт = l т). В результате из уравнения (115) получаем уравнение энергии для адиабатного течения.
Так как h = срТ, то в соответствии с уравнением (116) при адиабатном течении с возрастанием скорости газ охлаждается, а с уменьшением разогревается. Используя уравнение Клапейрона-Менделеева
а так же уравнение энтальпии
а так же значения сv и ср
где
Уравнение энергии в форме (118) связывает скорость с плотностью и давлением газа, аналогично уравнению Бернулли для несжимаемой жидкости. Если применить уравнение (118) к двум сечениям струйки, в одном из которых поток заторможен до W = 0 (или не начал движение), то с помощью формул (117.б) и (116) получим
т. е. вся кинетическая энергия переходит в энтальпию. Если торможение изоэнтропическое, то энтальпия может снова переходить в кинетическую энергию. Из уравнений (119) следует, что величины ро ρо, hо, Т о являются характеристиками данного потока. Их называют параметрами торможения. Скорость звука в газе зависит от скорости его движения. Обозначив скорость звука в неподвижном газе через ао, с помощью уравнений
т. е. что при ускорении газа скорость звука в нем уменьшается. Следовательно, поток можно разогнать настолько, что его скорость станет равной скорости звука. Такая скорость w * называется критической, а все параметры газа с критической скоростью - критическими параметрами. В газовой динамике часто используют число Маха, представляющее собой отношение скорости потока к местной скорости звука: М =W/a и коэффициент скорости, представляющий собой отношение скорости потока к критической скорости λ' = W / W* Поток, скорость которого меньше местной скорости звука (W < а, М < 1), называют дозвуковым. При W = а, М = 1 течение называется звуковым или критическим. При W > а, М > 1 течение называется сверхзвуковым, а М > 5 – гиперзвуковым. Связь между критическими параметрами и параметрами торможения описываются уравнениями
Две последние формулы справедливы только для изоэнтропного течения. При заданных параметрах торможения поток приобретет максимальную скорость, если вся энтальпия перейдет в кинетическую энергию. Согласно уравнению (119), максимальная скорость достигается при истечении в вакуум (р = 0):
Суживающееся сопло. Суживающиеся сопла служат для ускорения дозвуковых потоков газа (рис.25).
К соплу поток газа обычно подводится по трубе. Чтобы обеспечить в трубе минимальные потери энергии на трение, ее сечение выбирают достаточно большим, благодаря чему скорость получается низкой. Так как в уравнение энергии (116), которым пользуются для расчета сопла, скорости взяты в квадрате, то Скорость истечения
Проведя алгебраические преобразования, получим
Формула (124) называется уравнением Сен-Венана и Ванцеля. Расход газа через сопло определяется с помощью формулы, в которую подставляют значения ρ и w по формулам (123) и (124):
Формулы (124) и (125) применяют, когда известно давление на срезе сопла. В частности, при дозвуковом истечении оно равно давлению окружающей среды (р 1 = ра). При достижении критической скорости (w = w*) в сопле устанавливается критическое давление (р1 = р * ), которое, как указывалось, зависит только от давления торможения. Подставив в формулы (124) и (125) отношение р * /ро из формулы (121.б), получим для критической скорости выражение (121.а), а для критического расхода следующую формулу:
Если повышать давление перед соплом (р0) при постоянной температуре Т0 (это часто встречается на практике), то согласно формуле (126) для данного газа
т. е. при истечении с критической скоростью массовый расход прямо пропорционален давлению перед соплом. Практически сопла не обеспечивают расчетные характеристики потока. Поэтому истинный расход получают, умножая теоретический расход на коэффициент расхода μс ≈ 0,92. Обычно центральный угол сужения сопла принимают в пределах 30-60°. Во избежание излишних потерь энергии поверхность сопла необходимо делать гладкой без заусенцев и шероховатости. Сверхзвуковое сопло (сопло Лаваля). В ряде устройств (форсунках, фурмах, эжекторах, реактивных двигателях и др.) желательно иметь сверхзвуковые скорости истечения. Для создания таких скоростей применяют сопла Лаваля.
Сверхзвуковое сопло состоит из сужающейся и расширяющейся частей (рис.26). В соответствии с уравнением Гюгонио в сужаю-щейся части скорость газа может возрасти до критического значения, которое достигается в самом узком сечении, называемом критическим. В расширяющейся части должно происходить дальнейшее ускорение газа до сверхзвуковых скоростей. Течение газа в сужающейся части подчиняется тем же законам, что и в простом сопле. Близкие к расчетным характеристики можно получить с помощью сопел, имеющих сложный профиль. Однако ради простоты изготовления сужающуюся и расширяющуюся части выполняют коническими. Центральный угол сужения равен 30-60°, центральный угол расширения 8-14°. Сопряжение конусов закругляют, но так, чтобы фактическое проходное сечение горловины равнялось критическому. Фактические скорость и расход через сопла меньше расчетных. Поэтому расход по формуле (126) следует умножить на коэффициент расхода μс ≈ 0,92., а скорость по формуле (124) - на коэффициент скорости φ = 0,95.
22 Основы расчета механики газов в печах.
Для правильной тепловой работы нагревательных печей необходимо, чтобы на ее поду имело бы место нулевое или слабоположительное статическое давление (1-2 н/м). Сложный характер движения газов в ограниченном пространстве нагревательных печей определяет существование не менее сложного поля статических давлений. Это поле создается в результате взаимодействия тяги дымовой трубы или дымососа, влияния геометрического напора в рабочем пространстве и взаимодействия движущихся потоков газов. Давление в печи устанавливается в результате наложения друг на друга трех его составляющих:
где Рвн - поле давлений, создаваемое внешними факторами (окружающая атмосфера, дымовая труба, дымосос, эжектор и др.). РW = f(x,y,z,w) - поле давлений, возникающее вследствие дина- мики газов; РZ = f(x,y,z,t) -поле давлений создаваемое геометрическим на- пором, зависит от температуры и физических свойств газа. По закону Паскаля такое давление одинаково распространяется на все точки ограниченного пространства. Эту составляющую можно охарактеризовать как уровень давления Геометрический напор возникает в результате разности плотностей горячих газов (ρг) в рабочем пространстве печи и окружающего холодного воздуха (ρв) (рис.27). Он сравнительно легко вычисляется по формуле: РZ = f(x,y,z,t) = Нпеч g(ρв - ρг) (128) где Нпеч - высота рабочего пространства печи от пода до свода, м Обычно при управлении гидравлическим режимом печи в качестве импульса для управления измеряют статическое давление под сводом печи, а не положение кулевой линии. Величина этого импульса обычно составляет 10-30 н/м2 и определяется конкретно для каждой печи с таким расчетом, чтобы при взаимодействии составляющих и РW нулевая линия находилась бы на уровне пода печи или же несколько ниже, чтобы исключить попадание холодного воздуха в рабочее пространство печи.
Расчет механики газов в печах проводится с целью определения необходимого разрежения, создаваемого дымовой трубой или дымососом. Определив эту величину и зная расход продуктов горения и их температуру определяют размеры дымовой трубы или тип дымососа вместе с его конструктивными размерами. При этом предполагается, что на поду печи должно быть нулевое и слабо положительное давление (около 1,0 - 2,0 н/м2). Если охлаждающиеся дымовые газы движутся сверху вниз, то перед формулой геометрического давления необходимо поставить знак «+», а если снизу вверх, то знак «-«[ ± z·g (ρв – ρд.г)] Расчет механики газов в печах основан на допущении, что сопротивление системы в целом есть сумма сопротивлений отдельных, последовательно расположенных ее участков и что изменение внутренней энергии движущейся среды без особых погрешностей не учитывается. Потери энергии при движении дымовых газов по дымовому каналу (тракту) складываются из суммарных потерь на трение
Это обеспечивается соблюдением условия – тяга дымовой трубы должна быть равна сумме потерь энергии придвижении дымовых газов по дымовому каналу и дымовой трубе, т.е Для печей с переменным расходом топлива сопротивление по дымовому тракту печи обычно подсчитывают по среднему расходу топлива, умножая на величину
Определив сопротивление системы дымового тракта печи, следует рассчитать потребное разрежение, создаваемое дымовой трубой и ее размеры или же определить параметры работы дымососа (тип, мощность число оборотов и др.). Для определения потребного разрежения дымовой трубы используют уравнение Бернулли (рис.28). Принимая для сечения 1-1 Z 1= 0 и для сечения II-П Z 1= Нтр получаем (для средней температуры газов в трубе)
Кроме того,
где Ро - давление воздуха на уров-не сечения 1-1, н/м2, ρв - плотность окружающего тру-бу воздуха, кг/м3. Подставим значение Р2из уравнения (132) в уравнение (131) и получим:
Из последнего уравнения определим ΔРтр = Ро-Р1, которое представляет собой превышение давления атмосферы на уровне 1-1 над давлением газов в трубе, называемое разрежением или тягой дымовой трубы.
Из уравнения (133) видно, что величина тяги дымовой трубы зависит от высоты дымовой трубы и разности плотностей воздуха и дымовых газов, что в свою очередь определяется температурами продуктов горения в дымовой трубе и окружающего воздуха. Температура окружающего воздуха изменяется в зависимости от климатических условий и влияет на его плотность
Расчет ведут обычно на худший вариант, т.е. на работу в летнее время года, т.к. при повышении температуры окружающего воздуха его плотность становится меньше и при этом, конечно, снижается и тяга дымовой трубы. Используя уравнение (131), определяют потребную высоту дымовой трубы (затем и остальные размеры), т.е.
Для определения плотности продуктов горения в дымовой трубе требуется определить их среднюю температуру и она вычисляется по формуле:
Здесь t 1 г - температура уходящих газов у основания дымовой трубы, °С; НТр - высота дымовой трубы, м; Сt - скорость падения температуры дымовых газов по вы- соте дымовой трубы, °С/м. (для кирпичных труб Сt = 1,5 - 2,5 °С/м, для металлических труб Сt = 3 - 4 °С/м). При определении сечения устья дымовой трубы принимают скорость дымовых газов равной Wо=2,5 - 4 м/сек. Соотношение диаметра устья и оснований выбирается с точки зрения обеспечения строительной прочности. Существует определенное соотношение между диаметром основания и устья трубы, которое для кирпичных труб обычно равно Dосн=1,5 Dу. Окончательно, высоту дымовой трубы берут обычно с запасом 25%для покрытия неучтенных потерь и возможности увеличения ее пропускной способности на случай необходимости увеличения производительности печи Высота трубы должна соответствовать санитарным нормам проектирования промышленных предприятий. Высота трубы, через которую убирают продукты сгорания агрегатов с тепловой мощностью до 100 мвт должна быть не менее 30 м, а при тепловой мощности агрегатов (100-350) мвт не менее 45 м. Если же в радиусе 200 м от трубы расположены здания высотой более 15 м, высота трубы должна быть не менее 45 м независимо от тепловой мощности агрегатов. В этом случае, если одна дымовая труба обслуживает несколько печей, расчет ведут на суммарное количество дымовых газов и определяют необходимую величину тяги дымовой трубы по дымовому тракту печи, имеющему наибольшее сопротивление. В ряде случаев нагревательные устройства работают с искусственной тягой, создаваемой дымососом или вентилятором (тяга непрямого действия), струйным аппаратом. При выборе дымососа или вентилятора необходимо руководствоваться следующими положениями: 1. Производительность дымососа или вентилятора должна равняться
2. Напор, создаваемый вентилятором, дан в справочнике при плотности ρ =1,2 кг/м3. При меньшей объемной плотности он снижается пропорционально фактической плотности, равной
3. Общий напор, развиваемый вентилятором или дымососом Нобщ равен: Нобщ = Нвсас + Ннагнет где Нвсас и Ннагнет - разрежение во всасывающей трубе и давле- ние в нагнетательной трубе. 4. Затем переходят к выбору серии и номера дымососа и вентилятора. Их выбирают в зависимости от назначения машин и аэродинамической характеристики сети. Так как тяга дымовой трубы при проектировании предусматривается с запасом, а изменение расхода топлива является переменной величиной, что влияет в свою очередь на аэродинамическое сопротивление дымового тракта печи, то на нем совершенно необходимо иметь управляемое переменное аэродинамическое сопротивление. И таким переменным управляемым аэродинамическим сопротивлением является дымовой шибер (клапан) или же направляющий аппарат котла-утилизатора, которые устанавливаются на дымовом тракте печи. Величина сопротивления дымового клапана (шибера) изменяется от нуля (дымовой клапан полностью открыт) до бесконечности (дымовой клапан полностью и плотно перекрыл путь движения горячих газов). Изменяя положение дымового клапана, можно поддерживать давление в рабочем пространстве печи на заданном уровне.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.58 (0.008 с.) |

 , Дж/кг (115)
, Дж/кг (115) мало по сравнению с изменением кинетической энергии
мало по сравнению с изменением кинетической энергии  . Поэтому второй член правой части уравнения (115) принимают равным нулю.
. Поэтому второй член правой части уравнения (115) принимают равным нулю.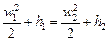 (116)
(116)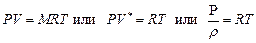 , (117а)
, (117а) , (117б)
, (117б) , (117.в)
, (117.в) , представим уравнение (1-94) в механической форме:
, представим уравнение (1-94) в механической форме: (118)
(118) , (119)
, (119) и (119) получим
и (119) получим (120)
(120) (121.а)
(121.а)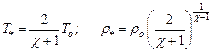 (121.б)
(121.б)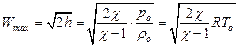 (122)
(122) Рис. 25 Скорость и давление газа при истечении через простое сопло
Рис. 25 Скорость и давление газа при истечении через простое сопло

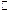
 . Таким образом, скорость в трубе перед соплом W 0 можно считать равной нулю, а давление и плотность газа равными соответствующим параметрам торможения. На коротком участке сопла можно пренебречь теплообменом и потерями энергии на трение и считать течение изоэнтропическим.
. Таким образом, скорость в трубе перед соплом W 0 можно считать равной нулю, а давление и плотность газа равными соответствующим параметрам торможения. На коротком участке сопла можно пренебречь теплообменом и потерями энергии на трение и считать течение изоэнтропическим. из сопла можно найти из уравнения (119), заменив в нем величину ρ1 с помощью уравнения адиабаты
из сопла можно найти из уравнения (119), заменив в нем величину ρ1 с помощью уравнения адиабаты (123)
(123)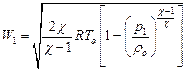 (124)
(124) (125)
(125) (126)
(126)
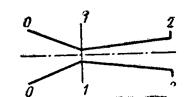 Рис. 26 Схема сопла Лаваля
Рис. 26 Схема сопла Лаваля
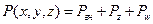
 (127)
(127)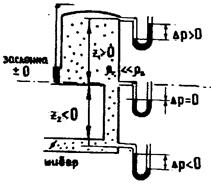 Рис.27 Статика двух газов
Рис.27 Статика двух газов
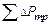 , суммарных местных сопротивлений и изменения кинетической энергии потока
, суммарных местных сопротивлений и изменения кинетической энергии потока (129)
(129)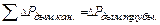

 (130)
(130) Рис. 28 К выводу разряжения дымовой трубы
Рис. 28 К выводу разряжения дымовой трубы
 (131)
(131) (132)
(132)
 (133)
(133)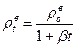 , кг/м3
, кг/м3 (134)
(134)
 , м3/с
, м3/с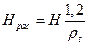 , н/м2
, н/м2


