Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение скорости потока и расхода жидкостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
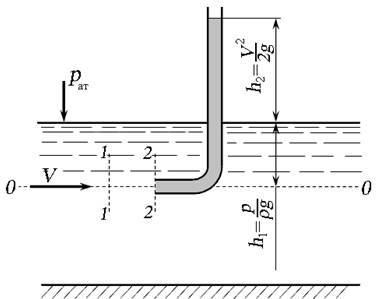
Рассмотрим применение уравнения Бернулли для измерения скорости потока с помощью таких несложных приборов, как трубка Пито - Прандтля, расходомер Вентури. Для определения скорости безнапорного потока (например, в канале) используют трубку Пито, которая представляет собой изогнутую под прямым углом трубку небольшого диаметра, устанавливаемую в потоке открытым нижним концом навстречу движению жидкости (рис. 3.9).
Рис. 3.9. Трубка Пито
Плоскость сравнения 0 - 0 расположим по оси горизонтальной части трубки. Выберем сечение 1 - 1 на некотором расстоянии от трубки, и сечение 2 - 2 на входе в трубку. Геометрические высоты центра тяжести сечений z 1 и z 2 равны нулю. В центре тяжести сечения 1 - 1 жидкость обладает кинетической энергией При попадании частиц жидкости в трубку их скорость становится равной нулю, кинетическая энергия переходит в потенциальную, и жидкость в трубке поднимется над свободной поверхностью на высоту h 2, равной скоростному напору. В центре тяжести сечения 2 - 2 жидкость обладает потенциальной энергией высоты столба жидкости h 1, и потенциальной энергией, равной кинетической. Составим уравнение Бернулли без учёта потерь напора h пот:
Скорость движения жидкости
где h - высота столба жидкости в трубке над уровнем свободной поверхности. Давление в трубке на уровне свободной поверхности создано за счёт кинетической энергии потока жидкости:
где р д - гидродинамическое давление. Давление жидкости, создаваемое скоростным напором, называется гидродинамическим давлением. Для определения скорости напорного потока рассмотрим применение трубки Пито - Прандтля, которая представляет собой совмещённые в один прибор трубку Пито и обычный пъезометр (рис. 3.10). Высота столба жидкости в трубке Пито образована за счёт гидростатического и гидродинамического давления, в пъезометре - только гидростатического.
Рис. 3.10. Трубка Пито - Прандтля
Разность уровней жидкости в трубках ∆h даёт значение скоростного напора
Расходомер Вентури представляет собой плавно сужающуюся и расширяющуюся цилиндрическую вставку устанавливаемой в трубе (рис. 3.11). В расширенной и в суженной частях расходомера установлены пъезометры.
Рис. 3.11. Расходомер Вентури
Составим уравнение Бернулли относительно плоскости сравнения, совпадающей с осью расходомера. Сечения выберем в местах подключений пъезометров. Так как центр тяжести сечений лежит в плоскости сравнения, геометрические высоты z 1 и z 2 равны нулю. Для идеальной жидкости без учёта потерь напора h пот уравнение Бернулли примет вид:
Из уравнения неразрывности потока:
Подставим значение скорости V 2 из уравнения (3.11) в уравнение (3.12):
Так как скорость V 1 - это скорость потока идеальной жидкости, то расход, определённый с этой скоростью, будет теоретическим:
где С т - теоретическая постоянная расходомера. Действительный расход жидкости:
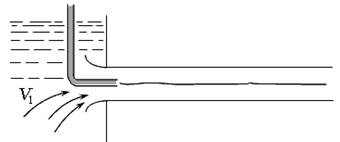
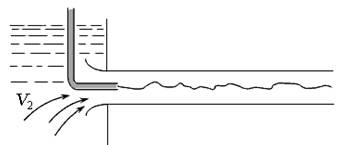
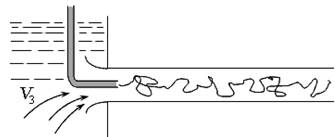
где С - действительная постоянная расходомера; k - коэффициент, который учитывает потери напора при движении жидкости в расходомере, определяется опытным путём. Режимы течения жидкости Существуют два режима течения жидкости - ламинарный и турбулентный. Движение жидкости, при котором отсутствуют изменения (пульсации) векторов местных скоростей, называют ламинарным (от латинского слова «lamina» – слой). Жидкость при этом рассматривается как совокупность отдельных слоёв, движущихся с разными скоростями, не перемешиваясь друг с другом. Движение жидкости, при котором происходят изменения (пульсации) векторов местных скоростей, приводящие к перемешиванию жидкости, называют турбулентным (от латинского слова «turbulentus» – беспорядочный, хаотичный). Исследование течений жидкости в круглой трубе провёл О. Рейнольдс в 1883 году на установке, изображённой на рис. 3.12. В начале стеклянной трубы он поместил тонкую трубку с подкрашенной жидкостью, плотность которой была равнозначна плотности основного потока жидкости. При небольшой скорости течения струйка подкрашенной жидкости двигается практически прямолинейно и горизонтально, что доказывает слоистое (ламинарное) течение жидкости (рис. 3.12, а).
а)
б)
в) Рис. 3.12. Режимы течения жидкости: а) - ламинарный; б) - переходный; в) - турбулентный
При увеличении скорости течения основного потока струйка приобретает волнистый характер, у неё появляются разрывы, что характерно для неустойчивого, переходного режима (рис. 3.12, б). При дальнейшем увеличении скорости основного потока подкрашенная струйка полностью смешивается с жидкостью, что доказывает беспорядочное (турбулентное) течение (рис. 3.12, в). Для характеристики режима течения жидкости принят безразмерный критерий - число Рейнольдса Re. Для круглых труб диаметром d:
где ν - коэффициент кинематической вязкости. На основании опытов для круглых труб при напорном течении критическое число Рейнольдса, при котором турбулентный режим переходит в ламинарный, равно Re = 2300. Скорость потока жидкости, соответствующая смене режима течения, называется критической скоростью. Для практических расчётов принято считать: - при Re < 2300 существует ламинарный режим течения; - при Re > 2300 существует турбулентный режим течения. Вместо диаметра в число Рейнольдса может входить другой линейный параметр, характерный для данного живого сечения. Для труб некруглой формы или для безнапорного потока, образующего свободную поверхность, характерным линейным размером является гидравлический радиус R, определяемый соотношением (3.1):
Критическое число Рейнольдса, записанное по гидравлическому радиусу, равно Re ≈ 580.
Рис. 3.13. Эпюра скоростей при ламинарном режиме
Для ламинарного режима течения эпюра местных скоростей по живому сечению имеет вид параболы (рис. 3.13), средняя скорость V потока в два раза меньше максимальной ( Турбулентный режим движения характеризуется непрерывным перемешиванием частиц жидкости. Скорости частиц в любой точке потока непрерывно и постоянно изменяются во времени, то есть пульсируют по величине и направлению относительно среднего значения. Для турбулентного режима характерны такие понятия, как мгновенная и осреднённая скорость. Мгновенная скорость u - это скорость частицы жидкости в данной точке в данный момент времени. Так как мгновенная скорость хаотична во времени, её можно разложить в трёхмерной системе координат на продольную ux, поперечные uy и uz ( Осреднённая скорость
Рис. 3.14. График пульсации мгновенной местной скорости:
Рассмотрим график изменения продольной мгновенной скорости ux во времени (рис. 3.14). Величина осреднённой (во времени) скорости
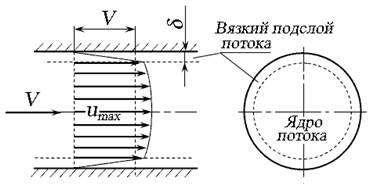
В живом сечении при турбулентном режиме различают ядро потока, в котором местные осреднённые скорости изменяются незначительно, и вязкий подслой потока толщиной δ (дельта), (рис. 3.15). Средняя скорость потока равна
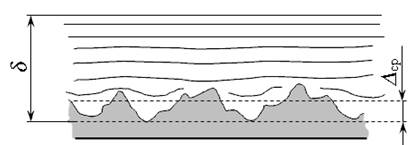
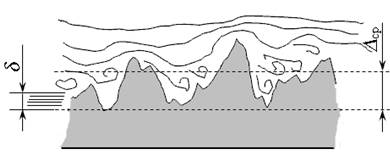
Рис. 3.15. Схема течения жидкости при турбулентном течении Вязкий подслой потока иначе называют ламинарным подслоем. Соотношение высоты шероховатости внутренних стенок трубопровода и ламинарного подслоя потока характеризует ограничивающие жидкость поверхности как гидравлически гладкие, или гидравлически шероховатые. За высоту шероховатости стенок принимают среднюю высоту ∆ср.
а)
б) Рис. 3.16. Шероховатость поверхности при турбулентном движении: а) - гидравлически гладкая; б) - гидравлически шероховатая
Если толщина ламинарного подслоя значительно больше, чем средняя высота шероховатости (δ > ∆ ср), то такую поверхность называют гидравлически гладкой (рис. 3.16, а). В этом случае шероховатость не влияет на сопротивление движению жидкости. Если толщина ламинарного подслоя меньше выступов средней шероховатости (δ < ∆ ср), то такую поверхность называют гидравлически шероховатой (рис. 3.16, б). В этом случае при обтекании выступов шероховатости усиливается турбулизация потока, что приводит к увеличению сопротивления движения жидкости и потерь напора.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 3219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.63.186 (0.012 с.) |

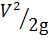 и потенциальной
и потенциальной 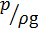 за счёт высоты столба жидкости h 1, где р - гидростатическое давление.
за счёт высоты столба жидкости h 1, где р - гидростатическое давление.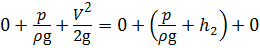 , откуда
, откуда .
.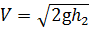 . В действительности скорость будет несколько меньше, так как вычисления были произведены без учёта потерь напора. Для определения действительной скорости потери напора учитывают коэффициентом скорости φ, который определяют экспериментально. С учётом коэффициента:
. В действительности скорость будет несколько меньше, так как вычисления были произведены без учёта потерь напора. Для определения действительной скорости потери напора учитывают коэффициентом скорости φ, который определяют экспериментально. С учётом коэффициента: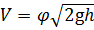 , (3.9)
, (3.9) , откуда
, откуда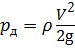 , (3.10)
, (3.10)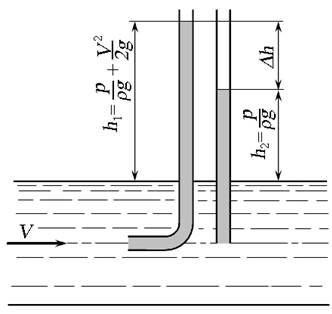
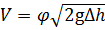 . (3.11)
. (3.11)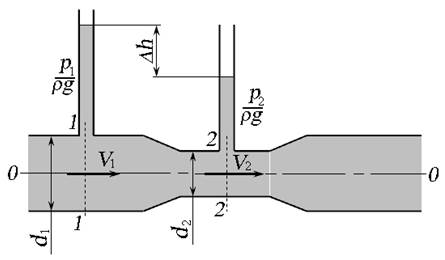
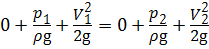 ,
,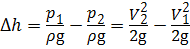 , откуда
, откуда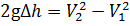 . (3.12)
. (3.12)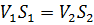 , откуда
, откуда 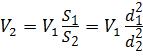 . (3.13)
. (3.13)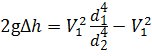 , откуда
, откуда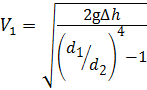 .
. ,
,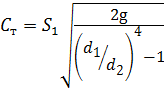 ,
,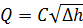 , (3.14)
, (3.14) ,
,
 , (3.15)
, (3.15)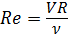 . (3.16)
. (3.16)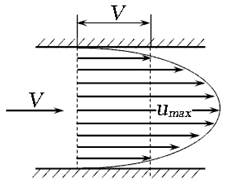
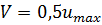 ). Коэффициент Кориолиса для ламинарного режима движения жидкости α = 2.
). Коэффициент Кориолиса для ламинарного режима движения жидкости α = 2.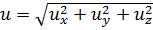 ). Мгновенное изменение величины и направления скорости частицы называют пульсацией.
). Мгновенное изменение величины и направления скорости частицы называют пульсацией.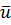 - это средняя во времени скорость частицы в данной точке, полученная за достаточно большой промежуток времени.
- это средняя во времени скорость частицы в данной точке, полученная за достаточно большой промежуток времени.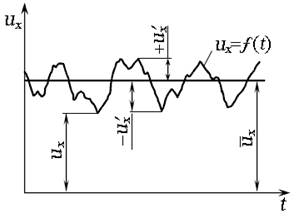
 - мгновенная скорость;
- мгновенная скорость; 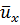 - осреднённая скорость;
- осреднённая скорость;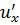 - пульсационная скорость
- пульсационная скорость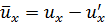 .
.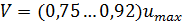 , коэффициент Кориолиса α = 1.
, коэффициент Кориолиса α = 1.