
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон Ома для неоднородного участка цепи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Обобщенный закон Ома в интегральной форме.
2. Частные случаи
3. Правила Кирхгофа для расчета разветвленных цепей.
Основы теории Максвелла. 1. Вихревое электрическое поле.
2. Первое уравнение Максвелла.
3. Ток смещения.
Плотность тока смещения -. Максвелл ввел понятие полного тока, равного сумме токов проводимости и смещения -.
4. Второе уравнение Максвелла. 5.
Контур с током в магнитном поле. Взаимодействие контуров с током.
· 1. ,,.
2. Момент силы, действующий на контур с током:
3. Энергия контура с током во внешнем магнитном поле: · Случай неоднородного поля: 1.
Если магнитное поле изменяется только вдоль оси x, контур втягивается в более сильное поле. Контур выталкивается в более слабое поле, если вектора антипараллельны. 2.
3. Работа по перемещению контура с током: Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром (или на его потокосцепление). Закон Био-Савара-Лапласа 1. Величина, показывающая, во сколько раз магнитная индукция в данной среде больше или меньше, чем в вакууме (воздухе), называется относительной магнитной проницаемостью среды: µ=B/B0. Относительная магнитная проницаемость безразмерная величина. 2. Величина, характеризующая магнитное поле и не зависящая от среды, в которой оно возбуждается, получила название напряженности магнитного поля H. Для вакуума (воздуха) физические величины В0 и Н связаны между собой равенством: B0= µ0*H. Единица напряженности магнитного поля – ампер на метр (А/м). Индукция магнитного поля в среде с магнитной проницаемостью µ равна 3. 4. Закон Био-Савара-Лапласа поле прямого проводника
Закон Био-Савара-Лапласа поле соленоида
Теорема о циркуляции 1. Понятие циркуляции.
Циркуляция напряженности эл поля всегда равна 0,следовательно,электростатическое поле потенциально и может быть ох-на потенциалом. Циркуляция магнитной индукции отлична от нуля, если контур, по которому берется циркуляция, охватывает ток. 3. Закон полного тока.
Циркуляция вектора H по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых этим контуром. Циркуляция вектора намагниченности J по произвольному замкнутому контуру равна току намагниченности Iм, охватываемому этим контуром 2. Примеры применения теоремы
Магнитное поле тороида в вакууме: 17. Заряд, движущийся в магнитном поле. 1. Магнитное поле движущегося заряда.
2. Действие магнитного поля на движущийся заряд.
Сила Лоренца, действующая со стороны магнитного поля на движущийся заряд, равна (в скалярной и векторной формах). Так как сила Лоренца всегда направлена перпендикулярно вектору скорости частицы, то она не изменяет величину скорости, а изменяет лишь направление движения частицы, т.е. по физической сути является центростремительной силой. Действие этой силы не приводит к изменению энергии заряженной частицы, т.е. эта сила не совершает работы. 3. Варианты движения заряженных частиц в магнитном поле. Заряженная частица влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции. Если скорость изменяется только по направлению, движение с постоянным по величине нормальным ускорением представляет собой равномерное движение по окружности aн=v2/R. В случае когда частица влетает в поле не под прямым углом состовляющая силы лоренца в направлении В равна 0. Таким образом движение можно представить: перемещение вдоль В с постоянной скоростью и равномерным вращением в плоскости, перпендикулярной к вектору В. R=(mvsinα)/qB траектория движения представляет собой спираль.
4. Эффект Холла Эффект Холла: если металлическую пластинку, вдоль которой течет постоянный эл ток, поместить в перпенд. к ней магнитное поле, то возник разность потенциалов. Uн=
Электромагнитная индукция. 1. Поток вектора магнитной индукции.
Магнитный поток, создаваемый контуром с током через поверхность, ограниченную им самим, всегда положителен. Теорема Гаусса для магнитного поля в вакууме: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю. 2. Потокосцепление. Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром (или на его потокосцепление). Магнитный поток через поверхность, ограниченную замкнутым контуром называется потокосцеплением Y этого контура. 3. Закон Фарадея и правило Ленца. · Направление индукционного тока определяется по правилу Ленца: при всяком изменении магнитного потока сквозь поверхность, натянутую на замкнутый проводящий контур, в последнем возникает индукционный ток такого направления, что его магнитное поле противодействует изменению магнитного потока.
4. Вращение рамки в магнитном поле.
Если рамка движется в неоднородном магнитном поле. Число линий индукции, пересекающих рамку, изменяется. В рамке возникает электрический ток. 5. Электродвигатель и генератор.
Закон Ампера 1.
где I – сила тока, l – длина проводника, α – угол между направлениями тока и вектора индукции магнитного поля. Эта формула справедлива для прямолинейного проводника и однородного поля. Сила тока 1 А – сила такого тока при прохождении которого по двум параллельным проводникам расположенным на расстоянии 1 м друг от друга возникает сила взаимодействия на каждый метр длины проводника Если проводник имеет произвольную форму и поле неоднородно, то dF=IBdlsin(dl,B). 2. Если по проводникам текут токи в одинаковых направлениях, то проводники притягиваются, а если в противоположных – отталкиваются. 3. Работа по перемещению проводника с током в магнитном поле. Элементарная работа перемещения равна произведению dA = Fdx или dA = BIldx = BIdS = IdФ. Работа, совершаемая при перемещении проводника с током в магнитном поле, равна произведению силы тока на магнитный поток сквозь поверхность, описываемую проводником при его движении. В более общем случае, когда I есть функция времени или B в пространстве движения проводника изменяется, работа перемещения определяется интегрированием dA = IdФ, в которой В или (и) I записываются в виде соответствующих функций.
Энергия магнитного поля. 1.
2. Явление само- и взаимной индукции. Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией:
Взаимной индукцией называется явление возбуждения ЭДС электромагнитной индукции в одной электрической цепи при изменении электрического тока в другой цепи или при изменении взаимного расположения этих двух цепей. Экспериментальное исследование взаимной индукции позволило установить следующее: – взаимная индуктивность зависит только от формы, размеров и взаимного расположения контуров; – магнитное потокосцепление контуров не зависит от того, по какому контуру протекает ток, создающий магнитное поле. 3. Трансформатор ЭДС самоиндукции при замыкании или размыкании цепи постоянного тока.
4.
Плотность энергии магнитного поля в общем случае:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 644; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.107.223 (0.013 с.) |


 Закон Ома для неоднородного участка цепи в интегральной форме является обобщенным законом Ома:.
Закон Ома для неоднородного участка цепи в интегральной форме является обобщенным законом Ома:.







 Первое правило Кирхгофа-алгебраическая сумма токов, сходящихся в узле, равна нулю. Узлом электрической цепи называется любая точка разветвления цепи, в которой сходится не менее трех проводников с током. Ток, входящий в узел, считается положительным, а ток, выходящий из узла - отрицательным.
Первое правило Кирхгофа-алгебраическая сумма токов, сходящихся в узле, равна нулю. Узлом электрической цепи называется любая точка разветвления цепи, в которой сходится не менее трех проводников с током. Ток, входящий в узел, считается положительным, а ток, выходящий из узла - отрицательным. Второе правило Кирхгофа - в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов I на сопротивление R соответствующих участков этого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре.
Второе правило Кирхгофа - в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов I на сопротивление R соответствующих участков этого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре.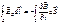 Всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре (первое основное положение теории Максвелла). аналогично магнитному полю и всякое изменение электрического поля вызывает в окружающем пространстве вихревое магнитное поле (второе основное положение теории Максвелла).
Всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре (первое основное положение теории Максвелла). аналогично магнитному полю и всякое изменение электрического поля вызывает в окружающем пространстве вихревое магнитное поле (второе основное положение теории Максвелла). Суммарное электрическое поле складывается из электрического поля, создаваемого зарядами Eq и вихревого электрического поля EB. Поскольку циркуляция Eq равна нулю, то циркуляция сумм-го поля:
Суммарное электрическое поле складывается из электрического поля, создаваемого зарядами Eq и вихревого электрического поля EB. Поскольку циркуляция Eq равна нулю, то циркуляция сумм-го поля:
 Поскольку магнитное поле есть основной, обязательный признак всякого тока, то Максвелл назвал переменное электрическое поле током смещения, в отличие от тока проводимости, обусловленного движением заряженных частиц.
Поскольку магнитное поле есть основной, обязательный признак всякого тока, то Максвелл назвал переменное электрическое поле током смещения, в отличие от тока проводимости, обусловленного движением заряженных частиц. Если в проводнике имеется переменный ток, то внутри проводника существует переменное электрическое поле, существует и ток проводимости, и ток смещения, а магнитное поле проводника определяется суммой этих двух токов.
Если в проводнике имеется переменный ток, то внутри проводника существует переменное электрическое поле, существует и ток проводимости, и ток смещения, а магнитное поле проводника определяется суммой этих двух токов.
 Полная система уравнений Максвелла для электромагнитного поля.
Полная система уравнений Максвелла для электромагнитного поля.





 На рамку с током I помещенную в магнитное поле, действует момент сил:
На рамку с током I помещенную в магнитное поле, действует момент сил: Случай однородного поля:
Случай однородного поля: Сила, действующая на контур с током:
Сила, действующая на контур с током:


 ,,
,,


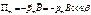
 Контур с током во внешнем неоднородном магнитном поле:
Контур с током во внешнем неоднородном магнитном поле:
 ,,,
,,,
 Работа по перемещению проводника:
Работа по перемещению проводника:

 .
. Закон Био-Савара-Лапласа - определить напряженность магнитного поля, создаваемого элементом тока в любой точке С, расположенной от этого элемента на расстоянии r.
Закон Био-Савара-Лапласа - определить напряженность магнитного поля, создаваемого элементом тока в любой точке С, расположенной от этого элемента на расстоянии r.


 Закон Био-Савара-Лапласа поле кругового тока на его оси
Закон Био-Савара-Лапласа поле кругового тока на его оси

 Циркуляцией вектора B по заданному замкнутому контуру L называется следующий интеграл по этому контуру:
Циркуляцией вектора B по заданному замкнутому контуру L называется следующий интеграл по этому контуру: Теорема о циркуляции вектора B (закон полного магнитного поля в вакууме):циркуляция вектора B по произвольному замкнутому контуру равна произведению магнитной постоянной µ0 на алгебраическую сумму токов, охватываемых этим контуром.
Теорема о циркуляции вектора B (закон полного магнитного поля в вакууме):циркуляция вектора B по произвольному замкнутому контуру равна произведению магнитной постоянной µ0 на алгебраическую сумму токов, охватываемых этим контуром. Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов (токов намагниченности), охватываемых этим контуром, умноженной на магнитную постоянную:
Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов (токов намагниченности), охватываемых этим контуром, умноженной на магнитную постоянную:
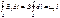
 Магнитное поле бесконечного проводника с током:
Магнитное поле бесконечного проводника с током: Магнитное поле соленоида:
Магнитное поле соленоида: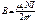

 Напряженность магнитного поля движущегося заряда также можно определить, используя закон Био – Савара – Лапласа. Таким образом Idl = jSdl = nqvSdl = nqdVv = Nqv, где dV – объем элемента проводника dl, N – полное число частиц в отрезке dl проводника.
Напряженность магнитного поля движущегося заряда также можно определить, используя закон Био – Савара – Лапласа. Таким образом Idl = jSdl = nqvSdl = nqdVv = Nqv, где dV – объем элемента проводника dl, N – полное число частиц в отрезке dl проводника. Силу действия магнитного поля на движущийся заряд можно найти исходя из закона Ампера. Пусть по проводнику длиной dl за промежуток времени dt проходит n элементарных зарядов величиной q, т.е. через проводник протекает ток, сила которого I=nq/dt.
Силу действия магнитного поля на движущийся заряд можно найти исходя из закона Ампера. Пусть по проводнику длиной dl за промежуток времени dt проходит n элементарных зарядов величиной q, т.е. через проводник протекает ток, сила которого I=nq/dt. Заряженная частица движется в магнитном поле вдоль линий магнитной индукции (угол a между векторами равен 0 или p). Сила Лоренца равна нулю. Магнитное поле на частицу не действует и она движется равномерно и прямолинейно.
Заряженная частица движется в магнитном поле вдоль линий магнитной индукции (угол a между векторами равен 0 или p). Сила Лоренца равна нулю. Магнитное поле на частицу не действует и она движется равномерно и прямолинейно. , Uн=RbjB, R-постоянная холла, b-ширина пластинки, j-плотность тока, B-магнитная индукция. Явление Холла наблюдается не только в металлах но и в полу проводниках, причем по знаку эффекта можно определить о принадлежности полупроводника к n или p типу.
, Uн=RbjB, R-постоянная холла, b-ширина пластинки, j-плотность тока, B-магнитная индукция. Явление Холла наблюдается не только в металлах но и в полу проводниках, причем по знаку эффекта можно определить о принадлежности полупроводника к n или p типу. Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина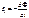 Закон Фарадея: ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром:
Закон Фарадея: ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром:

 При равномерном вращении рамки в однородном магнитном поле в ней возникает переменная ЭДС, изменяющаяся по гармоническому закону:
При равномерном вращении рамки в однородном магнитном поле в ней возникает переменная ЭДС, изменяющаяся по гармоническому закону: Действие генераторов основано на принципе электромагнитной индукции: в проводе, движущемся в магнитном поле, наводится электродвижущая сила (ЭДС). Действие электродвигателей основано на том, что на провод с током, помещенный в поперечное магнитное поле, действует сила. Все электрические машины вращательного типа делятся на машины постоянного и переменного тока.
Действие генераторов основано на принципе электромагнитной индукции: в проводе, движущемся в магнитном поле, наводится электродвижущая сила (ЭДС). Действие электродвигателей основано на том, что на провод с током, помещенный в поперечное магнитное поле, действует сила. Все электрические машины вращательного типа делятся на машины постоянного и переменного тока.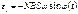

 Закон Ампера: на отрезок проводника длиной dl с током l помещенный в магнитное поле, действует сила
Закон Ампера: на отрезок проводника длиной dl с током l помещенный в магнитное поле, действует сила Индуктивность контура, соленоида, тороида.
Индуктивность контура, соленоида, тороида.
 Причем, статическая индуктивность -
Причем, статическая индуктивность - а динамическая индуктивность (при наличии ферромагнитной среды) -
а динамическая индуктивность (при наличии ферромагнитной среды) -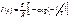 При замыкании цепи, получаем зависимость тока от времени:.
При замыкании цепи, получаем зависимость тока от времени:. При размыкании цепи, источник тока отключается от цепи. Поскольку ток в цепи определяется в основном ЭДС самоиндукции, ток в цепи равен току до момента отключения источника тока. Имеем следующую зависимость тока от времени.
При размыкании цепи, источник тока отключается от цепи. Поскольку ток в цепи определяется в основном ЭДС самоиндукции, ток в цепи равен току до момента отключения источника тока. Имеем следующую зависимость тока от времени. Энергия и плотность энергии магнитного поля.
Энергия и плотность энергии магнитного поля.

 Энергия, запасаемой в индуктивном элементе цепи, т.е. энергией магнитного поля или эквивалентной ей работой, затрачиваемой на увеличение сцепленного с контуром магнитного поля.
Энергия, запасаемой в индуктивном элементе цепи, т.е. энергией магнитного поля или эквивалентной ей работой, затрачиваемой на увеличение сцепленного с контуром магнитного поля.


