
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование дифференциального уравнения упругой линииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для того, чтобы получить аналитические выражения для прогибов и углов поворота, необходимо найти решение дифференциального уравнения (5.20). Правая часть уравнения является известной функцией для каждой конкретной балки с конкретным загружением. Интегрируя его один раз, получим:
Это выражение определяет закон изменения углов поворота сечений балки. После повторного интегрирования найдем уравнение оси балки
Постоянные интегрирования С и D находятся из граничных условий. Уравнения (5.20) записываются для каждого участка балки и интегрируются. При большом числе участков определение const Один из таких методов сводится к уравниванию однотипных const интегрирования, для чего при составлении аналитических выражений изгибающих моментов
Метод уравнивания произвольных постоянных (метод Клебша) Равенство между собой произвольных постоянных ( 1) Отсчет координат 2) Все составляющие выражения 3) Сосредоточенные моменты 4) Интегрирование дифференциальных уравнений надо вести без раскрытия скобок. Поясним выполнение перечисленных условий на примере: Пример 5.3: Дано: На рис. 5.11 сплошными линиями и перечеркнутыми показаны нагрузки
Рис.5.11
1) Из уравнений равновесия всей балки при заданных нагрузках находим все опорные реакции: 2) Строим эпюру Для балки подберем стандартный двутавр: Из условия прочности балки (5.17) находим
Из таблиц сортамента двутавров видно, что
Итак, №33 не подходит балке даже с учетом перегрузки. Проверяем №36:
Проверяем №36 по условию прочности (5.18), подставляя данные из сортамента:
Итак, окончательно для балки выбираем двутавр №36, который отвечает всем условиям прочности. Для определения деформации балки, т.е. I участок I Здесь в формуле а) первый минус – т.к. левая часть, второй минус – т.к. он стоит в (5.20) II участок II Здесь слагаемое с III участок III Все условия метода Клебша выполнены, поэтому должно быть: 1) Сечение А, опора, т.е. при
2) Сечение В, опора, т.е. при
Решаем уравнения (5) и (6), найдем
По формулам в) и с) на каждом участке балки вычислим
По этим данным строим эпюру
Проверка балок на жесткость Из условий нормальной работы конструкций часто ограничивают максимальные прогибы балок. Обычно вводят следующие ограничения: допускаемые прогибы пролета балки длиной Условия жесткости балки: – в пролете – в консолях Проверим балку рассматриваемого примера. Из рис. 5.11 или таблицы находим левая консоль:
Условие жесткости консоли выполняется. пролет:
Итак: Двутавр №36 отвечает всем требованиям к прочности и жесткости рассматриваемой балки. Если жесткость где-то не выполняется, берут следующий номер двутавра и проверяют его на жесткость. Для определения деформаций балок разработаны и другие методы, например: метод начальных параметров – достаточно близок к вышеизложенному методу Клебша, излагается во многих учебниках по Сопротивлению материалов. Метод Мора – позволяет довольно просто определять деформации отдельных сечений балки (метод не аналитический). Этот метод подробно рассмотрен в разделе 14, где и приводится пример 14.3 расчета балки по методу Мора.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 1524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.10.139 (0.007 с.) |

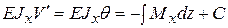 .
.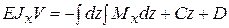 .
.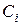 и
и 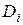 осложняется, т.к. приходится решать большое число совместных алгебраических уравнений, из которых они вычисляются. Поэтому для таких балок были разработаны другие методы.
осложняется, т.к. приходится решать большое число совместных алгебраических уравнений, из которых они вычисляются. Поэтому для таких балок были разработаны другие методы. по участкам балки необходимо соблюдать ряд условий.
по участкам балки необходимо соблюдать ряд условий.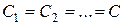 и
и 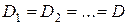 ) при большом числе участков балки возможно при соблюдении следующих условий:
) при большом числе участков балки возможно при соблюдении следующих условий: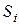 всех участков должен вестись от одного конца балки.
всех участков должен вестись от одного конца балки.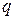 , не идущая до конца балки, то ее надо продлить до конца балки, добавив на этих же участках такую же распределенную нагрузку с противоположным знаком.
, не идущая до конца балки, то ее надо продлить до конца балки, добавив на этих же участках такую же распределенную нагрузку с противоположным знаком.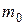 вводятся в виде
вводятся в виде 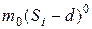 , где
, где 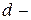 расстояние от начала балки до сечения, где приложены
расстояние от начала балки до сечения, где приложены  1,5м;
1,5м;  4,5м;
4,5м;  4м;
4м;  20кН;
20кН; 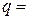 45кН/м;
45кН/м;  20кНм;
20кНм; 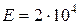 кН/см2;
кН/см2;  =16кН/см2;
=16кН/см2;  =10кН/см2; (рис.5.11).
=10кН/см2; (рис.5.11).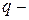 заданные, а пунктиром показаны добавки нагрузок
заданные, а пунктиром показаны добавки нагрузок 
 -154,12кН;
-154,12кН;  84,12кН;
84,12кН;  .
. и эпюру
и эпюру 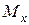 , из которых находим
, из которых находим 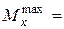 -105,68кНм и
-105,68кНм и 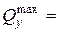 -106,62кН.
-106,62кН.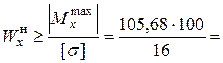 660,5см2.
660,5см2.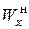 лежит между: №33
лежит между: №33 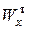 =597см3 и №36
=597см3 и №36 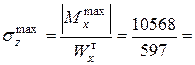 17,7кН/см2.
17,7кН/см2.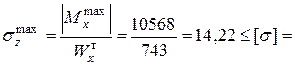 16кН/см2.
16кН/см2.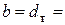 0,75см;
0,75см; 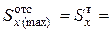 423см3;
423см3; 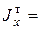 13380см4:
13380см4: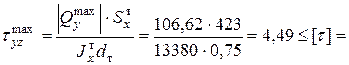 10кН/см2.
10кН/см2.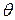 – углов поворота сечений и
– углов поворота сечений и 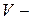 прогибов балки, с соблюдением условий метода Клебша для всех трех участков балки, записываем дифференциальные уравнения (5.20) и интегрируем их:
прогибов балки, с соблюдением условий метода Клебша для всех трех участков балки, записываем дифференциальные уравнения (5.20) и интегрируем их: левая часть (см. рис. 5.11)
левая часть (см. рис. 5.11)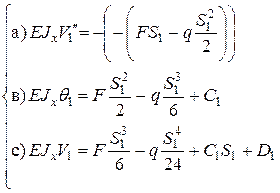
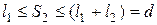 левая часть
левая часть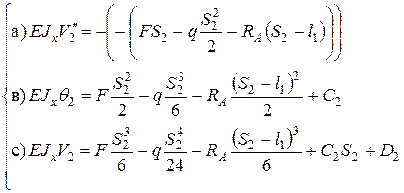
 интегрируется без раскрытия скобок согласно п.4 метода Клебша.
интегрируется без раскрытия скобок согласно п.4 метода Клебша.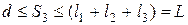 левая часть
левая часть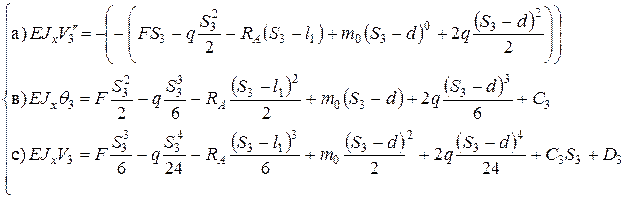
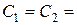
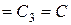 ,
, 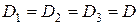 . Для определения const
. Для определения const 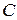 и
и 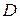 рассмотрим условия закрепления балки:
рассмотрим условия закрепления балки: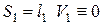 . Подставим это в формулу Iс), получим
. Подставим это в формулу Iс), получим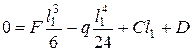 . (5)
. (5)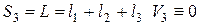 . Подставим это в формулу IIIс)
. Подставим это в формулу IIIс)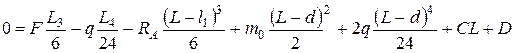 (6)
(6)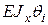 и
и 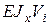 . Результаты вычислений сведем в таблицу
. Результаты вычислений сведем в таблицу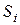 м
м
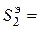 4,12
4,12
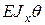 и эпюру
и эпюру 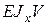 . Из эпюры
. Из эпюры 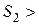 4м на эпюре
4м на эпюре 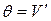 в сечении, где
в сечении, где 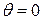 величина
величина 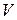 имеет экстремум. Найдем его. Расчеты показали, что при
имеет экстремум. Найдем его. Расчеты показали, что при 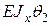 =0,47, т.е. близка к нулю. В этом сечении балки
=0,47, т.е. близка к нулю. В этом сечении балки 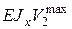 = – 302,2кНм3. С учетом этого строим окончательные эпюры на рис. 5.11. (По аналогии с
= – 302,2кНм3. С учетом этого строим окончательные эпюры на рис. 5.11. (По аналогии с 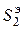 надо найти
надо найти 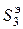 (на III участке при
(на III участке при 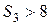 м) и вычислить
м) и вычислить 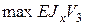 ).
).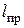
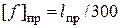 , а для консолей длиной
, а для консолей длиной 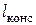
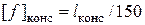 , или эти данные берут из справочников.
, или эти данные берут из справочников.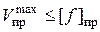
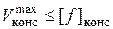
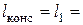 1,5м,
1,5м, 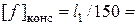 1см,
1см, 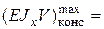 =258,8кНм3,
=258,8кНм3, 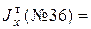 13380см4,
13380см4,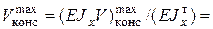
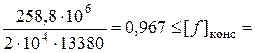 1см.
1см.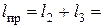 8,5м,
8,5м, 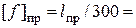 2,83см,
2,83см,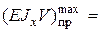 =302,2кНм3
=302,2кНм3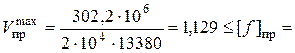 2,83см.
2,83см.


