
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Касательные напряжения в двутавровом сеченииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для стенки, вследствие малой ее ширины (
где: Подставляем
Рис.5.10
1) 2) 3) По этим точкам строим нижнюю часть эпюры Полка двутавра широкая и малой высоты и допущения Журавского для нее несправедливы и, следовательно, пользоваться (5.15) нельзя. В консолях полок возникают горизонтальные
Определение На верхней левой консоли полки проведем сечение на расстоянии
где
Видно, что 1) 2) Аналогичный закон изменения Направления
Условия прочности при поперечном изгибе. Подбор сечений
Расчет балок на прочность обычно ведется по наибольшим нормальным напряжениям, возникающим в их поперечных сечениях. Обозначая эти напряжения
I. Так как пластичные материалы одинаково сопротивляются как растяжению, так и сжатию, то для них
Отсюда определяется необходимая величина момента сопротивления
Размеры сечения (при выбранной форме) подбираются так, чтобы его момент сопротивления равнялся или был чуть больше требуемой величины. При проектировании балки прямоугольного сечения задаются соотношением сторон Для круглого сечения Подбор стальных балок прокатного профиля производится с помощью таблиц сортамента по величине В случае применения тонкостенных профилей типа двутавра или деревянных прямоугольных сечений балок (при значительной поперечной нагрузке
Подобранные сечения балки должны удовлетворять условиям прочности как по нормальным (5.17), так и по касательным напряжениям (5.18). Для деревянных балок расчет на прочность по Балки из хрупких материалов, плохо работающих на растяжение, изготавливают обычно с несимметричным относительно оси х сечением
Поэтому при проектировании таких сечений необходимо, чтобы
В железобетонных балках растянутая зона армируется металлом, чтобы увеличить
|
||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 878; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.140.108 (0.006 с.) |

 ), допущения Журавского справедливы и
), допущения Журавского справедливы и  в ней можно вычислить по (5.15). Для произвольного сечения на расстоянии «у» от оси х в пределах стенки, т.е.
в ней можно вычислить по (5.15). Для произвольного сечения на расстоянии «у» от оси х в пределах стенки, т.е.  , где
, где  , можно записать с учетом обозначений на рис. 5.10:
, можно записать с учетом обозначений на рис. 5.10: ,
, .
. в формулу (5.15), в которой заменяем размер «b» на размер «d» - ширина стенки, получим расчетную формулу, по которой можно построить эпюру
в формулу (5.15), в которой заменяем размер «b» на размер «d» - ширина стенки, получим расчетную формулу, по которой можно построить эпюру 


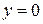 , находим
, находим  , подставим в (5.15) и вычислим
, подставим в (5.15) и вычислим  и откладываем ее в масштабе на эпюре
и откладываем ее в масштабе на эпюре  , аналогично вычислим
, аналогично вычислим  ;
; , находим
, находим 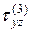 .
. . Если
. Если 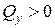 (вниз), то и
(вниз), то и  , которые можно найти по формуле
, которые можно найти по формуле . (5.16)
. (5.16) поясним с помощью рис. 5.10.
поясним с помощью рис. 5.10. и в этом сечении найдем
и в этом сечении найдем  . Тогда
. Тогда  ,
,  отсеченная площадь:
отсеченная площадь: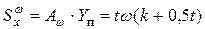 ,
, .
. (конец консоли),
(конец консоли), 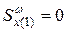 и из (5.16)
и из (5.16)  .
. , вычислим
, вычислим  и по (5.16)
и по (5.16)  .
. , направления
, направления  , получим условие прочности
, получим условие прочности .
. . Поэтому балки из пластичных материалов обычно имеют поперечные сечения, симметричные относительно своих нейтральных осей. Подбор сечения проводится из условия прочности действию наибольшего по абсолютной величине изгибающего момента
. Поэтому балки из пластичных материалов обычно имеют поперечные сечения, симметричные относительно своих нейтральных осей. Подбор сечения проводится из условия прочности действию наибольшего по абсолютной величине изгибающего момента . (5.17)
. (5.17) .
.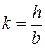 , тогда
, тогда  и
и  .
. , откуда
, откуда  .
.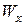 .
. ; (5.18)
; (5.18) и
и  берутся из нормативных документов для каждого материала.
берутся из нормативных документов для каждого материала. может иметь решающее значение, т.к. дерево плохо сопротивляется скалыванию вдоль волокон. Допускается перегрузка до 5% от
может иметь решающее значение, т.к. дерево плохо сопротивляется скалыванию вдоль волокон. Допускается перегрузка до 5% от 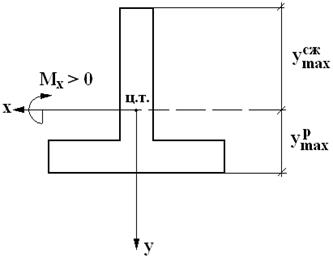
 Здесь учтено, что
Здесь учтено, что  отри-цательная величина и по модулю
отри-цательная величина и по модулю  .
.
 , а для равнопрочности желательно, чтобы
, а для равнопрочности желательно, чтобы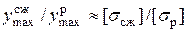 .
. .
.


