
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремальные напряжения. МоментСодержание книги
Поиск на нашем сайте
Сопротивления сечения Из формулы (5.12) видно, что экстремальные (max) напряжения (растягивающие (р) и сжимающие (сж)) будут в точках сечения балки, наиболее удаленных от нейтральной оси х:
Здесь
Обозначим
Тогда
Здесь знак напряжений для расчетов на прочность роли не имеет и определяется по физическому смыслу (в растянутой зоне сечения « Для прямоугольного сечения шириной b и высотой h:
Для круглого сечения радиуса
Для кольцевого сечения с
Значения Балки из хрупких материалов обычно изготавливают несимметричными относительно оси х. При этом для равнопрочности их желательно, чтобы расстояния до крайних точек сечения от оси х были пропорциональны допускаемым напряжениям на растяжение и сжатие. Нормальные и касательные напряжения в Прямоугольном сечении балки при поперечном Плоском изгибе
В отличие от чистого изгиба при поперечном изгибе в сечениях балки, наряду с нормальными напряжениями, появляются также и касательные напряжения, параллельные равнодействующей им силе
На основании закона парности касательных напряжений, последние возникают также и в продольных сечениях и вызывают сдвиги отдельных волокон относительно друг друга. Касательные напряжения в продольных сечениях обращаются в нуль на верхний и нижний поверхностях бруса и возрастают по какому-то закону к нейтральной оси. Следовательно, поперечные сечения балки, плоские до деформации, при поперечном изгибе от
ми не получат дополнительных деформаций по сравнению с деформациями от изгиба сечения. Поэтому в этом случае для определения нормальных напряжений можно пользоваться формулой (5.12), полученной для чистого изгиба 2) В этом случае абсолютные сдвиги неодинаковы и, следовательно, за счет сдвига продольные волокна получают дополнительные деформации и, значит, будет добавка в нормальных напряжениях. Однако теоретические и экспериментальные исследования показали, что влияние указанного эффекта на величину нормальных напряжений невелико и им обычно на практике пренебрегают. Таким образом, гипотеза плоских сечений условно распространяется также и на поперечный изгиб. Следовательно, при поперечном изгибе нормальные напряжения определяются по той же формуле чистого изгиба
Относительно распределения касательных напряжений 1. Касательные напряжения в любой точке сечения направлены параллельно поперечной силе 2. Касательные напряжения, действующие на одном и том же расстоянии от нейтральной оси х, равны между собой, т.е. по ширине сечения касательные напряжения распределяются равномерно. Исследования показывают, что оба допущения оказываются достаточно правильными для балок прямоугольного сечения, если высота балки больше ширины. С учетом этих допущений и была получена формула Журавского в виде*
Здесь: Выясним характер распределения
Рис.5.9
Найдем
Из рис. 5.9 видно:
Подставим
Видно, что 1) 2) 3) По этим точкам строим нижнюю половину эпюры
|
||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.203 (0.006 с.) |

 .
. и координаты
и координаты  надо подставлять со своими знаками, при этом автоматически получается знак
надо подставлять со своими знаками, при этом автоматически получается знак 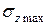 . Это важно для балок, изготовленных из хрупких материалов (чугун, бетон), которые хорошо работают на сжатие и плохо на растяжение. Балки из пластичных материалов (стали) одинаково сопротивляются растяжению и сжатию, поэтому обычно их поперечные сечения симметричны относительно оси х (двутавр), для них
. Это важно для балок, изготовленных из хрупких материалов (чугун, бетон), которые хорошо работают на сжатие и плохо на растяжение. Балки из пластичных материалов (стали) одинаково сопротивляются растяжению и сжатию, поэтому обычно их поперечные сечения симметричны относительно оси х (двутавр), для них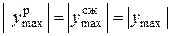 и
и  .
.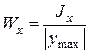 – момент сопротивления симметричного сечения. (5.13)
– момент сопротивления симметричного сечения. (5.13) . (5.14)
. (5.14) »).
»). .
.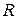
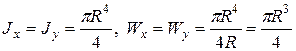 .
.

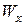 для стандартных двутавров и швеллеров приводятся в таблицах ГОСТа.
для стандартных двутавров и швеллеров приводятся в таблицах ГОСТа.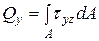 .
. , искривляются. Это искривление, в соответствии с характером изменения величины касательных напряжений, возрастает от краев балки к нейтральной оси (рис. 5.8). Следовательно, гипотеза плоских сечений при поперечном изгибе нарушается.
, искривляются. Это искривление, в соответствии с характером изменения величины касательных напряжений, возрастает от краев балки к нейтральной оси (рис. 5.8). Следовательно, гипотеза плоских сечений при поперечном изгибе нарушается.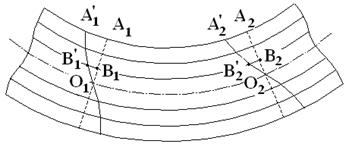 Рис.5.8
Рис.5.8
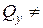 const, т.е.
const, т.е. 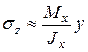 .
. Д.И.Журавским были сделаны следующие допущения:
Д.И.Журавским были сделаны следующие допущения: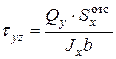 . (5.15)
. (5.15) ширина сечения, где определяются
ширина сечения, где определяются  статический момент относительно оси х отсеченной части сечения.
статический момент относительно оси х отсеченной части сечения. (вниз).
(вниз).
 * Вывод этой формулы приводится во многих учебниках по Сопротивлению материалов, например [1,4,11,22 и др.].
* Вывод этой формулы приводится во многих учебниках по Сопротивлению материалов, например [1,4,11,22 и др.]. (заштрихована на рис. 5.9). Расстояние от оси х до центра тяжести
(заштрихована на рис. 5.9). Расстояние от оси х до центра тяжести 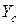 . Тогда
. Тогда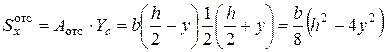 .
. .
. в формулу (5.15):
в формулу (5.15):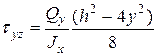 . (5.15а)
. (5.15а)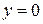 (точка на оси х)
(точка на оси х) 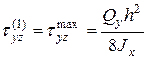 ;
;
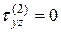 ;
;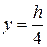
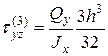 .
.


