
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение эпюр изгибающих моментов иСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Перерезывающих сил
Для расчетов на прочность необходимо отыскать опасное сечение балки, в котором действуют наибольшие ВСФ. Для этого необходимо знать закон изменения ВСФ в поперечных сечениях балки по ее длине, возникающих от действия на балку нагрузок. Этот закон можно выразить в виде аналитических зависимостей и изобразить с помощью специальных графиков, называемых эпюрами, которые в масштабе изображают значения функций Для определения этих эпюр определяют численные значения моментов и перерезывающих сил для ряда сечений и по ним строят соответствующие эпюры. На основании зависимостей, характеризуемых выражениями (5.2) и (5.3), легко определить значения Условимся: на эпюрах Рассмотрим несколько примеров, из которых можно усвоить технику построения эпюр Пример 5.1.
произвольно вверх. Опора А – шарнирно-неподвижная, в ней могут быть две реакции: 1) 2) Для определения
Откуда Реакция 3) Для определения
Откуда Обязательно надо сделать проверку реакций, составив еще одно уравнение статики, например, Итак: II. Построение эпюр внутренних силовых факторов. В соответствии с характером конструкции балки и нагрузки делим балку на три участка. Эпюры I участок длиной
т.е. эпюра
т.е. эпюра Посчитаем величины
Строим эпюры II участок длиной
Считаем:
III участок. Проводим сечение, видно, что проще рассмотреть правую отсеченную часть. В этом случае расстояние до сечения а) б) Считаем: Эпюра Экстремальные значения На эпюрах ставим знаки, размерность величин, штриховка перпендикулярна к оси бруса (вертикальная).
Проверка построенных эпюр Существует несколько способов проверки эпюр, в том числе с использованием зависимостей (5.4) и (5.5). Рассмотрим два самых простых способа: 1. Проверка эпюры Итак, во всех сечениях правило выполняется. 2. Проверка эпюры Итак, во всех сечениях правило выполняется. Наличие на эпюре Пример 5.2. Криволинейный брус радиуса Дано:
  
Рис.5.6 Опорные реакции в заделке Кроме
Учитывая, что мы рассматриваем левую отсеченную часть арки, по формулам (5.2), (5.3) и (5.7) получим:
Здесь
Выбираем масштабы для 1. Если на эпюре
Отсюда
2. Если на эпюре По (5.8в)
По (5.8а) и (5.8с) найдем при
Найденные экстремальные значения откладываем на эпюрах, и с их учетом строим окончательные эпюры
|
||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.241.191 (0.013 с.) |

 и
и  на протяжении всей балки.
на протяжении всей балки. Рис.5.5
Рис.5.5
 2кН,
2кН,  1кНм,
1кНм,  2кНм,
2кНм,  1м,
1м,  2м,
2м,  1,5м,
1,5м,  1кН/м (рис.5.5).
Решение задачи:
I. Начнем с определения опорных реакций: опора В – шарнирно-подвижная, в ней может возникнуть только вертикальная реакция
1кН/м (рис.5.5).
Решение задачи:
I. Начнем с определения опорных реакций: опора В – шарнирно-подвижная, в ней может возникнуть только вертикальная реакция  – направим ее
– направим ее
 горизонтальная и
горизонтальная и  – вертикальная, нарисуем их тоже произвольно. Для определения всех реакций составим три уравнения статики для всей балки:
– вертикальная, нарисуем их тоже произвольно. Для определения всех реакций составим три уравнения статики для всей балки: Откуда
Откуда 
 . Все внешние моменты, направленные против хода часовой стрелки, считаем положительными. Все погонные нагрузки
. Все внешние моменты, направленные против хода часовой стрелки, считаем положительными. Все погонные нагрузки  постоянные, поэтому их равнодействующие
постоянные, поэтому их равнодействующие  действуют в середине участков.
действуют в середине участков.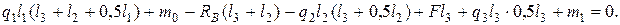
 1,75кН.
1,75кН. :
:
 , т.е. суммировать все нагрузки и найденные реакции на ось у:
, т.е. суммировать все нагрузки и найденные реакции на ось у:  . Получим 0 = 0.
. Получим 0 = 0. .
. . Проведем сечение в пределах участка. Видно, что проще рассмотреть левую отсеченную часть. Тогда сечение определим расстоянием
. Проведем сечение в пределах участка. Видно, что проще рассмотреть левую отсеченную часть. Тогда сечение определим расстоянием  от т. D.
от т. D.  (лев) – пределы изменения
(лев) – пределы изменения  ,
, ,
, .
. . Рассмотрим тоже левую часть
. Рассмотрим тоже левую часть  (лев):
(лев):

 Строим эпюры
Строим эпюры  будем отсчитывать от опоры А,
будем отсчитывать от опоры А,  (правая часть):
(правая часть): ;
;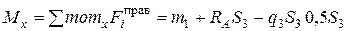 .
. .
. эпюра
эпюра  принимает экстремальное значение. Подставим в формулу а)
принимает экстремальное значение. Подставим в формулу а)  , отсюда
, отсюда  0,75 м. Подставим
0,75 м. Подставим  = 2,28 кНм. Это будет третьей точкой для построения эпюры
= 2,28 кНм. Это будет третьей точкой для построения эпюры  .
. 0,75кН вверх; сечение С, здесь скачок вниз от 0,75 до 2,75, т.е. на 2 кН, здесь действует
0,75кН вверх; сечение С, здесь скачок вниз от 0,75 до 2,75, т.е. на 2 кН, здесь действует 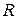 (арка)
(арка) 2м,
2м, 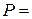 2кН,
2кН, 

 можно определить из обычных трех уравнений статики. По виду конструкции арки и ее нагрузки имеем только один участок. В произвольном месте арки делаем разрез (сечение) в т. D. Очевидно, что проще рассмотреть ту часть арки
можно определить из обычных трех уравнений статики. По виду конструкции арки и ее нагрузки имеем только один участок. В произвольном месте арки делаем разрез (сечение) в т. D. Очевидно, что проще рассмотреть ту часть арки  , где приложены нагрузки, тогда не надо определять все реакции опор
, где приложены нагрузки, тогда не надо определять все реакции опор 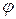 (т. D надо выбрать так на рис. 5.6, чтобы угол
(т. D надо выбрать так на рис. 5.6, чтобы угол  так, чтобы ось
так, чтобы ось  была направлена по касательной к арке в т. D,а ось
была направлена по касательной к арке в т. D,а ось  по радиусу. Здесь
по радиусу. Здесь  , т.е. в пределах всей арки рассматривается левая часть арки от разреза. Силы
, т.е. в пределах всей арки рассматривается левая часть арки от разреза. Силы  и
и  разложим на составляющие по осям
разложим на составляющие по осям 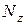 – внутренние продольные силы, которые определяются по формулам, аналогичным (5.2) и (5.3), полученным в разделе 1.
– внутренние продольные силы, которые определяются по формулам, аналогичным (5.2) и (5.3), полученным в разделе 1. . (5.7)
. (5.7) (5.8)
(5.8) и
и  плечи у сил
плечи у сил 
 и откладываем полученные значения с учетом знаков: положительные – внутрь, т.е. вдоль оси
и откладываем полученные значения с учетом знаков: положительные – внутрь, т.е. вдоль оси  , где
, где  . Далее в (5.8в) подставим
. Далее в (5.8в) подставим  . На нашей эпюре
. На нашей эпюре  .
. и угол
и угол 
 = – 4,47кН.
= – 4,47кН. , где
, где  ,
, и угол
и угол  .
. = – 4,47кН;
= – 4,47кН; = – 14,94кНм.
= – 14,94кНм. и
и 


