
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютное, атмосферное, избыточное давления и давление вакуума.Содержание книги
Поиск на нашем сайте
Понятие ж, виды. Жидкость – это физ-е тело, обладающее свойствами текучести, т.е способностью изменять свою форму под действием сколь угодно малых сил. Св-во текучести обусловлено тепловым перемещением молекул и проявляется в малой сопротивляемости деформации сдвига, т.е в малой упругости формы. Жидкость не имеет форм. Термин ж явл-ся собират-ым, он использ-ся для обозначения жидкости, газов. Принято ж разделять на капельные(1) и газообразные(2) ж. Капельные: вода (малые объемы), керосин, бензин, минер-е масла. Газообразная: воздух, газы, пары, смеси газов и паров. Некоторые св-ва: (1): Малая сжимаемость, капельные ж занимают часть представленного объема, образуя поверхность раздела ж, газ, к-я наз-ся свободной поверхностью. (2): легко сжимаются. Капельные ж по характеру молекулярных движений численному значению молекулярных сил занимают промежуточное положение между твердыми телами и газами, поэтому они обладают св-ми, характерными как для твердых тел, так и для газов. Рис.
Модель жидкости. В гидравлике при изучении з-ов равновесия и движения реальная ж заменяется ее моделью. Требования: Модель должна отражать существенные, решаемые в рамках данной задачи св-ва ж, быть достаточно простой, наглядной и допускать применения мат. Методов анализа, - иначе польза будет мала. В гидравлике использ-ся модель ж, в основе к-ой лежит гипотеза сплошности высказанная франц ученым в 1841 Даламбером. Согласно гипотезе ж состоит из бесконечного множ-ва элементарных объемов, к-е наз-ся жидкими частицами, они примыкают друг к другу и заполняют без промежутков все предоставленное пространству. Параметры ж в пределах частицы, такие как скорость, давление, плотность, вязкость и т.д измен-ся на бесконечно малую величину. Ж-е частицы взаимод-т друг с другом и ограничиваюие поверхностями перемещ-ся и деформируются, при этом их объем и форма изменяется, однако масса каждой из частиц остается неизменной. Предполаг-ся, что к жидким частицам применимы з-ны механики тв тела, что явл-ся мостом. Данная гипотеза позволяет представить ж сложной средой, масса к-й непрерывно распределена по объему. В силу этого и все остальные параметры явл-ся непрерывными по объему и представляет собой дифференцируемые ф-ии координат точки и времени. Она значительно упрощает исследование равновесия и движ-е ж, позволяя применять для их описания дифференциальное исчисление. В любой науке столько истины, сколько в ней матем-ки. В гидравлике ж замен-ся ее моделью.
Плотность ж. Интенсивность распределения массы по объему характеризует величина, к-ю наз-ют плотностью. Плотность явл-ся основной харак-ой жид-ти. Понятие плотности ввел Ньютон. Плотность (ρ) – это отношение массы ж к объему, к-й она занимает. ρ= Плотность ж измер-ся ареометрами и пикнометрами.
Основные св-ва ж. Объемные св-ва ж. Объем ж – явл-ся функцией от давления и темпер-ры V=V(p,t) Пусть при р и t получим приращение Δр иΔt относит-но своих начальных значений. Необходимо восполь-ся ф-ой Тейлора: V(p+Δp; t+Δt)= V(p,T) - - Коэфициент, входящий в соотнош-е (1) (стоящий перед Δр в (1)) наз-ся изотермическим коф-ом объемного сжатия (β) βр= Коэф-т, стоящий в выражении (1) перед Δt именуетсяизобарным коэф-ом объемного расширения βt. βt=- Будем рассматривать 2 характерных случая. 1-й случай: Предположим, что сжатие ж происходит при постоянной темпер-ре Δt=0—(5):
5.Вязкость ж. Вязкость – это св-во ж оказывать сопротивление относительному сдвигу слоев. Вязкость проявляется в том, что при относ-ом перемещении слоев на поверхности их соприкосновения возникают силы сопротивления сдвигу, к-е наз-ся силами внутр-го трения или силами вязкости. Эти силы явл-ся следствием межмолекулярных связей между соприкасающимися слоями и существуют только в движущейся ж. Рис. Скорсть слоев увелич-ся по мере удаления от тв стенки. Скорости слоев разные. Гипотеза Ньютона: 1686г: при слоистом течении ж, силы внутр трения между слоями пропорциональны площади соприкосновения и градиенту скорости. Т-сила вязкого трения. Т=±µS Кроме динамической вязкости в гидравлике используют понятие кинемат-ой вязкости υ= Вязкость ж. измер-ся с помощью вискозиметра (В) Они подраздел-ся на капиллярные В, В истчения, шариковые В, ротационные и ультразвуковые.
6.Растворимость газов в ж. Парообразование. Кипение. Кавитация. Все ж в опред-ой степени поглощают и растворяют газы. Кол-во поглощенного газа зависит от давления. Чем больше давление, тем больше объем газа раствор-ся в ж. Понижение давления в какой-либо точке гидросистемы влечет за собой выделение в этом месте мельчайших пузырьков и образование пены. Это приводит к уменьшению плотности ж, увеличению сжимаемости, нарушению сплошности потока. Пример насыщения ж газом: газировка, кисонная болезнь. Парообразование. Капельные ж при опред-х давлениях и температуре переходят в газообразное состояние. Этот процесс наз-ся парообразованием. Обратный процесс – процесс перехода из газообразного состояния в жидкое наз-ся – конденсацией. В замкнутом простр-ве указанные переходы могут существовать одновременно. Это состояние наз-ся насыщенным паром. Давление, соответствующее этому состоянию наз-ся давлением насыщенного пара (рнп), к-е зависит от рода ж и темпер-ры. С увеличением темпер-ры давление насыщенного пара растет. Кипение ж. Кипение – процесс интенсивного парообразования внутри ж. При этом образ-ся пузырьки и полости с паром, к-е всплывают и выходят через свободные поверхности ж. Кипение возникает при р=рнп. При кипении р в ж не м.б больше рнп. Температура при к-ой р=рнп наз-ся температурой кипения. Конденсация паров происходит при р>рнп. Кавитация – явление местного выкипания ж с последующей конденсацией ее паров. Давление в ж сначала уменьш-ся, а затем происходит кипение, образ-е пузырьков, а потом р увелич-ся. Смыкание пузырьков и полостей паров сопровождается характерным шумом, местным повышением давления до сотен и температуры до 1000-1500 градусов. Пути борьбы: испоз-е кавитационно-стойкихматер-ов (резина, бутан). Кавитация в послед-м время использ-ся с пользой для дела: -очистка внутр поверхностей емкостей, -обогревательные устройства (шумный)
Силы, действующие в ж. Гидростатика – раздел гидравлики, изучающий з-ны равновесия ж. Равновесие ж – состояние покоя ж относительно водяного тела отсчета. Ж наход-ся в равновесии благодаря действующим на нее силам. Сила – это мера взаимодействия тел (ж, огранич-е поверх-ти). В гидравлике рассм-ся внутренние и внешние силы. Внешние – мера взаимод-я ж с ограничивающими поверхностями и др телами. Внутр-е силы – результат взаимод-я жидких частиц между собой. Подвижность жидких частиц не позволяет ж воспринимать сосредоточенные силы, поэтому в ж действуют только распределенные силы, к-е можно разделить на 2 группы: Поверхностные силы: к ним относ-ся силы непрерывно распределенные по поверхности ограничивающей объем ж илинамеченной внутри ж. Намеченной – это мысленно проведенной. Эти силы явл-ся результатом непосредственного взаимодействия жидких частиц между собой и жидких частиц с ограничивающими поверхностями. Величина этих сил пропорциональна площади поверхности по к-ой они действуют. Поверхностные силы могут быть разложены на 2 составляющие: нормальной к поверхности и касательной к поверхности. Нормальная составляющая – это сила давления. Касательная составляющая – сила поверхностного натяжения, сила внутр-го трения. Массовые силы – это силы, дествующие на каждую жидкую частицу и непрерывно распределенные по всему объему ж. Они явл-ся результатом полевого взаимодействия, непосредственного контакта нет. Их величина пропорциональна массе. К ним относ-ся: сила тяжести и сила инерции. Единичная поверхностная сила – это поверхностная сила, отнесенная к единице площади. Она характер-ет интенсивность распределения повер-ых сил. Физически – напряжения, нормальные или касательные в зависимости от напр-я сил. Нормальные напряжения при сжатии наз-ся давлением. Капельные ж. не оказывают сопротивление растяжению. Ж. не оказыв-т сопрот-е растяжению, в ней невозможны напр-я растяжению. Единичная массовая сила – это массовая сила, отнесенная к единице массы. Физич-й смысл – ускорение жидкой частицы. 8.Гидростатическое давление и его св-ва. Рис. Вокруг точки А, наход-ся в покоящейся ж выделим малый объем ΔV. ΔТ=µS Давление – это мера интенсивности внутр-х поверхностных сил в ж, к-е вызваны поверхностными внешними и массовыми внеш силами. Давление в покоящейся ж наз-ся гидростатическим. Из соотношения (1) следует, что направ-е давления р совпадает снаправ-ем силы ΔF, т.к ΔS- это скаляр. Единца измерения давления в СИ – Па, 1Па= 1Н/м2 На практике применяют и другие системные и внесистемные единицы измер-я р: бар, мм РТ ст, мм вод ст, техническая атмосфера (ат), физическая атмосфера (а). Численно Паскаль связан с указанными ед-ми след-им образом: 1бар=105Па, 1мм РТ ст. 133,3 Па, 1мм вод ст=9,81Па, 1а.т=0,981* 105Па= 98,1кПа, 1а=1,013*105=101,3кПа Св-ва гидростатического давления: 1. На внешней поверх-ти жидкости ГСД направлено по нормали внутрь объема ж. 2. В любой точке внутри ж ГСД давление по всем направлениям одинаково, т.е не зависит от наклона площадки ΔS по к-ой оно действует. Физически эти св-ва обусловлены тем, что покоющаяся ж не передает касательные и растягивающие силы, а воспринимает только равномерные всесторонне сжатие, т.е любая жидкая частица сжата со всех сторон одинаково. Как правило измеряют избыточное давление, к-е измер-ся манометрами: механические и жидкостные.
Всасывание ж поршнем. Рассм-м цилиндр с поршнем, погруженный в сосуд с жидкостью. Рис. Р=ра-ρgh, величение h влечет за собой уменьшение давления, рнп=ра-ρghпр - - hпр=(ра-рнп)/ρg Перемещение поршня вверх приводит к увеличению объема поршневой полости цилиндра. В рез-те уменьш-ся давление в жид-ти под поршнем. Под действием разности давлений (ра-р) жид-ть подним-ся за поршнем. Подъем поршня влечет увеличение Vоп - - уменьшение давления - -ра-р - -подъем жидкости.
З-н Архимеда. Рассмотрим однородное тело произвольной формы, полностью погруженное в жидкость. Пусть объем этого тела √т. У однородного тела геометр-й центр и центр тяжести совпадают ГЦ=ЦТ. Рис. Поверхность тела разобьем на 2 части: верхнюю КЕС и нижнюю КДС. Будем рассматривать их как крив-е стенки, к-е испытывают давление от вышележащих слоев жид-ти. Гориз-е составляющие сил, действующие на эти пов-ти уравновешив-ся. Надо определить вертик-ю силу, к-е действуют на тело. Для этого воспольз-ся понятием тела давления. Для верх поверх-ти тело давления АВСЕКА, объемом √В, явл-ся положит-ым. Вертик-я составляющая силы проходит через центр тяжести направлена сверху вниз. FВ=ρg√В. Для нижн пов-ти тело давления АВСВКА, объемом √н, явл-ся фиктивным или отриц-ым, вертик-я сила = Fн=ρп√н=ρg(√т+√В) сила направлена снизу вверх. Fн>FВ, FA=Fн-FВ=ρgVт, где FА- сила Архимеда, она приложена в центре тяжести тела и точка приложения этой силы наз-ся центром водоизмещения. На тело, погруженное в покоящуюся ж действует выталкивающая сила, направ-я вертик-но вверх и равная весу ж, вытесненной телом – з-н Архимеда. Тело имеет вес: 3случая: 1. FA=G, тело плавает, наход-ся в равновесии, 2. FA<G тело тонет, 3. FA>G тело всплывает
Виды движения ж. Кинематика ж – раздел гидравлики, кй изучает движ-е ж без учета причин, к-е его вызывают (а вызывают движ-е массовые силы). Рассм-м движ-е ж в простр-ве, ограниченном направляющими поверхностями. С этим простр-ом свяжем прямоуг-ю систему координат 0xyz. Рис. Скорость ж в заданной точке пространства наз-ся местной скоростью. Она явл-ся непрерывной функцией координат точки и времени. V=V(x,y,z,t)={Vx(x,y,z,t),Vy(x,y,z,t), Vz(x,y,z,t)}= {Vx, Vy, Vz}. Задача кинематики ж заключ-ся в определении скоростей движ-я в различных точках пространств, т.е в нахождении поля местных скоростей. Классификация видов движения: По характеру изменения поля скоростей во времени движ-я ж подраздел-ся на 1. неустановив-е или нестационарное движ-е ж с изменяющимся во времени местными скоростями По характеру изменения поля скоростей в пространстве установившееся движ-е ж м.б: неравномрным, равномерным, плавноизменяющимся. 1. При неравномерном движ-ии местные скорости мен-ся в простр-ве по вел-не и направ-ю. N: установив-сядвиж-е ж в местах деформации потока. 2. При равномерном движ-ии местная скорость неизменна во всех точках пространства. N: установ-ся движ-е ж в прямолин-м цилиндрическом трубопроводе. 3. Плавно – изменяющееся движ-е хар-ся плавным изменением поля скорости в пространстве. К нему применимы законы равномерного движ-я. N: плавный поворот.
Потоки ж. Потоком наз-ют движущуюся массу ж, ограниченную направляющими поверхностями. По харак-ру и сочетанию ограниченных поверхностей различают безнапорные, напорные потоки и гидравлические струи. 1. Безнапорный поток. Примером может служить поток ж в канале или трубе, работающей в неполном сеч-ии. Безнапорный поток – поток, ограниченный частично твердой и частично свободной поверхностями. Рис. 2. Напорный поток – это поток, ограниченный твердыми направляющими поверх-ми. N: поток ж в трубе, работающей полным сечением. Рис. 3. Гидравлическая струя – это поток, ограниченный только ж или толко газовой средой. N: струя из пожарного трансполта. Рис. Струя, огранич-я газовой средой наз-ся свободной. Струя, огранич-й ж наз-ся затопленной. В рамках струйной модели ж поток рассмат-ся как бесконечная совокупность элементар-х струек, к-е не перемещ-ся, а при разных скоростях скользят относ-но друг друга.
Уравнение неразрывности. В соответствии со струйной моделью ж поток можно представить бесконечной совокупностью этих струек. Элемен-е струйки явл-ся непроницаемыми, а жид-ть сплошной и несжимаемой, поятому объемный расход вдоль потока есть вел-на постоянная: Q=const вдоль потока, VсрS=const вдольпотока (1). Соотношение (1) наз-ся уравнением неразрывности или урав-ем постоянства расхода вдоль потока. Оно явл-ся математ-им выражением принципа сплошности и з-на сохранения массы. Из последнего соотношения следует, что с увеличением площадки живого сечения средняя скорость в нем уменьш-ся и наоборот с уменьшением площади сечения скорость увелич-ся. Рис с примером. Скорсти в сеч-ях обратно пропорциональны их площадям.
Режимы движ-я ж. При движ-ии ж в трубах и каналах возможны 2 принцип-но разных режима движ-я: ламинарный и турбулентный. Основной отличный признак этих режимов – характер характер движ-я отдел-х частиц и объемов ж. 1. Ламинарный режим движ-я – это течение без перемешивания частиц, без пульсации скоростей и давлений. Движение упорядоченное, параллельно струйное. Ламинарный в переводе с лат слоистый. При ламинар-ом движ-ии эпюра распред-я местных скоростей по сечению потока в круглой трубе имеет вид парабалоида вращения. Рис. Средняя скорость – это фиктивная скорость, при к-ой расход жидкостей через сечение = действительному расходу. VсрS= 1873г Рейнольдс. Было установлено, что определить режим движения ж можно с помощью безразмерного комплекса, к-ый в последствии был назван числом Рейнольдса Re=Vсрd/υ, Vср- скорость средняя, d- диаметр трубы (внутренний), υ- кинематич-я вязкость. Число Рейнольдса, при котором происходит смена режимов движ-я наз-ся критическим. Существует 2 значения критического числа Рейнольдса: 1. Верхние значения критического числа Рейгольдса соответствует переходу ламинарного режима в турбулентный. 2. Нижнее знач-е крит-го числа Рейнольдса соответствует переходу турбул-го режима к ламинарному. Рис. Reкр=Reкр.н Считается, если число Рейнольдса будет меньше крит-го знач-я числа Рейнольдса, то режим движ-я ламинарный, если больше или равно, то режим турбулентный. Reкр=2320 (для трубы круглого сечения). Скорость, соответствующая крит-му числу Рейнольдса наз критической Vкр=υReкр/d
Характеристика труб-да. Рассмотрим простой трубопровод произвольно расположенный в пространстве, он состоит из прямых участков одинакового диаметра, между которыми включены местные сопротивления (поворот, вентиль, фильтр, обратный клапон и т.д.) рис. d=const, Vср=Q/S=4Q/πd2. Уравнение Бернулли для выделенных сечений: Н1=Н2+h1-2 - разность полных напоров в начальном и конечном сечении трубопровода равна суммарным потерям на трубопроводе. Где Н1 и Н2 – полные напоры в соотствующих сеч-х. h1-2 – суммарные потери напора на трубопроводе. В соответствии с принципом наложения (суперпозиции) суммарные потери напора на простом трубопроводе склад-ся из потерь на прямолинейных участках и потерь на местных сопротивлениях h=h1-2=∑hтр i+∑hм I (1) Подставим соотношение (1) в формулы Дарси – Вейсбаха для потерь на местных сопротивлениях: h=∑λi Зависимость суммарных потерь напора на трубопроводе от расхода жидкости через него h=h(Q)=R(Q)Q2 назыв-ся характеристикой трубопровода, а величина R(Q) – гидравлическим сопротивлениемтрубопровода или просто сопротивление трубопровода. Характеристикой трубопровода, полученная экспериментальным путем выглядит след-им образом: рис. В этом случае говорят о квадратичном законе сопротивления, ему соответствует квадратичная харак-ка трубопровода.
Способы подачи ж. Пермещение ж по трубопроводу происходит за счет мех-ой энергии, к-я сообщается разностью полных напоров в начале и конце трубопровода. Ж движ-ся от сеч-я с большим полным напором к сеч-ю с меньшим полным напором. Рис. При установившемся движении запас полного напора Н1-Н2, т.е удельная энергия, сообщенная жидкости в общем случае расхоуется: 1. На подъем ж. на выс z2-z1, 2. На преодоление разности давлений в конечном и начальном сечениях трубопроводов. 3. На преодоление гидравлических сопротивлений. Запас или перепад напоров Н1-Н2 может быть создан след-ми способами: 1. За счет разности уровней жидкости в начале и конце трубопровода. В этом случае говорят о подаче ж самотеком. 2. Благодаря разности давлений в емкостях, соед-ых трубопроводом. Это подача вытеснением или выдавливанием. 3. С помощью насоса (насосная подача). Возможны различные комбинации указанных способов.
Истечение под уровень. На практике часто приходится иметь дело с истечением ж в простр-во заполнено жидкостью. Такой случай истечения наз-ся истечением под уровень или истечением под затопленное отверстие. 2 рис-ка.
Т.о имеет те же расчетные соотношения, что и при истечении струи в воздух. Отличие состоит в том, что напор истечения Н представляет собой разность потенц-ых (гидростатич-х) напорах по обе стороны отверстия в стенке.
Понятие ж, виды. Жидкость – это физ-е тело, обладающее свойствами текучести, т.е способностью изменять свою форму под действием сколь угодно малых сил. Св-во текучести обусловлено тепловым перемещением молекул и проявляется в малой сопротивляемости деформации сдвига, т.е в малой упругости формы. Жидкость не имеет форм. Термин ж явл-ся собират-ым, он использ-ся для обозначения жидкости, газов. Принято ж разделять на капельные(1) и газообразные(2) ж. Капельные: вода (малые объемы), керосин, бензин, минер-е масла. Газообразная: воздух, газы, пары, смеси газов и паров. Некоторые св-ва: (1): Малая сжимаемость, капельные ж занимают часть представленного объема, образуя поверхность раздела ж, газ, к-я наз-ся свободной поверхностью. (2): легко сжимаются. Капельные ж по характеру молекулярных движений численному значению молекулярных сил занимают промежуточное положение между твердыми телами и газами, поэтому они обладают св-ми, характерными как для твердых тел, так и для газов. Рис.
Модель жидкости. В гидравлике при изучении з-ов равновесия и движения реальная ж заменяется ее моделью. Требования: Модель должна отражать существенные, решаемые в рамках данной задачи св-ва ж, быть достаточно простой, наглядной и допускать применения мат. Методов анализа, - иначе польза будет мала. В гидравлике использ-ся модель ж, в основе к-ой лежит гипотеза сплошности высказанная франц ученым в 1841 Даламбером. Согласно гипотезе ж состоит из бесконечного множ-ва элементарных объемов, к-е наз-ся жидкими частицами, они примыкают друг к другу и заполняют без промежутков все предоставленное пространству. Параметры ж в пределах частицы, такие как скорость, давление, плотность, вязкость и т.д измен-ся на бесконечно малую величину. Ж-е частицы взаимод-т друг с другом и ограничиваюие поверхностями перемещ-ся и деформируются, при этом их объем и форма изменяется, однако масса каждой из частиц остается неизменной. Предполаг-ся, что к жидким частицам применимы з-ны механики тв тела, что явл-ся мостом. Данная гипотеза позволяет представить ж сложной средой, масса к-й непрерывно распределена по объему. В силу этого и все остальные параметры явл-ся непрерывными по объему и представляет собой дифференцируемые ф-ии координат точки и времени. Она значительно упрощает исследование равновесия и движ-е ж, позволяя применять для их описания дифференциальное исчисление. В любой науке столько истины, сколько в ней матем-ки. В гидравлике ж замен-ся ее моделью.
Плотность ж. Интенсивность распределения массы по объему характеризует величина, к-ю наз-ют плотностью. Плотность явл-ся основной харак-ой жид-ти. Понятие плотности ввел Ньютон. Плотность (ρ) – это отношение массы ж к объему, к-й она занимает. ρ= Плотность ж измер-ся ареометрами и пикнометрами.
Основные св-ва ж. Объемные св-ва ж. Объем ж – явл-ся функцией от давления и темпер-ры V=V(p,t) Пусть при р и t получим приращение Δр иΔt относит-но своих начальных значений. Необходимо восполь-ся ф-ой Тейлора: V(p+Δp; t+Δt)= V(p,T) - - Коэфициент, входящий в соотнош-е (1) (стоящий перед Δр в (1)) наз-ся изотермическим коф-ом объемного сжатия (β) βр= Коэф-т, стоящий в выражении (1) перед Δt именуетсяизобарным коэф-ом объемного расширения βt. βt=- Будем рассматривать 2 характерных случая. 1-й случай: Предположим, что сжатие ж происходит при постоянной темпер-ре Δt=0—(5):
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.185.207 (0.014 с.) |

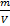 (кг/м3) (1). Данное опред-е справедливо для однородной ж, имеющей одинаковую интенсив-сть распределения массы по объему. Для неоднород-й ж (1) позволяет найти среднюю плотность по объему. Плотность неоднородной ж в нек-ой точке А опред-ся след-им образом: ρА=limΔV-0
(кг/м3) (1). Данное опред-е справедливо для однородной ж, имеющей одинаковую интенсив-сть распределения массы по объему. Для неоднород-й ж (1) позволяет найти среднюю плотность по объему. Плотность неоднородной ж в нек-ой точке А опред-ся след-им образом: ρА=limΔV-0 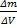 , где Δm- масса малого объема ΔV, к-ый стягивается в т. А. Плотность зависит от давления и температуры. Для технических ж увеличение давления, влечет за собой увеличение плотности, увеличение температуры, влечет за собой уменьшение плотности. Ф(р,ρ,t)=0 – уравнение состояния. С плотностью связаны след- е параметры: 1. Относительная плотность (δ) δ=
, где Δm- масса малого объема ΔV, к-ый стягивается в т. А. Плотность зависит от давления и температуры. Для технических ж увеличение давления, влечет за собой увеличение плотности, увеличение температуры, влечет за собой уменьшение плотности. Ф(р,ρ,t)=0 – уравнение состояния. С плотностью связаны след- е параметры: 1. Относительная плотность (δ) δ= 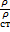 , ρст- плотность стандартного тела, в кач-ве к-го дестилтрованная вода при темпер-ре 4 градуса, ра=760 мм РТ ст. 2. Удельные объем – объем единицы массы ж. (v) v=
, ρст- плотность стандартного тела, в кач-ве к-го дестилтрованная вода при темпер-ре 4 градуса, ра=760 мм РТ ст. 2. Удельные объем – объем единицы массы ж. (v) v=  =
=  , м3/кг 3. удельный вес – это отношение веса ж к объеиу, к-ый она занимает γ=
, м3/кг 3. удельный вес – это отношение веса ж к объеиу, к-ый она занимает γ=  =
= 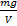 =ρg, g=9,81 м/c2
=ρg, g=9,81 м/c2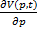 Δp+-
Δp+- 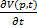 Δt+… Найти абсолютное приращение объема ж: ΔV=V(p+Δp; t+Δt)- V(p,T)=- -
Δt+… Найти абсолютное приращение объема ж: ΔV=V(p+Δp; t+Δt)- V(p,T)=- - 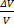 =-
=-  (- -
(- - 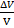 с приращением давления Δр и темпер-ры Δt.
с приращением давления Δр и темпер-ры Δt.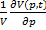 , (1/Па) (2). Он характеризует относительное изменение объема ж при изменении давления на 1 Па при фиксированном знач-ии темпер-ры t. Под действием давления ж сжимается, меняет форму. Величина, обратная коэф-ту сжатия наз-ся изотермическим модулем упругости (к), к= 1/βр, (Па) (3).
, (1/Па) (2). Он характеризует относительное изменение объема ж при изменении давления на 1 Па при фиксированном знач-ии темпер-ры t. Под действием давления ж сжимается, меняет форму. Величина, обратная коэф-ту сжатия наз-ся изотермическим модулем упругости (к), к= 1/βр, (Па) (3).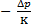 + βtΔt (5).
+ βtΔt (5).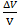 =
= 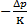 Полученное соотношение представляет собой обобщенный з-н Гука. Роберт Гук англ естествоиспытатель. Растяжение пружины: какого удлинение, такова и сила. Какого сжатие ж, такого и давление. К- модуль упругости. Квода=2060МПа, можно показать, что
Полученное соотношение представляет собой обобщенный з-н Гука. Роберт Гук англ естествоиспытатель. Растяжение пружины: какого удлинение, такова и сила. Какого сжатие ж, такого и давление. К- модуль упругости. Квода=2060МПа, можно показать, что 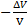 =
= 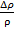 , т.е убыль относ-го объема ж = приращению относит-ой плотности ж.
, т.е убыль относ-го объема ж = приращению относит-ой плотности ж. 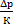 ,
, 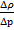 =
=  =а2, (м/c)2. А-скорость распространения волны деформации в ж, к-я наз-ся скоротью звука в ж. а=
=а2, (м/c)2. А-скорость распространения волны деформации в ж, к-я наз-ся скоротью звука в ж. а= 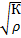 . Упругость ж. м.б оценена изотермич-им коэф-ом βр, изотермическим модулем упругости К, скоростью звука в ж. а. К=1/ βр, а=
. Упругость ж. м.б оценена изотермич-им коэф-ом βр, изотермическим модулем упругости К, скоростью звука в ж. а. К=1/ βр, а= 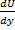 , (Н) (6) – з-н внутр-го трения Ньютона: S- площадь соприкасающихся слоев,
, (Н) (6) – з-н внутр-го трения Ньютона: S- площадь соприкасающихся слоев,  СИ (1м2/c), СГС (1стокс), 1Ст=10-4м2/c, 1cCт=10-6м2/c. Вязкость зависит от рода и хим состава жидкости, температуры и давления. Увеличение температуры приводит к снижению вязкости. Увеличение давления приводит к незначительному увеличению µ. Гипотеза Ньютона была экспериментально подтверждена Шарлем Кулоном и Петровым. Ж в к-х сила внутр-го трения следует з-ну Ньютона наз-ся Ньютоновскими или нормальными жидкостями. К ним относ-ся вода, бензин, керосин, большинство минерал-х масел, используемых в технике. Ж не подчиняющаяся з-ну Ньютона наз-ся неньютоновскими или аномальными: смолы, нек-е масла при темпер-ре близкой к темпер-ре замерзания, каллоиды.
СИ (1м2/c), СГС (1стокс), 1Ст=10-4м2/c, 1cCт=10-6м2/c. Вязкость зависит от рода и хим состава жидкости, температуры и давления. Увеличение температуры приводит к снижению вязкости. Увеличение давления приводит к незначительному увеличению µ. Гипотеза Ньютона была экспериментально подтверждена Шарлем Кулоном и Петровым. Ж в к-х сила внутр-го трения следует з-ну Ньютона наз-ся Ньютоновскими или нормальными жидкостями. К ним относ-ся вода, бензин, керосин, большинство минерал-х масел, используемых в технике. Ж не подчиняющаяся з-ну Ньютона наз-ся неньютоновскими или аномальными: смолы, нек-е масла при темпер-ре близкой к темпер-ре замерзания, каллоиды.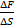 =
= 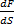 (1)
(1) ≠0,
≠0,  ≠0,
≠0, 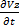 ≠0 – условие нестационарности движ-я. N:1 Быстрое опоражнение сосуда в отверстии в дне. 2. Движ-е ж во всасывающем и нагнетающем трубопроводов поршневого насоса. 2. Установившееся или стационарное движ-е – это движ-е ж с неизменными во времени местными скоростями.
≠0 – условие нестационарности движ-я. N:1 Быстрое опоражнение сосуда в отверстии в дне. 2. Движ-е ж во всасывающем и нагнетающем трубопроводов поршневого насоса. 2. Установившееся или стационарное движ-е – это движ-е ж с неизменными во времени местными скоростями. 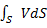 =Q, Vср одинакова по всему сечению. Коэфициент Корриолиса, учитывающий неравномерность распред-я местных скоростей по сеч-ю при переходе к средней скорости =2 (т.е α=2). 2. Турбулентное движ-е ж – это течение, сопровождающееся интенсивным перемешиванием ж пульсации скоростей и давлений. Движ-е частиц неупорядоченное, имеют место поперечное движ-е частиц и вращательные движ-я отдельных объемов ж. Турбулентный в переводе с лат – возмущенный, вихревой, бурный. При турбулентном движ-ии местные скорости измен-ся не только по направлению, но и во времени, они пульсируют. Рис.В связи с этим вводят в рассмотрение усредненную по времени местную скорость. Vуср=
=Q, Vср одинакова по всему сечению. Коэфициент Корриолиса, учитывающий неравномерность распред-я местных скоростей по сеч-ю при переходе к средней скорости =2 (т.е α=2). 2. Турбулентное движ-е ж – это течение, сопровождающееся интенсивным перемешиванием ж пульсации скоростей и давлений. Движ-е частиц неупорядоченное, имеют место поперечное движ-е частиц и вращательные движ-я отдельных объемов ж. Турбулентный в переводе с лат – возмущенный, вихревой, бурный. При турбулентном движ-ии местные скорости измен-ся не только по направлению, но и во времени, они пульсируют. Рис.В связи с этим вводят в рассмотрение усредненную по времени местную скорость. Vуср= 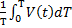 , Т-интервал усреднения, усредненная скорость не зависит от времени. Эпюра распределения по сечению потока усредненных по времени местных скоростей опред-ся структурой турбулентного потока. В соответствии с полуэмпирической теорией турбулентности: он состоит (турбул-й поток) из турбул-го ядра и тонкого ламинарного слоя у стенки. Рис. Для этого режима Vср=
, Т-интервал усреднения, усредненная скорость не зависит от времени. Эпюра распределения по сечению потока усредненных по времени местных скоростей опред-ся структурой турбулентного потока. В соответствии с полуэмпирической теорией турбулентности: он состоит (турбул-й поток) из турбул-го ядра и тонкого ламинарного слоя у стенки. Рис. Для этого режима Vср= 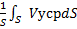 =Q/S, Vср явл-ся результатом двойного осреднения по времени и сечению. Коэффициент Корриолиса α=1,1. Турбул-е движение ж явл-ся нестационарным и неравномерным. Однако, двойное усреднение местных скоростей позволяет условно считать поток установившимся и равномерным относительно средних скоростей – это позволяет применять урав-е Бернулли для таких потоков, где скоростной напор выраж-ся через среднюю скорость.
=Q/S, Vср явл-ся результатом двойного осреднения по времени и сечению. Коэффициент Корриолиса α=1,1. Турбул-е движение ж явл-ся нестационарным и неравномерным. Однако, двойное усреднение местных скоростей позволяет условно считать поток установившимся и равномерным относительно средних скоростей – это позволяет применять урав-е Бернулли для таких потоков, где скоростной напор выраж-ся через среднюю скорость.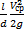 + ∑ ζ
+ ∑ ζ  = (
= ( ∑li+∑ζi)
∑li+∑ζi)  =(
=( Q2=R(Q)Q2
Q2=R(Q)Q2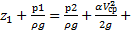 ζ
ζ 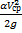 - потери напора на выходе из отверстия: вся кинет-я энергия струи расход-ся на вихреобразования, поэтому потери = скоростному напору.
- потери напора на выходе из отверстия: вся кинет-я энергия струи расход-ся на вихреобразования, поэтому потери = скоростному напору.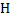 =
= 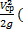 ζ+α) - - Vср=
ζ+α) - - Vср= 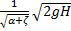 =ф
=ф 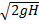 , Q= VсSс=µS0
, Q= VсSс=µS0 


