
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения об относительном покое Ж.Содержание книги
Поиск на нашем сайте
В гидростатике рассм-ся состояние ж, при к-ом все ее очки наход-ся в состоянии покоя по отношению к выбранному телу остчета. Различают абсолютный и относительный покой. Покой ж. относ-но Земли назыв-ся абсолюным, тело отсчета – Земля. Относительный покой – это покой ж, относит-но равноускоренно – движущегося сосуда, в к-ом она наход-ся. Здесь тело отсчета – сосуд. Абсолютный покой наблюд-ся в абсолютной сист координат, относит-й покой наблюд-ся в относит-ой системе координат, связанной с сосудом. Для описания относит-го покоя м.б использованы соотношения, полученные для абс-го покоя. Если в них под координ-ми x,y,z понимать относ-е координаты, а к действующим на жид-ть силам добавить еще одну массовую силу – переносную силу инерции. По виду переносного движ-я можно выделить 2 характер-х случая: 1. Относит-й покой ж в сосуде движущейся прямолинейно и равноускоренно и 2. Относит-й покой ж в сосуде вращающимся относит-но вертик-ой оси с постоянной угловой скоростью. При этом выясним: Каким будут поверх=ти равного давления и Как найти ГСД в произвольной точке ж в сосуде. Для описания относ-го покоя ж воспольз-ся соотношениями: xdx+ydy+zdz=0 (1) –ур-е поверхностей равного давления, dp=ρ(xdx+ydy+zdz) (2). Для решения поставленных задач в соотношении 1 и 2 необходимо подставить соответ-е проекции результирующей массовых сил x,y,z, определенные с учетом переносного ускорения. 19-20.Относительный покой ж в сосуде, движущимся прямолинейно, горизонтально и равноускоренно. Рис. С этим сосудом свяжем относит-ю систему координат. Будем наблюдать покой. Чтобы воспользоваться соотношениями (1) и (2) необходимо к действующей на ж. силе тяжести добавить переносную силу инерции, направленную в сторону противоположную ускорению сосуда А. Тогда на произвольно выбранную точку будут действовать ускорение свободного падения и переносное ускорение, равное ускорению сосуда, взятому с «-», т.е –а. Результирующая этих ускорений j ={x,y,z}, x=-a, y=0,z=-g (3). А) Уравнение поверх-ти равного давления (УПРД) (3)- - (1): -adx-gdz=0, z=- a/g=tgα. Построим след свободные поверх-ти: 1. а увелич-ся, α увелич-ся. 2. а - -∞, α -- - В) Давление в произвольной точке. (3) - - (2) dp=-ρadx-ρgdz (6*) p=-ρax-ρgz+C, где С постоянная интегрирования. «С» можно найти через известные вел-ны на свободной поверх-ти х=0, z=z0, p0 (6), (6) - - (6*):p0=-ρa0-ρgz0+C, C=p0+ρgz0 - - (6*) p=-ρax-ρgz+p0+ρgz0=p0+ρg(z0-z)-ρax, -ρax- добавка к гидростат-му давлению за счет прямолинейного гориз-го, равноускоренного сосуда.
Относительный покой в сосуде, вращающимся вокруг продольной оси с постоянной угловой скоростью. Изобразим сосуд, к-й вращ-ся вокруг вертик оси.. Рис. Система координат жестко закреплена с сосудом и вращ-ся вместе с ним. Задачу об относит-м покое сведем к задаче абс-го покоя, добавляя к действующей на жид-ть силы тяжести переносную силу инерции. Переносное движение – это вращ-е сосуда. Переностной силой инерции явл-ся центробежная сила. Тогда в произвольной точке А будет приложено ускорение своб-го падения g и центробеж-е ускорение w2r, j{x,y,z}. x=w2rcos(r,x)=w2x, y=w2rsin(r,x)=w2, z=-g, x=w2x, y=w2y, z=-g (7) А) УПРД: (7) - -(1) w2xdx+w2ydy-gdz=0, w2x2/2+w2y2/2-gz=C, (w2/2)*(x2+y2)-gz=C (8), С постоянная интегрирования. Ур-е (8) –это ур-е оверхностей равного давления. Оно дает семейство конгру-ых (??) (совмещающихся при наличии парабалоидов вращ-я). Пусть парабалоид вращения с вершиной x=0, y=0, z=z0 (8*) явл-ся параболоидом свободной поверх-ти. Величина z0 зависит от объема ж в сосуде и угловой скорости w. Подставим (8*) в (8): -gz0=C - -C=-gz0, C- - (8), (w2/2)*(x2+y2)-gz=-gz0, =z0+(w2/2)*(x2+y2) – уравнение парабалоида свобод-й пов-ти. В)Давление в произвольной точке (7) в (2): dp=ρ(w2xdx+w2ydy-gdz), p=ρ(w2xdx+w2ydy-gdz)+c (9*) C-? x=0,y=0,z=z0, p0 (9), (9) в (9*) p0=-ρgz0+C, C=p0-ρgz0, p=ρ(w2xdx+w2ydy-gdz)+ p0-ρgz0, p=p0+ρg(z0-z)+ (ρw2/2)*(x2+y2), (ρw2/2)*(x2+y2)-добавка к гидростат-му давлению за счет вращ-я сосуда.
Виды движения ж. Кинематика ж – раздел гидравлики, кй изучает движ-е ж без учета причин, к-е его вызывают (а вызывают движ-е массовые силы). Рассм-м движ-е ж в простр-ве, ограниченном направляющими поверхностями. С этим простр-ом свяжем прямоуг-ю систему координат 0xyz. Рис. Скорость ж в заданной точке пространства наз-ся местной скоростью. Она явл-ся непрерывной функцией координат точки и времени. V=V(x,y,z,t)={Vx(x,y,z,t),Vy(x,y,z,t), Vz(x,y,z,t)}= {Vx, Vy, Vz}. Задача кинематики ж заключ-ся в определении скоростей движ-я в различных точках пространств, т.е в нахождении поля местных скоростей. Классификация видов движения: По характеру изменения поля скоростей во времени движ-я ж подраздел-ся на 1. неустановив-е или нестационарное движ-е ж с изменяющимся во времени местными скоростями По характеру изменения поля скоростей в пространстве установившееся движ-е ж м.б: неравномрным, равномерным, плавноизменяющимся. 1. При неравномерном движ-ии местные скорости мен-ся в простр-ве по вел-не и направ-ю. N: установив-сядвиж-е ж в местах деформации потока. 2. При равномерном движ-ии местная скорость неизменна во всех точках пространства. N: установ-ся движ-е ж в прямолин-м цилиндрическом трубопроводе. 3. Плавно – изменяющееся движ-е хар-ся плавным изменением поля скорости в пространстве. К нему применимы законы равномерного движ-я. N: плавный поворот.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.109.60 (0.005 с.) |

 x+C, С постоянная интегрирования. Ур-е (4) – это ур-е поверхностей равного давления жидкости в сосуде, движущимся гориз-но, прямолинейно и равноускоренно. Оно дает семейство плоскостей, наклонных к осям z и х и параллельных к оси y. Свободная поверх-ть явл-ся одной из поверх-ей равного давления. Найдем урав-е свободной пов-ти. Задача состоит в том, чтобы из бесконечной совокупности плоскостей равного давления выделить свободную поверхность путем подбора постоянной интегрирования С. Пусть свободная пов-ть проходит через точку х=0, z=z0 (5) (4)--:z0=-(a/g)*0+C - - C=z0- - (4): z=-(a/g)*x+z0 – ур-е свободной поверх-ти
x+C, С постоянная интегрирования. Ур-е (4) – это ур-е поверхностей равного давления жидкости в сосуде, движущимся гориз-но, прямолинейно и равноускоренно. Оно дает семейство плоскостей, наклонных к осям z и х и параллельных к оси y. Свободная поверх-ть явл-ся одной из поверх-ей равного давления. Найдем урав-е свободной пов-ти. Задача состоит в том, чтобы из бесконечной совокупности плоскостей равного давления выделить свободную поверхность путем подбора постоянной интегрирования С. Пусть свободная пов-ть проходит через точку х=0, z=z0 (5) (4)--:z0=-(a/g)*0+C - - C=z0- - (4): z=-(a/g)*x+z0 – ур-е свободной поверх-ти . 3. А=0, z=z0 – ур-е гориз-й плоск-ти, абсол-й покой. Координата z0 определ-ся из равенства объемов ж в сосуде при относ-ом и абсолютном покоях.
. 3. А=0, z=z0 – ур-е гориз-й плоск-ти, абсол-й покой. Координата z0 определ-ся из равенства объемов ж в сосуде при относ-ом и абсолютном покоях. ≠0,
≠0,  ≠0,
≠0, 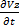 ≠0 – условие нестационарности движ-я. N:1 Быстрое опоражнение сосуда в отверстии в дне. 2. Движ-е ж во всасывающем и нагнетающем трубопроводов поршневого насоса. 2. Установившееся или стационарное движ-е – это движ-е ж с неизменными во времени местными скоростями.
≠0 – условие нестационарности движ-я. N:1 Быстрое опоражнение сосуда в отверстии в дне. 2. Движ-е ж во всасывающем и нагнетающем трубопроводов поршневого насоса. 2. Установившееся или стационарное движ-е – это движ-е ж с неизменными во времени местными скоростями. 


