
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение физических величин и вычисление погрешностейСодержание книги
Поиск на нашем сайте
Введение
Профессиональная подготовка товароведов и таможенников определяется глубоким знанием естественных наук и умением применять их на практике. Став специалистом, товаровед должен систематически повышать уровень знаний, расширять свой кругозор, уделять внимание освоению качественного новых методов исследования товаров, сырья и материалов. Так как большинство свойств, которыми обладает товар, - физические, то наиболее широко используются физические методы исследования. Их преимущество состоит в том, что можно получить необходимые сведения, не разрушая образец. Следовательно, в условиях непрерывного расширения и усложнения ассортимента товаров, повышения требований к уровню их качества возрастает роль физической науки как основы методов товароведной оценки качества товаров. В таблице 1 представлены основные физические методы используемые в экспертизе качества и потребительских свойств товаров, сырья и материалов. Таблица 1
Только эти методы количественного анализа товаров дают представление о том, что физические методы исследования занимают достойное место.
Совокупность свойств товаров сырья и материалов, обуславливающих их пригодность удовлетворять определенные потребности, определяет качество продукции. В понятие качество входит и наличие определенных физических свойств: основные физические свойства, структурно-механические, теплофизические, оптические и др. Эти свойства базируются на тех понятиях, определениях и законах, которые изучаются в курсе общей физики. Так, например, - при изучении термических свойств промышленных товаров (меха, утеплителя одежды, обуви и т.д.) используются знания о явлении теплопроводности; - при изучении физико-химических свойств необходимы знания о влажности воздуха (абсолютная и относительная влажность воздуха); - при использовании капиллярного метода дефектоскопии применяются знания о свойствах жидкостей (смачивание, капиллярные явления); - при изучении механических свойств материалов (ткани, кожа, фарфор и т.д.) используются знания о видах деформации, знания об основных механических свойствах твердых тел (упругость, пластичность, хрупкость, твердость); - при изучении термических свойств материалов (теплоемкость, теплопроводность, термическое расширение и др.) используются знания о тепловых свойствах твердых тел; - при изучении влияния электрического поля на качество многих промышленных товаров используются знания поведения диэлектриков и проводников в электрическом поле; - при изучении принципа работы электронных приборов и электротоваров используется зонная теория проводимости, знания о действии магнитного поля на проводник с током; - при изучении свойств кино- и фототоваров используются знания о волновых свойствах света (явление интерференции, дифракции и поляризации света); - при исследованиях микроструктуры веществ используются знания, изучаемые в таких разделах физики как атомная физика, ядерная физика и физика твердого тела.
Таким образом, можно без преувеличения сказать, что физика не только нужна товароведу, а научно обоснованного товароведения, соответствующего научно техническому прогрессу, не может быть без опоры на физику. Физика – фундаментальная наука не только в принципе, она фундаментальная и в более узком смысле слова – для товароведения. В этой связи, задачей лабораторного практикума, предусмотренного в учебных программах курса “физика и методы исследования сырья и материалов” для соответствующих специальностей, является закрепление теоретического материала изучаемых разделов физики и выработка навыков измерений физических величин, используемых в исследованиях потребительских качеств товаров, продуктов, сырья и материалов.
ОФОРМЛЕНИЕ ОТЧЕТА ПО РАБОТЕ Для оформления отчетов по физическому практикуму необходимо иметь специальный журнал экспериментальной работы или специальные бланки для каждой работы отдельно. Заполнение бланка или журнала отчета проводят по следующей схеме: 1. Записывают название и номер работы. 2. Дают краткое описание метода и приборов с показом схем приборов и установок. 3. В таблицу записи измерений вписывают результаты всех первичных измерений (берут из опытов). 4. По расчетной формуле проводят вычисление искомой величины. 5. Вычисляют погрешности измерения. 6. Строят график.
Второй пункт отчета рекомендуется заполнять дома. Как показывает вычислительная практика, успех всякой экспериментальной работы зависит не только от правильности выбора метода измерения, точности применяемых приборов, тщательности выполнения измерений, но и от правильной систематической записи результатов измерений. Привычка производить вычисления на случайных клочках бумаги совершенно не допустима даже в черновых отчетах. Необходимо систематически воспитывать в себе навыки точной, аккуратной и своевременной фиксации всех измерений. Все вычисления физических величин следует проводить в Международной системе единиц (СИ).
ЧАСТЬ 1 ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА.
ЛАБОРАТОРНАЯ РАБОТА № 1 ИССЛЕДОВАНИЕ УПРУГОГО УДАРА ШАРОВ Цель работы: закрепление теоретического материала по теме "Законы сохранения в механике". Задачи работы: вычислить работу деформации и коэффициент восстановления при соударении стальных шаров. Приборы и принадлежности: Специальная установка для исследования упругого удара шаров. Краткая теория Понятие " удар " включает в себя совокупность явлений, возникающих при столкновении движущихся твердых тел, а также при некоторых видах взаимодействия твердого тела с жидкостью или газом (например, удар струи о тело, действие взрывной волны на твердое тело и др.). Промежуток времени, в течение которого длится удар, обычно очень мал (~ 10-4 - 10-5с), а развивающиеся на площадках контакта соударяющихся тел ударные силы очень велики. За время удара они изменяются в широких пределах и достигают значений, при которых средние величины давления (напряжений) на площадках контакта имеют порядок 104-105 атм. Действие ударных сил приводит к значительному Следствиями удара могут быть остаточные деформации, звуковые колебания, нагревание тел, изменение механических свойств материалов (в частности, их упрочнение), полиморфные и химические превращения и др., а при скоростях соударения, превышающих критические, - разрушение тел в месте удара. Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий. Абсолютно упругим называется удар, после которого тела полностью восстанавливают свою первоначальную форму и совершают самостоятельное движение. Абсолютно неупругим называется удар, после которого деформация тел сохраняется и тела совершают совместное движение. При абсолютно упругом ударе выполняются закон сохранения импульса и закон сохранения механической энергии. При абсолютно неупругом ударе закон сохранения механической энергии не выполняется, т.к. часть механической энергии идет на образование остаточных деформаций, нагревание тел и др. Рассмотрим упругое столкновение двух тел. Пусть совершается "центральный удар", при котором центры масс соударяющихся тел движутся по одной прямой, при этом вращательного движения не возникает. В процессе удара возникают кратковременные ударные силы, величина которых много больше всех остальных сил (силы тяжести, сил сопротивления воздуха и т. д.). Поэтому систему соударяющихся тел можно считать изолированной и записать для нее законы сохранения: Закон сохранения механической энергии:
и закон сохранения импульса:
где V
Решая совместно уравнения (1) и (2), получим формулы для расчета скоростей тел после упругого удара:
В них принимается направление скорости Формулы (1) - (4) применимы в случае столкновения абсолютно упругих тел. При столкновении реальных тел в формуле (1) следует учесть ту часть механической энергии, которая расходуется на совершение невосстанавливающейся деформации и преобразуется в энергию теплового движения (диссипация энергии) - работу деформации А:
По величине "А" оценивают степень " неупругости " удара. По предложению Ньютона степень " неупругости " удара оценивают и по отношению нормальных составляющих скоростей тел после и до удара.
где Vn,
Это отношение называют коэффициентом восстановления
Метод измерения В данной работе изучается прямой удар двух шаров из стали, подвешенных на нитях так, что в момент удара они проходят через положение равновесия. При центральном ударе двух шаров одинаковых масс
найдем из следующих соображений. Потенциальная энергия шара в момент удара полностью превращается в кинетическую:
Равенство (8) соблюдается и после удара:
Тогда из уравнения (8) и (9) имеем: Следовательно:
Но:
где:
Подставляя (11) в (10), окончательно получим:
Работа деформации определяется из уравнения (5), в котором кинетические энергии заменяются потенциальными, а высоты через углы по формулам (11). После подстановки окончательно получим:
Литература 1. Курс общей физики. Том 1. Савельев И.С. 2. Курс физики. Том 1. Яворский Б.М., Детлаф А.А. 3. Курс общей физики. Шубин И.В.
h
Рис.1 ЛАБОРАТОРНАЯ РАБОТА №2 И СИЛЫ ТРЕНИЯ В ОПОРЕ Цель работы: Закрепление теоретического материала по теме "Динамика вращательного движения твердого тела". Задачи: Вычислить момент инерции махового колеса и силу трения в опоре. Приборы и принадлежности: Прибор, состоящий из махового колеса, укрепленного на стене, масштабная линейка, штангенциркуль, секундомер, шнур с грузом. Краткая теория Твердое тело можно рассматривать как систему материальных точек, расстояние между которыми неизменно. Вращательным движением твердого тела называют такое движение, при котором все точки тела описывают окружности вокруг некоторой оси вращения. Если тело может вращаться вокруг неподвижной оси, то изменение его движения зависит от действующего на тело момента силы. Моментом силы
Вращательное движение твердого тела характеризуется угловой скоростью Угловой скоростью вращения называется вектор
Угловым ускорением называется вектор
Моментом инерции материальной точки относительно оси вращения называют скалярную физическую величину, численно равную произведению массы этой точки на квадрат расстояния её до оси вращения:
Момент инерции твердого тела равен сумме моментов инерций материальных точек:
Зависимость углового ускорения действующей на тело силы и момента инерции
Рис. 1
угловое ускорение Если сопоставить законы поступательного и вращательного движений, легко сделать вывод, что момент инерции во вращательном движении выполняет ту же роль, что и масса в поступательном движении, так момент инерции характеризует инертность тела во вращательном движении. Вращающееся тело обладает кинетической энергией:
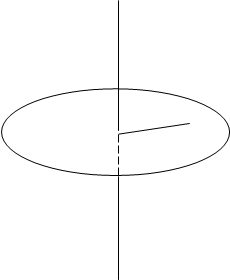
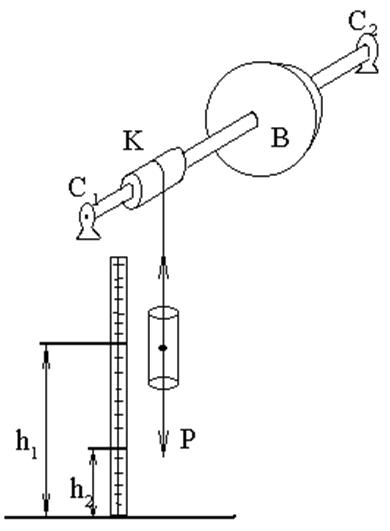
Момент инерции махового колеса и силу трения вала в опоре можно определить при помощи прибора, изображенного на рисунке 2.
Рис. 2
Прибор состоит из махового колеса B, укрепленного на валу. Вал установлен на шарикоподшипниках движение грузом Р. Груз Р на какой - то высоте Если предоставить возможность грузу падать, то потенциальная энергия
Движение груза - равноускоренное без начальной скорости, поэтому ускорение а и скорость
где t - время опускания груза с высоты h1. Найдем угловую скорость махового колеса по формуле:
где Сила трения Уменьшение потенциальной энергии при подъеме груза равно работе по преодолению силы трения в опорах
отсюда
Подставляя в формулу (8) значения V,
Порядок выполнения работы. 1. Наматывая на шкив шнур, поднять груз на высоту 2. Отпустить груз и секундомером измерить время падения груза с высоты 3. Определить высоту 4. Измерить штангенциркулем радиус шкива
Контрольные вопросы
1. Что называют моментом инерции материальной точки, твердого тела относительно оси вращения? В каких единицах измеряется? 2. Что называется моментом силы относительно оси вращения? Как записывается основной закон динамики для вращательного движения? 3. Чему равна кинетическая энергия вращающегося тела? 4. Как определить линейное ускорение груза и угловое ускорение колеса? 5. Какой закон положен в основу вывода расчетных формул?
Литература 1. Курс общей физики. Том 1. Савельев И.С. 2. Курс физики. Том 1. Яворской Б.М., Детлаф А.А. 3. Курс общей физики. Шубин И.В.
ЛАБОРАТОРНАЯ РАБОТА №3 Краткая теория Сила характеризует действие одного тела на другое. В результате этого воздействия тело может прийти в движение или деформироваться. Деформацией твердого тела называется изменение взаимного расположения частиц тела, которое приводит к изменению формы и размеров тела и вызывает изменение сил взаимодействия между частицами, т. е. возникновение напряжений. Деформируемыми являются все вещества. Деформация может быть следствием теплового расширения, воздействия электрических и магнитных полей, а также внешних механических сил. В твердых телах деформация называется упругой, если она исчезает после снятия нагрузки, и пластической, если она после снятия нагрузки не исчезает. Внутри деформированного тела возникает противодействующая сила, равная по величине деформирующей силе и называемая силой упругости. Силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) тела и имеют электрическую природу. Физическая величина, численно равная упругой силе
Английский физик Р. Гук экспериментально установил, что напряжение
где
Относительная деформация равна отношению абсолютной деформации
Рассмотрим упругую деформацию одностороннего растяжения проволоки (рис. 1)
приложим силу
и в ней возникнет сила упругости По закону Гука напряжение проволоке, прямо пропорционально относительной
Рис. 1 Е =
Если положить, что Заменив в формуле (2) напряжение и относительное удлинение по формулам
Площадь поперечного сечения проволоки Подставив выражение (4) в (3) и учитывая, что
Порядок выполнения работы 1. Отметим на исследуемой проволоке какую-нибудь точку, для чего укрепим на ней кусочек тонкой проволоки. 2. Наведем на эту точку отсчетный микроскоп и заметим деление 3. Определяем удлинение проволоки, вызванное нагрузкой
Здесь 4. Вычисляем модуль Юнга по формуле (5), значение 5. Опыты повторить с другими значениями масс 6. Результаты опытов занести в таблицу:
Контрольные вопросы 1.Что называется деформацией, виды деформаций? 2.Какими величинами характеризуют деформацию растяжения (сжатия)? 3.Как читается закон Гука и для каких деформаций он справедлив? 4.Какой физический смысл модуля Юнга?
Литература. 1. Детлаф А.А., Яворский Б.М., Милковская Л.Б. "Курс физики" ч.1. 2. Шубин А.С. "Курс общей Физики". 3. Грабовский Р.И. "Курс физики".
ЛАБОРАТОРНАЯ РАБОТА № 4 Краткая теория
Раздел физики, в котором рассматривают законы равновесия и движения жидких и газообразных тел, а также их взаимодействия с твердыми телами, называют гидроаэромеханикой. Характерное свойство жидких и газообразных тел – их текучесть, т.е. малая сопротивляемость деформации сдвига: если скорость сдвига стремится к нулю, то силы сопротивления жидкости или газа этой деформации также стремятся к нулю. Иными словами, жидкие и газообразные тела не обладают упругостью формы – они легко принимают форму того сосуда, в котором находятся. Вследствие этого внешнее давление, производимое на жидкость или газ, передается ими во все стороны равномерно (закон Паскаля). Движение жидкостей или газов называют течением, а совокупность частиц движущейся жидкости или газа называют потоком. В гидромеханике отвлекаются от молекулярного строения жидкостей и газов, рассматривая их как сплошную среду. Течение жидкости называют установившимся или стационарным, если скорость жидкости в каждой точке пространства, занятого жидкостью, не изменяется с течением времени, т.е. V не зависит от t. В случае неустановившегося течения V зависит также от времени t. Течение называют ламинарным или слоистым в том случае, если поток представляет собой совокупность слоев, перемещающихся друг относительно друга без перемешивания. Течение называют турбулентным, если имеет место перемешивание различных слоев жидкости или газа вследствие образующихся завихрений. В целях наглядности движение жидкости можно изображать с помощью линий тока, которые проводят так, что касательные к ним совпадают по направлению с векторами скоростей жидкости в соответствующих точках пространства. В случае стационарного течения линии тока не изменяются с течением времени и совпадают с траекториями отдельных частиц жидкости. Поверхность, которая образована линиями тока, проведенными через все точки малого замкнутого контура, называют трубкой тока. Часть жидкости, ограниченную трубкой тока, называют струей. В реальных жидкостях течение усложняется тем, что между отдельными слоями потока происходит внутреннее трение. Однако в ряде случаев влияние внутреннего трения невелико и им можно пренебречь. Жидкость, в которой отсутствует внутреннее трение, называют идеальной жидкостью. Поэтому изучая движение идеальной жидкости, можно установить ряд закономерностей, которые с известным приближением применимы к течению реальных жидкостей. При переходе потока жидкости из трубки с большим диаметром Д или для двух сечений: S Если S= Изменение скорости течения влечет изменение давления, которое можно определить из уравнения Бернулли:
Для горизонтальной трубки уравнение Бернулли запишется:
P Где P |

 изменению за время удара скоростей точек тела.
изменению за время удара скоростей точек тела.
 (1)
(1) , (2)
, (2)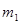 и
и 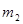 массы тел,
массы тел, и V
и V  - скорости тел до удара,
- скорости тел до удара, и
и  - скорости тел после удара.
- скорости тел после удара. (3)
(3)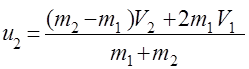 (4)
(4) за положительное. Скорости
за положительное. Скорости  , V
, V  подставляем в формулы с минусом, если их направление противоположно направлению V1.
подставляем в формулы с минусом, если их направление противоположно направлению V1.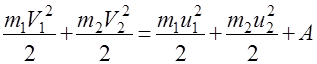 (5)
(5) , (6)
, (6)  - нормальные составляющие скорости до и после удара.
- нормальные составляющие скорости до и после удара. , который зависит от физических свойств материалов тел: (например:
, который зависит от физических свойств материалов тел: (например:  = 0,94,
= 0,94,  и при условии равенства скоростей до удара V1 = V2 = V соблюдается равенство скоростей и после удара
и при условии равенства скоростей до удара V1 = V2 = V соблюдается равенство скоростей и после удара  . Тогда коэффициент восстановления:
. Тогда коэффициент восстановления: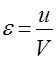 (7)
(7) (8)
(8) (9)
(9) ,
, 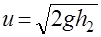
 (10)
(10)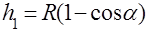 ,
,  , (11)
, (11)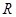 - длина нити,
- длина нити,  - угол отклонения после удара,
- угол отклонения после удара, - угол отклонения до удара.
- угол отклонения до удара. (12)
(12)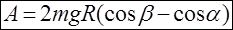 (13)
(13)
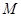 относительно неподвижной оси называется векторная физическая величина, численно равная произведению силы
относительно неподвижной оси называется векторная физическая величина, численно равная произведению силы 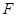 на её плечо
на её плечо 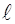 , т.е. кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила:
, т.е. кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила: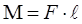 (1)
(1) и угловым ускорением
и угловым ускорением  , численно равный первой производной от угла поворота
, численно равный первой производной от угла поворота 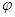 радиуса-вектора по времени и направленный вдоль оси вращения так, что из его конца вращение видно происходящим против часовой стрелки:
радиуса-вектора по времени и направленный вдоль оси вращения так, что из его конца вращение видно происходящим против часовой стрелки: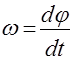 (2)
(2)  , равный первой производной от угловой скорости по времени:
, равный первой производной от угловой скорости по времени: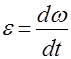 (3)
(3)
 (4)
(4)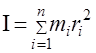 (5)
(5)
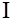 тела выражается вторым законом Ньютона
тела выражается вторым законом Ньютона для вращательного движения (основным
для вращательного движения (основным 
 законом динамики вращательного движения):
законом динамики вращательного движения):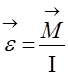 (6) и читается:
(6) и читается: (7)
(7)
 и
и  . Маховое колесо приводится во вращательное
. Маховое колесо приводится во вращательное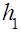 обладает потенциальной энергией
обладает потенциальной энергией 
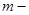 масса груза.
масса груза. груза перейдет в кинетическую энергию
груза перейдет в кинетическую энергию 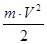 поступательного движения груза, кинетическую энергию вращательного движения
поступательного движения груза, кинетическую энергию вращательного движения 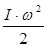 прибора и в работу
прибора и в работу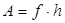 по преодолению силы трения
по преодолению силы трения  в опоре. По закону сохранения энергии
в опоре. По закону сохранения энергии (8)
(8) соответственно равны:
соответственно равны: ;
;  , (9)
, (9)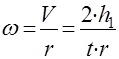 , (10)
, (10) - радиус вала, на который намотана нить.
- радиус вала, на который намотана нить.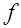 вычисляется следующим образом. После опускания груза колесо, вращаясь по инерции, поднимает груз на высоту
вычисляется следующим образом. После опускания груза колесо, вращаясь по инерции, поднимает груз на высоту 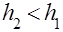 , и потенциальная энергия груза на высоте
, и потенциальная энергия груза на высоте 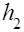 будет равна
будет равна  .
.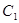 и
и  , т. е.
, т. е. ,
,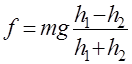 (11)
(11) (12)
(12) и вычислить момент инерции махового колеса и силу трения в опоре по формулам (12) и (11). Полученные результаты занести в таблицу. Повторить опыты при других значениях
и вычислить момент инерции махового колеса и силу трения в опоре по формулам (12) и (11). Полученные результаты занести в таблицу. Повторить опыты при других значениях  груза.
груза.


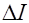
 , приходящейся на единицу площади
, приходящейся на единицу площади  сечение тела, называется напряжением:
сечение тела, называется напряжением:
 при упругих деформациях тела прямо пропорционально его относительной деформации
при упругих деформациях тела прямо пропорционально его относительной деформации  , (1)
, (1)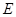 - модуль Юнга (модуль упругости), величина которого определяется свойствами материала, из которого изготовлено тело. Например,
- модуль Юнга (модуль упругости), величина которого определяется свойствами материала, из которого изготовлено тело. Например,  ;
; ;
;  ;
;  .
.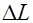 к начальной длине
к начальной длине  :
: (2)
(2)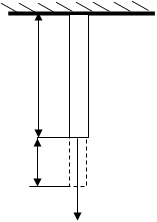 К нижнему концу закрепленной проволоки длиной
К нижнему концу закрепленной проволоки длиной 
 , под действием которой
, под действием которой
 .
. , возникшее в
, возникшее в деформации:
деформации: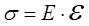 (1),
(1), отсюда модуль Юнга равен:
отсюда модуль Юнга равен:
 , т.е.
, т.е.  , то
, то  , т.е. модуль Юнга численно равен напряжению, возникающему в упруго деформированном теле, при относительной деформации, равной единице.
, т.е. модуль Юнга численно равен напряжению, возникающему в упруго деформированном теле, при относительной деформации, равной единице. и
и  (3)
(3)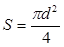 (4), где
(4), где  диаметр проволоки.
диаметр проволоки. , получим расчетную формулу для модуля Юнга:
, получим расчетную формулу для модуля Юнга: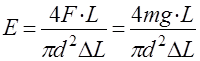 (5)
(5) на шкале микроскопа, которое совпадает с указанной точкой. После этого кладем на чашку груз массой
на шкале микроскопа, которое совпадает с указанной точкой. После этого кладем на чашку груз массой 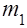 .
. ,
,
 пересчетный коэффициент измерительного микроскопа, переводящий удлинение в делениях шкалы, видимой в окуляре, в миллиметры. Каждому значению длины тубуса микроскопа соответствует свое значение
пересчетный коэффициент измерительного микроскопа, переводящий удлинение в делениях шкалы, видимой в окуляре, в миллиметры. Каждому значению длины тубуса микроскопа соответствует свое значение  , которое указано в таблице на установке.
, которое указано в таблице на установке. и
и  ,
,  .
.






 в трубку с меньшим диаметром Д
в трубку с меньшим диаметром Д  происходит увеличение скорости течения от значения V
происходит увеличение скорости течения от значения V  . Соотношение между скоростями течения V
. Соотношение между скоростями течения V  задается уравнением неразрывности струи: SV = Const
задается уравнением неразрывности струи: SV = Const V
V  ,то уравнение (1) перепишется: V
,то уравнение (1) перепишется: V  Д
Д  = V
= V  Д
Д  (2)
(2)
 , отсюда
, отсюда - P
- P  , (3)
, (3) , V
, V 


