
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория метода и описание установки.Содержание книги
Поиск на нашем сайте
Удельной теплоемкостью С газа называется скалярная физическая величина, численно равная количеству теплоты Q, которое необходимо сообщить единице массы газа, чтобы увеличить его температуру на 1 К:
Величина теплоемкости газов зависит от условий нагревания. Выясним эту зависимость, воспользовавшись первым законом термодинамики, который гласит: количество теплоты Q, сообщенное системе, затрачивается на увеличение ее внутренней энергии
При изохорическом (V=const) нагревании газа
Из формулы (1) следует, что
При изобарном (Р=const) нагревании газа тепло, сообщаемое газу идет и на увеличение внутренней энергии и на совершение газом работы против внешних сил:
поэтому Сравнивая уравнения (3) и (4), получаем Отношение удельных теплоемкостей при постоянном давлении и при постоянном объеме
В данной работе прелагается один из самых простых методов определения метод Клемана и Дезорма. Адиабатическим процессом называется процесс, протекающий без теплообмена с окружающей средой, т.е. считается, что процесс передачи тепла системе от окружающей среды отсутствует. Экспериментальная установка состоит из стеклянного баллона А (рис. 1), соединенного с манометром В и с насосом.
Рис. 1
Если про помощи насоса накачать в баллон некоторое количество воздуха, то давление и температура воздуха внутри баллона повысятся. Вследствие теплообмена воздуха с окружающей средой через некоторое время температура воздуха, находящегося в баллоне, сравнятся с температурой внешней среды Давление, установившееся в баллоне
где Р - атмосферное давление; Н - разность уровней жидкости в манометре; В - коэффициент перехода от разности уровней к давлению. Таким образом, состояние воздуха внутри баллона, которое назовем 1 состоянием, характеризуется параметрами
Если на короткое время открыть кран С, то воздух в баллоне будет расширяться. Этот процесс расширения можно считать адиабатическим. Давление в баллоне установится равным атмосферному Р, температура газа понизится до Следовательно, в конце адиабатического процесса, что назовем 2 состоянием, параметры состояния газа будут Р; Применяя к 1 и 2 состояниям уравнение (5), получим:
Охладившийся при адиабатическом расширении воздух в баллоне через некоторое время вследствие теплообмена нагреется до температуры внешней среды
где h- новая разность уровней в манометре. Объем воздуха не изменится и будет равен Это состояние воздуха, которое назовем 3 состоянием, характеризуется параметрами
Так как в состояниях 1 и 3 воздух имеет одну и ту же температуру (P+вH)
Возведем обе части уравнения в степень
Решая совместно уравнения (6) и (7), получим:
Логарифмируя это выражение и решая относительно
Так как давления Р, Р+вН и Р+вh мало отличаются друг от друга, то разности логарифмов можно принять пропорциональными разностям самих давлений и приближенно положить
Порядок выполнения работы
1. Открыть кран Д, при закрытом кране С накачать воздух в баллон так, чтобы разность уровней жидкости в манометре составила 30-40 мм. 2. Закрыть кран Д и выждать 2-3 минуты, пока благодаря теплообмену температура в баллоне не станет равной комнатной, и уровни в коленах манометра перестанут изменяться. 3. Отсчитать разность уровней Н жидкости в коленах манометра. 4. Открыть кран С и в тот момент, когда уровни жидкости обоих коленах манометра сравняются, быстро закрыть кран С. 5. Выждать 2-3 минуты пока газ, охлажденный про адиабатическом расширении, нагреется до комнатной температуры 6. По формуле (8) вычислить значение 7. Опыт повторить 5-7 раз, меняя величину Н.
Все полученные опытом (и вычислением) результаты измерений занести в таблицу отчета.
Таблица
Контрольные вопросы
1. Что называется удельной теплоемкостью? 2. Запишите и сформулируйте I начало термодинамики 3. Почему 4. Какой процесс называется адиабатическим? Запишите уравнение Пуассона. 5. Почему температура газа при адиабатном расширении уменьшается?
V Рис. 2 Литература
1. Шубин А.С. Курс общей физики. 2. Савельев И.В. Курс физики, т.1 3. Детлаф А.А., Яворский Б.М. Курс физики, т.1.
ЛАБОРАТОРНАЯ РАБОТА № 9
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.76 (0.006 с.) |

 (1)
(1) и на работу А, совершаемую системой против внешних сил
и на работу А, совершаемую системой против внешних сил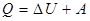 (2)
(2) , следовательно, и А=0. Тогда все подводимое к газу тепло идет на увеличении его внутренней энергии:
, следовательно, и А=0. Тогда все подводимое к газу тепло идет на увеличении его внутренней энергии: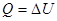
 (3)
(3)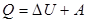 ,
, (4)
(4)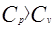 .
.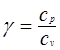 играет в термодинамике весьма важную роль. В частности оно входит в уравнение Пуассона, которое описывает адиабатическое расширение газа
играет в термодинамике весьма важную роль. В частности оно входит в уравнение Пуассона, которое описывает адиабатическое расширение газа (5)
(5) -
-
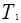 .
.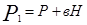 ,
,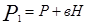 ;
;  и
и 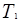
 , а объем будет равен
, а объем будет равен  .
. ,
, 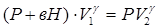 или
или 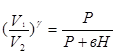 (6).
(6). , давление возрастет до некоторой величины
, давление возрастет до некоторой величины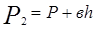 ,
, .
.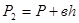 ;
;  ;
; 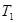
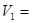 (P+вh)
(P+вh) 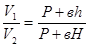
 :
:  (7)
(7)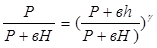
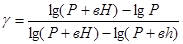
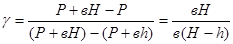
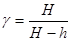 (8)
(8)
 Таким образом, экспериментальное определение
Таким образом, экспериментальное определение 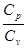 сводится к измерению H и h, то есть формула (8) является расчетной формулой для определения коэффициента
сводится к измерению H и h, то есть формула (8) является расчетной формулой для определения коэффициента 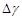
 ?
? P
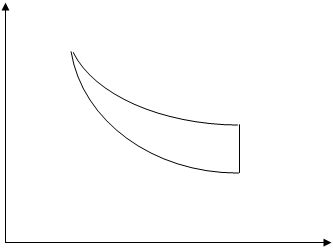
P 1(P
1(P  ,V
,V  3(P
3(P  ,V
,V  2(P,V
2(P,V 


