
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидростатика. Силы действующие в жидкости. Гидростатическое давление в точке и его свойства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гидростатика изучает законы равновесия жидкости и практическое применение этих законов в технике. Силы, действующие в жидкостях: внешние и внутренние. Внутренние силы – это силы взаимодействия между отдельными частицами жидкости. Внешние силы – это силы, приложенные к частицам рассматриваемого объема жидкости со стороны среды, окружающей этот объем. Внешние силы подразделяют на две группы: массовые, поверхностные. Вследствие текучести (подвижности частиц) на жидкость действуют силы не сосредоточенные, а непрерывно распределенные по ее объему (массе) или поверхности. Массовые силы в соответствии со вторым законом Ньютона пропорциональны массе жидкости или для однородной жидкости - ее объему. К ним относятся сила тяжести (вес) где G- сила тяжести (вес) жидкости;m- масса жидкости;g- ускорение силы тяжести; объем жидкости;плотность жидкости; гамма-удельный вес жидкости;Fин- сила инерции; а- ускорение движения. Здесь следует напомнить, что масса является мерой инертности материального тела, в том числе и жидкости. Силы инерции, действующие в жидкостях, так же как и для твердых тел, могут проецироваться на оси координат трехмерного пространства
Гидростатическое давление в точке не зависит от направления, т.е. остается одинаковым по всем направлениям.
Рис. 2.2 Выделим внутри массы жидкости, находящейся в равновесии, малый объем в форме тетраэдра с ребрами dx, dy, dz, соответственно параллельными координатным осям, и с массой dm =
Представим, что жидкость внутри тетраэдра – в виде твердого тела. Это не изменяет условий равновесия. Воспользуемся известными уравнениями статики твердого тела, а именно уравнениями проекций сил и уравнениями моментов:
Учитывая, что при стягивании тетраэдра в точку, уравнения моментов такой системы удовлетворяются тождественно, а действующие на него силы сводятся к системе сил, проходящих через одну и ту же точку.
К действующим силам относятся поверхностные и массовые (объемные) силы. К поверхностным силам относятся силы давления жидкости, окружающей элементарный тетраэдр. Таких сил будет четыре (по числу граней). На грань АВС действует сила
Сила dPx параллельна оси ox, направлена в противоположную сторону оси и, следовательно, войдет в уравнение со знаком «плюс». Силы dPy и dPz,действующие на грани ABD и ACD, соответственно параллельны осям oy и oz и их проекции на ось ox равны нулю. Четвертая сила dPn – сила давления на грань ВСD равна:
Проекция этой силы на ось ox:
Эта сила направлена в отрицательную сторону оси ox. Произведение d wcos(N,ox) представляет собой проекцию площади треугольника BCD на плоскость уoz и равно:
Тогда проекция силы dPn на ось ox численно равна:
Аналогично можно записать проекции силы dPn на оси oy и oz:
Массовые силы, действующие на тетраэдр, приводятся к равнодействующей dR, образующей с координатными осями углы a, b, g и равной:
Обозначим проекции ускорения j по координатным осям x, y, z, т.е. примем, что
Тогда проекции объемной силы dR равны:
Запишем сумму проекций всех сил на ось ox с учетом уравнений (2.12):
Или после сокращения на
Пренебрегая Аналогично py = pn и pz = pn. Следовательно, px = py = pz = pn. (2.14) Что и надо было доказать. Таким образом, гидростатическое давление в точке по любому направлению оказывается одинаковым, т.е. не зависит от направления действия. Поверхностную силу, действующую нормально к какой-либо площадке, называют силой давления
Рис. 2.1. Проведем секущую плоскость а-а, делящую объем W на две части 1 и 2. Отбросим часть 1 и заменим распределенными по площади w силами D р i, одна из которых D р приходится на долю площади Dw. Напряжение сжатия sс, возникающее при этом, определяется как частное от деления силы
Напряжение sс принято называть средним гидростатическим давлением; предел отношения при Dw ® 0 называется гидростатическим давлением в точке:
Единица измерения давления Па.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.82.22 (0.008 с.) |

 и сила инерции
и сила инерции 


 где - проекции силы инерции на оси координат;
где - проекции силы инерции на оси координат;  ,а
,а  - проекции ускорения на оси.
- проекции ускорения на оси. ,
, (2.3)
(2.3) (2.4)
(2.4) , (2.5)
, (2.5) .
.
 , (2.6)
, (2.6) . (2.7)
. (2.7) . (2.8)
. (2.8) . (2.9)
. (2.9) (2.10)
(2.10)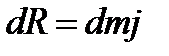 , (2.11)
, (2.11)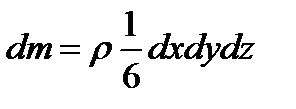 ,
, dxdydz – объем тетраэдра;
dxdydz – объем тетраэдра;
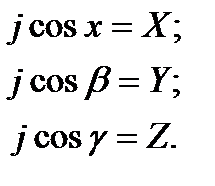
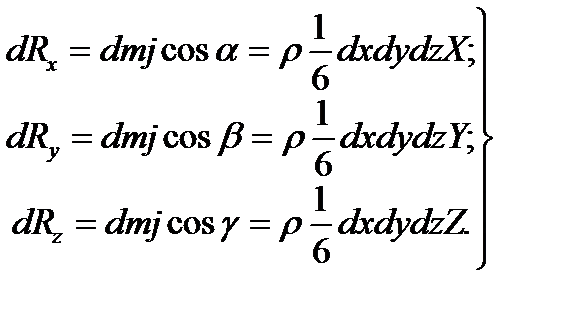 (2.12)
(2.12) . (2.13)
. (2.13)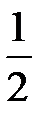 dydz:
dydz: .
.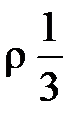 dxX как бесконечно малым относительно px и pn, получаем px – pn = 0 или px = pn.
dxX как бесконечно малым относительно px и pn, получаем px – pn = 0 или px = pn. D р на площадь D:
D р на площадь D: . (2.1)
. (2.1) . (2.2)
. (2.2)


