
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гидростатическое давление и его свойства. Уравнения равновесия жидкостиСодержание книги
Поиск на нашем сайте
Гидростатика — раздел гидравлики, изучающий законы равновесия покоящейся жидкости. Жидкость, находящаяся в покое, подвергается действию внешних сил двух категорий: массовых и поверхностных. К массовым относятся силы, пропорциональные массе жидкости (сила тяжести, сила инерции). К поверхностным относятся силы, распределенные по поверхности, ограничивающей любой мысленно выделенный объем жидкости, и пропорциональные площади этой поверхности (сила давления, центробежная сила).
Рассмотрим некоторый объем покоящейся жидкости (рис. I.2). Мысленно разделим этот объем на две части произвольной плоскостью АВСD и отбросим верхнюю часть. Для сохранения равновесия нижней части к плоскости АВСD необходимо приложить силы, заменяющие действие верхней части объема жидкости на нижнюю.
Рис. 1.3. Схема к доказательству первого свойства гидростатического давления
Возьмем на плоскости АВСD произвольную точку а и выделим около нее малую площадку
В гидравлике силу P называют суммарной силой гидростатического давления, а отношение Если уменьшать площадку
Иначе говоря, гидростатическое давление в точке является пределом отношения силы давления, действующей на элементарную площадку, к ее площади, если она стремится к нулю. Гидростатическое давление измеряется в единицах силы, деленных на единицу площади. В системе СИ за единицу давления принят паскаль (Па) — равномерно распределенное давление, при котором на площадь 1 м2 действует сила 1 Н. Гидростатическое давление обладает двумя свойствами. 1. Гидростатическое давление всегда направлено по внутренней нормали к площадке, на которую оно действует. Это свойство доказывается от противного.
Рассмотрим некоторый объем покоящейся жидкости, внутри которого проведена поверхность КК (рис. 1.3). Возьмем на этой поверхности произвольную точку А. Предположим, что гидростатическое давление в точке А направлено не по нормали, а под углом к поверхности. В этом случае гидростатическое давление р можно разложить на две составляющие: нормальную рп и касательную Гидростатическое давление всегда направлено по внутренней нормали. Если бы оно было направлено по внешней нормали, как это показано на рис. I.3 в точке В, то, поскольку жидкость не оказывает сопротивления растягивающим напряжениям, частицы ее должны были бы прийти в движение, что противоречит принятому условию о нахождении жидкости в покое.
2. Гидростатическое давление в любой точке жидкости действует одинаково по всем направлениям, т. е. не зависит от угла наклона площадки, на которую оно действует. Выделим в объеме жидкости, находящейся в покое, точку А как начало координат и вершину тетраэдра, имеющего грани площадью Кроме сил давления на тетраэдр действует сила тяжести G, проекция которой на ось х, а также на ось у равна нулю, а на ось z составляет Тетраэдр будет находиться в покое, если суммы проекций все-: действующих сил на оси координат будут равны нулю. Уравнение равновесия по оси х будет иметь следующий вид:
аналогичны уравнения равновесия по осям у и z. Проекции площади Если сделать замену, то уравнение равновесия по оси х будет иметь следующий вид:
аналогичны уравнения равновесия по осям у и z.
После сокращения получим рх = рп; ру = рn; рz = рп или
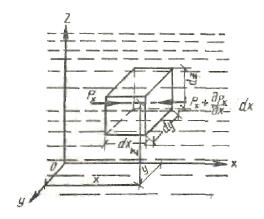
Это равенство доказывает второе свойство гидростатического давления. Для вывода уравнений равновесия жидкости выделим в покоящейся жидкости бесконечно малый прямоугольный параллелепипед с ребрами dх, dу и dz (рис. 1.5). На параллелепипед действуют силы гидростатического давления и массовые силы. На грани площадью dуdz будут действовать средние гидростатические давления px и где py и Равнодействующую массовых сил обозначим G, а ее проекции на координатные оси, отнесенные к единице массы, обозначим X, У и Z. Сумма проекций всех сил на ось х имеет вид:
Проекции на оси у и z имеют аналогичный вид. После преобразования запишем: — дрх/дх + Хρ = 0, а разделив обе части равенства на плотность жидкости ρ, получим уравнения равновесия жидкости в общем виде:
Эти уравнения выражают закон распределения гидростатического давления. Приведем их к виду, удобному для интегрирования. Умножив каждое соответственно на dх, dу и dz и сложив вместе, получим:
Выражение в скобках есть полный дифференциал гидростатического давления р, т. е.
При ρ = const правая часть уравнения является тоже полным дифференциалом функции U=f(x,y,z), частные производные которой будут Если в выражение (1.6) подставить значения X, У и Z, то получим
Интегрируя это уравнение, запишем
где С — постоянная интегрирования. Если известны давление р0 и потенциальная функция U0 для точки жидкости, то уравнение принимает вид:
Из уравнений (1.6а) и (1.6б) находим
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.49.66 (0.007 с.) |


 Под действием внешних сил в каждой точке жидкости возникают внутренние силы, характеризующие ее напряженное состояние (давление в точке).
Под действием внешних сил в каждой точке жидкости возникают внутренние силы, характеризующие ее напряженное состояние (давление в точке).

 . В центре этой площадки действует сила P, представляющая собой равнодействующую сил, приложенных к различным точкам площадки
. В центре этой площадки действует сила P, представляющая собой равнодействующую сил, приложенных к различным точкам площадки 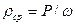 (I.3)
(I.3) — средним гидростатическим давлением.
— средним гидростатическим давлением. . (I.4)
. (I.4) к поверхности КК- Однако, если бы существовала касательная составляющая гидростатического давления
к поверхности КК- Однако, если бы существовала касательная составляющая гидростатического давления  то частицы жидкости вышли бы из равновесия и жидкость не находилась бы в покое. Следовательно, касательная составляющая
то частицы жидкости вышли бы из равновесия и жидкость не находилась бы в покое. Следовательно, касательная составляющая 
 ,
,  ,
,  и
и  (рис. I.4). На грани тетраэдра действуют силы гидростатического давления
(рис. I.4). На грани тетраэдра действуют силы гидростатического давления  ,
, 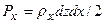 ,
,  и
и  , где
, где  ,
,  ,
,  ; и
; и  — средние гидростатические давления, действующие на грани.
— средние гидростатические давления, действующие на грани. , т. е. очень мала и ею можно пренебречь.
, т. е. очень мала и ею можно пренебречь.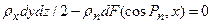 ;
; ;
;  ;
;  .
. ;
;
 (I.5)
(I.5)
 — частная производная рх по х, характеризующая изменение давления на единицу длины в направлении оси х, т. е. приращение среднего давления рх на длине dх. На другие грани, по аналогии, будут действовать средние гидростатические давления:
— частная производная рх по х, характеризующая изменение давления на единицу длины в направлении оси х, т. е. приращение среднего давления рх на длине dх. На другие грани, по аналогии, будут действовать средние гидростатические давления: pz и
pz и 



 (1.6)
(1.6)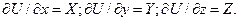 Функцию U называют потенциалом сил, необходимым для сохранения равновесия жидкости. Силами, имеющими потенциал, являются сила инерции и сила тяжести.
Функцию U называют потенциалом сил, необходимым для сохранения равновесия жидкости. Силами, имеющими потенциал, являются сила инерции и сила тяжести. или
или 
 , (1.6а)
, (1.6а) (1.6б)
(1.6б) (1.7)
(1.7)


