
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткий обзор развития гидравликиСодержание книги
Поиск на нашем сайте
В. И. Калицун, В.С.Кедров, Ю.М.Ласков, П.В.Сафонов ГИДРАВЛИКА, ВОДОСНАБЖЕНИЕ И КАНАЛИЗАЦИЯ Издание третье, переработанное и дополненное Допущено Министерством высшего и среднего специального образования СССР в качестве учебника для студентов вузов, обучающихся по специальности «Промышленное и гражданское строительство» МОСКВА СТРОЙИЗДАТ Оглавление Раздел I. ГИДРАВЛИКА... 4 Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.. 4 § 1. КРАТКИЙ ОБЗОР РАЗВИТИЯ ГИДРАВЛИКИ.. 4 § 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ.. 4 Глава 2. ГИДРОСТАТИКА.. 6 § 3. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ И ЕГО СВОЙСТВА. УРАВНЕНИЯ РАВНОВЕСИЯ ЖИДКОСТИ.. 6 § 4. ПОВЕРХНОСТИ РАВНОГО ДАВЛЕНИЯ. СВОБОДНАЯ ПОВЕРХНОСТЬ.. 10 § 5. ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ. ЗАКОН ПАСКАЛЯ.. 10 § 6. АБСОЛЮТНОЕ И МАНОМЕТРИЧЕСКОЕ ДАВЛЕНИЕ. ПЬЕЗОМЕТРИЧЕСКАЯ ВЫСОТА. ВАКУУМ... 11 § 7. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ.. 12 § 8. ГИДРАВЛИЧЕСКИЕ МАШИНЫ ГИДРОСТАТИЧЕСКОГО ДЕЙСТВИЯ.. 13 Глава 3. ДАВЛЕНИЕ ЖИДКОСТИ НА ПЛОСКИЕ И КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ.. 14 § 9. ДАВЛЕНИЕ ЖИДКОСТИ НА ПЛОСКИЕ ПОВЕРХНОСТИ. ЦЕНТР ДАВЛЕНИЯ. ЭПЮРА ДАВЛЕНИЯ 14 § 10. ДАВЛЕНИЕ ЖИДКОСТИ НА КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ.. 17 § 11. ПЛАВАНИЕ ТЕЛ В ЖИДКОСТИ. ЗАКОН АРХИМЕДА.. 18 Глава 4. ОСНОВНЫЕ ПОНЯТИЯ ГИДРОДИНАМИКИ.. 19 § 12. ВИДЫ ДВИЖЕНИЯ ЖИДКОСТИ. ЛИНИЯ ТОКА. ЭЛЕМЕНТАРНАЯ СТРУЙКА И ПОТОК.. 19 § 13. ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОТОКА. РАВНОМЕРНОЕ И НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ. НАПОРНЫЙ И БЕЗНАПОРНЫЙ ПОТОК.. 20 Глава 5. УРАВНЕНИЯ ДВИЖЕНИЯ ЖИДКОСТИ.. 21 § 14. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ ПОТОКА.. 21 § 15. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ПОТОКА ЖИДКОСТИ. ГЕОМЕТРИЧЕСКОЕ И ЭНЕРГЕТИЧЕСКОЕ ТОЛКОВАНИЕ УРАВНЕНИЯ БЕРНУЛЛИ.. 22 § 16. ПРАКТИЧЕСКОЕ ПРИЛОЖЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ.. 26 § 17. УРАВНЕНИЕ РАВНОМЕРНОГО ДВИЖЕНИЯ ЖИДКОСТИ.. 27 Глава 6. ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ.. 27 § 18. ВИДЫ СОПРОТИВЛЕНИЙ (ПОТЕРЬ НАПОРА) 27 § 19. ДВА РЕЖИМА ДВИЖЕНИЯ ЖИДКОСТИ.. 28 § 20. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ПОТЕРИ НАПОРА ПРИ ЛАМИНАРНОМ РЕЖИМЕ ДВИЖЕНИЯ ЖИДКОСТИ В ТРУБАХ.. 29 § 21. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ ПРИ ТУРБУЛЕНТНОМ РЕЖИМЕ ДВИЖЕНИЯ ЖИДКОСТИ В ТРУБАХ 30 § 22. ОПРЕДЕЛЕНИЕ ПОТЕРЬ НАПОРА ПО ДЛИНЕ.. 31 § 23. ПОТЕРИ НАПОРА В МЕСТНЫХ СОПРОТИВЛЕНИЯХ.. 35 § 24. ОБЩИЕ ПОТЕРИ НАПОРА.. 40 Глава 7. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, ЧЕРЕЗ НАСАДКИ И ВОДОСЛИВЫ... 41 § 25. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ МАЛОГО ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ ПРИ ПОСТОЯННОМ НАПОРЕ 41 § 26. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ МАЛОГО ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ ПРИ ПЕРЕМЕННОМ НАПОРЕ 43 § 27. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ НАСАДКИ.. 45 § 28. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ВОДОСЛИВЫ... 47 Глава 8. РАСЧЕТ НАПОРНЫХ ТРУБОПРОВОДОВ.. 49 § 29. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ ТРУБОПРОВОДОВ.. 49 § 30. ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ ГИДРАВЛИЧЕСКОГО РАСЧЕТА ТРУБОПРОВОДОВ.. 49 § 31. ОСНОВЫ РАСЧЕТА ПРОСТЫХ КОРОТКИХ И ДЛИННЫХ ТРУБОПРОВОДОВ.. 54 § 32. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ТРУБОПРОВОДОВ.. 56 § 33. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ТРУБОПРОВОДОВ.. 57 § 34. ОСНОВЫ РАСЧЕТА ТРУБОПРОВОДОВ ПРИ РАВНОМЕРНОЙ РАЗДАЧЕ РАСХОДА ПО ПУТИ.. 58 § 35. ГИДРОТРАНСПОРТ.. 59 § 36. ГИДРАВЛИЧЕСКИЙ УДАР В ТРУБАХ.. 60 Глава 9. РАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ.. 63 § 37. ОСОБЕННОСТИ ДВИЖЕНИЯ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ. РАСЧЕТНАЯ ФОРМУЛА.. 63 § 38. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ШЕЗИ С.. 64 § 39. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ ПО СЕЧЕНИЮ ПОТОКА. ДОПУСТИМЫЕ СКОРОСТИ ДВИЖЕНИЯ 65 § 40. ГИДРАВЛИЧЕСКИ НАИВЫГОДНЕЙШЕЕ СЕЧЕНИЕ КАНАЛА.. 67 § 41. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ КАНАЛОВ.. 68 § 42. ОСОБЕННОСТИ ГИДРАВЛИЧЕСКОГО РАСЧЕТА БЕЗНАПОРНЫХ ТРУБ.. 70 Глава 10. ДВИЖЕНИЕ ГРУНТОВЫХ ВОД.. 72 § 43. ВИДЫ ДВИЖЕНИЯ ВОДЫ В ГРУНТАХ.. 72 § 44. ЗАКОН ФИЛЬТРАЦИИ.. 72 § 45. ПРИТОК ГРУНТОВЫХ ВОД К СКВАЖИНАМ... 74
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ КРАТКИЙ ОБЗОР РАЗВИТИЯ ГИДРАВЛИКИ Гидравлика — наука, изучающая законы равновесия и движения жидкостей и рассматривающая способы приложения этих законов к решению конкретных практических задач. Гидравлика составляет основу многих инженерных расчетов при конструировании специальных сооружений (плотин, сетей, отстойников, фильтров и т. п.). Начало развития гидравлики относится к античному периоду. Еще за 250 лет до н. э. появился трактат Архимеда «О плавающих телах», где был сформулирован закон о воздействии воды на погруженное в нее тело. Особое развитие гидравлика как наука получила в XV—XVII вв. Леонардо да Винчи (1452—1519 гг.) написал труд «О движении и измерении воды». В 1612 г. Г. Галилей теоретически подтвердил закон Архимеда. В 1643 г. Э. Торричелли установил закон истечения жидкости из отверстия. В 1650 г. Б. Паскаль сформулировал закон о передаче жидкостью давления. В 1687 г. И. Ньютон предложил гипотезу о законе внутреннего трения в движущейся жидкости и дал понятие о вязкости жидкости. Дальнейшее развитие гидравлики связано с именами русских ученых — М. В. Ломоносова, Д. Бернулли и Л. Эйлера, установивших основные законы гидродинамики. Инженерное применение теоретических основ гидродинамики получило отражение в работах таких ученых, как А. Шези (движение жидкости в каналах и трубах). Д. Вентури (истечение из отверстий), Дарси (напорное движение воды в трубах), О. Рейнольдc (режимы движения жидкостей в трубах) и др. Широко известны работы Н. Е. Жуковского (1847—1921 гг.), создавшего теорию гидравлического удара в водопроводе, Н. П. Петрова (1836—1920 гг.), разработавшего гидродинамическую теорию смазки, и И. С. Громека (1851 —1889 гг.), получившего уравнения вихревого движения жидкости. Большой вклад в развитие гидравлики внесли советские ученые: Н. Н. Павловский, А. Н. Колмогоров, С. А. Христианович, М. А. Великанов, А. Я Милович и многие другие. Гидравлика как прикладная инженерная наука необходима для расчетов при проектировании сети и сооружений систем водоснабжения, канализации, осушения и орошения, гидротехнических со оружений, мостов, для расчета транспортирования строительных растворов по трубам, конструирования насосов, компрессоров и т. п. Глава 2. ГИДРОСТАТИКА Глава 3. ДАВЛЕНИЕ ЖИДКОСТИ НА ПЛОСКИЕ И КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ Глава 4. ОСНОВНЫЕ ПОНЯТИЯ ГИДРОДИНАМИКИ Глава 5. УРАВНЕНИЯ ДВИЖЕНИЯ ЖИДКОСТИ ПРАКТИЧЕСКОЕ ПРИЛОЖЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ На основании уравнения Бернулли сконструирован ряд приборов, таких как водомер Вентури, водоструйный насос, эжектор и пр. На рис. 1.24 показан горизонтальный трубопровод диаметром D, на котором устроено сужение диаметром d. В нормальной и суженной частях установлены два пьезометра (в сечениях /—/ и //—//).
Ж
Рис. 1.24. Схема водомера Вентури Пренебрегая потерями напора между сечениями I—I и II—II, а также неравномерностью распределения скоростей по сечению (a = 1) и принимая, что плоскость сравнения 00 проходит через ось трубопровода, можем записать уравнение Бернулли в таком виде:
Отсюда следует, что с увеличением скорости движения давление должно уменьшаться и, наоборот, с уменьшением скорости давление должно увеличиваться. Это положение используется в водомере Вентури, где по разности показаний пьезометров h (см. рис. 1.24), зная диаметры D и d, можно определить расход. В водоструйном насосе (рис. 1.25) вода из бака I поступает в трубопровод, имеющий сужение. В узком сечении скорость струи возрастает, и. струя увлекает за собой воздух, находящийся в смесительной камере, благодаря чему происходит подсасывание жидкости по трубке, опущенной в бак 2. При больших скоростях движения жидкость будет подсасываться из бака 2 непрерывно. По этому же принципу работают эжекторы и гидроэлеваторы. ВИДЫ СОПРОТИВЛЕНИЙ (ПОТЕРЬ НАПОРА) Решение многих практических задач гидравлики сводится к установлению зависимости, определяющей изменение скорости и давления по длине потока. Для этого могут быть использованы: уравнение постоянства расхода
и уравнение Бернулли
Эти уравнения обычно имеют три неизвестных: υ, р и hпот, поэтому для их решения необходимо третье уравнение. В качестве третьего уравнения используют зависимость потерь напора от скорости υ и ряда других факторов. Потери напора (энергии) потока вызываются сопротивлениями двух видов: 1) сопротивлениями по длине, обусловленными силами трения; 2) местными сопротивлениями, обусловленными изменениями скорости потока по величине и направлению. Потери напора по длине трубопровода обычно определяют по формуле Дарси—Вейсбаха
а местные потери — по формуле Вейсбаха
где λ — коэффициент гидравлического трения (коэффициент Дарси); l — длина трубопровода; d — диаметр трубопровода; υ — средняя скорость потока за местным сопротивлением; ξ — коэффициент местного сопротивления. Коэффициенты λ и ξ безразмерны. Экспериментальные исследования показали, что эти коэффициенты зависят от многих факторов, в частности, от режима движения и шероховатости стенок. Рис.1.31. График Г.А. Мурина шероховатостью. Таким образом, на графике дана зависимость коэффициента λ от числа Рейнольдса и относительной шероховатости. На графике можно выделить три области: 1 — область гидравлически гладких труб, соответствующую сравнительно малым числам Рейнольдса; 2 — область вполне шероховатого трения (область квадратичного закона), соответствующую сравнительно большим числам Рейнольдса; 3 — переходную область между ними. В области гидравлически гладких труб коэффициент λ зависит только от числа Рейнольдса. В переходной области коэффициент λ зависит от числа Рейнольдса и относительной шероховатости. В области квадратичного сопротивления коэффициент % зависит только от относительной шероховатости. Полуэмпирическая теория турбулентности дает следующее объяснение приведенным закономерностям изменения коэффициента λ. Толщина ламинарного слоя, расположенного у стенки русла, изменяется в зависимости от числа Рейнольдса. С уменьшением числа Рейнольдса толщина ламинарного слоя увеличивается, а с увеличением числа Рейнольдса она уменьшается. В области гидравлически гладких труб, соответствующей сравнительно малым числам Рейнольдса, выступы шероховатости стенок русел полностью находятся в ламинарном слое и по существу не оказывают сопротивления движению жидкости. В этой области сопротивление движению обусловливается только внутренними сопротивлениями, вызванными турбулентным перемешиванием. В области квадратичного сопротивления, соответствующей большим числам Рейнольдса, вследствие относительно малой толщины ламинарного слоя выступы шероховатости стенок русел попадают в ядро течения и оказывают дополнительное сопротивление движению жидкости. В переходной области выступы шероховатости стенок русел частично находятся в ламинарном слое, а частично попадают в ядро течения. В этой области сопротивления движению жидкости, обусловленные внутренними сопротивлениями и шероховатостью стенох русел, соизмеримы. Для опреде-"' я коэффициента гидравлического трения λ при
Для области гидравлически гладких труб она преобразуется в формулу Прандтля:
Таблица 1.1. Рекомендуемые значения эквивалентной шероховатости k9 для труб из различных материалов
а для области квадратичного сопротивления — в формулу Никурадзе: 1/ Для расчета трубопроводов различного назначения (тепловых сетей, газопроводов и т. д.) можно применять формулу А. Д. Альтшуля:
Для области гидравлически гладких труб она принимает более простой вид, практически совпадающий с широко известной формулой Блазиуса:
а для области квадратичного сопротивления она приводится к формуле Шифринсона:
При практических расчетах значения эквивалентной шероховатости принимают с учетом материала стенок русла и их состояния, зависящего, в частности, от продолжительности и условий эксплуатации (табл. 1.1). Расчет водопроводных сетей из стальных и чугунных труб, бывших в эксплуатации, обычно проводят по формулам Ф. А. Шевелева: при v < 1,2 м/с (в переходной области)
при
Для нахождения коэффициента λ при расчете трубопроводов из других материалов или трубопроводов, предназначенных для транспортирования жидкостей, отличающихся от воды, применяют другие эмпирические формулы. Потери напора в трубах некруглого сечения, а также при безнапорном движении можно определять по формуле Дарси—Вейсбаха:
Эта зависимость получена из формулы (1.55) путем замены диаметра d гидравлическим радиусом R, равным R = d/4. (I-77) Возможность подобного преобразования формулы (1.55) подтверждается хорошим согласованием зависимости (1.76) с опытными данными. Коэффициент гидравлического трения λ в этой зависимости вычисляют по приведенным выше выражениям с учетом формулы (1.77). ОБЩИЕ ПОТЕРИ НАПОРА Общие потери напора определяют путем арифметического суммирования потерь напора по длине и потерь, вызванных отдельными местными сопротивлениями: hпот= Этот метод определения потерь напора получил название принципа наложения потерь. Таким образом, в трубопроводе постоянного диаметра общие потери напора равны:
или
Если обозначить
Метод наложения потерь напора применим только в том случае, если перед местными сопротивлениями поток успевает стабилизироваться, т. е. кривая распределения скоростей приобретает нормальный вид, соответствующий равномерному движению воды. Длина стабилизирующего прямолинейного участка составляет от 10 до 30 d, где d — диаметр трубопровода. При близком расположении местных сопротивлений друг от друга принцип наложения потерь напора дает ошибочные результаты. В этом случае потери напора следует определять экспериментально. ГИДРОТРАНСПОРТ Транспортирование смеси воды и твердых веществ (пульпы), например цементного раствора, красителей и т. п., по трубам, лоткам, желобам, каналам называется гидротранспортом. Основными характеристиками гидросмеси (пульпы) являются консистенция (количество твердых частиц в единице объема жидкости) и крупность частиц. Консистенция может быть выражена массовой концентрацией, т. е. содержанием частиц по массе в процентах к массе жидкости. Скорость выпадения твердых частиц в жидкости называют гидравлической крупностью. При турбулентном режиме потока гидросмеси в трубах твердые частицы не оседают на дно, а перемещаются во взвешенном состоянии благодаря наличию подъемной силы, пропорциональной квадрату скорости потока. Наименьшая скорость потока гидросмеси, при которой не образуется осадка, называется критической. Критическая скорость зависит от крупности частиц, их удельного веса, консистенции гидросмеси и диаметра трубопровода. Для напорных пульпопроводов критическую скорость можно определить по формуле В. С. Кнороза:
где ωч — гидравлическая крупность частиц средним диаметром d0; р — массовая концентрация гидросмеси; d — диаметр трубопровода Аналогично гидротранспорту работает пневматический транспорт — перемещение смеси сыпучих материалов с воздухом по трубам. Скорость перемещения смеси должна быть больше критической скорости витания частиц. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ШЕЗИ С Коэффициент Шези С, входящий в основные расчетные формулы равномерного движения в открытых руслах, можно определять по ряду эмпирических формул. Широкое распространение для определения коэффициента Шези С получила формула Н. Н. Павловского
Таблица 1.7. Значения коэффициента шероховатости п в формуле Н. Н. Павловского
Формула (1.136) основана на большом опытном материале и хорошо подтверждается на практике. В ряде случаев для подсчета коэффициента Шези С применяют формулу Маннинга:
При расчете ирригационных каналов рекомендуется пользоваться формулой И. И. Агроскина:
Расчет каналов и лотков, имеющих сравнительно гладкие стенки, рекомендуется производить по формуле А. Д. Альтшуля
Таблица 1,8. Значения приведенной линейной шероховатости ε
Характеристика русла
Исключительно гладкие поверхности (эмалированные, глазурованные и т. д.)....... Чистая цементная штукатурка................. Металлические лотки гладкие..................... Деревянные лотки, бетонировка................. Кирпичная кладка....................................... Тесаный камень..........................................
где R — гидравлический радиус, мм; ε — приведенная линейная шероховатость; мм (табл 1.8) Формула (1.140) представляет собой обобщенную зависимость, справедливую для всей области турбулентного режима движения. ЗАКОН ФИЛЬТРАЦИИ Закон фильтрации был установлен Дарси в 1856 г. на основании результатов проведенных им экспериментов с песчаным грунтом при изменении пьезометрических уклонов от 1,5 до 18. Позднее этот закон получил и теоретическое подтверждение. Закон Дарси может быть выражен формулой
где υ — скорость фильтрации; к ф — коэффициент фильтрации, характеризующий фильтрационную способность грунта; обычно значение к фопределяют опытным путем; J — гидравлический градиент грунтового потока (пьезометрический уклон). Из рассмотрения зависимости (1.157) можно заключить, что коэффициент фильтрации представляет собой скорость фильтрации при единичном уклоне. Расход фильтрационного потока может быть выражен такой зависимостью Q = где ω — площадь живого сечения, нормального к направлению движения. В 1857 г. французский ученый Дюпюи, основываясь на законе Дарси и дав этому закону некоторое теоретическое обоснование, рассмотрел случай движения фильтрационного потока со свободной поверхностью при горизонтальном подстилающем слое и получил известное уравнение кривой депрессии (рис. 1.54):
где q — расход грунтового потока, приходящийся на единицу его ширины; h1, и h2 — глубины грунтового потока в сечениях I—I и II—II; l — горизонтальное расстояние между сечениями I—I и II—II.
Рис. 1.54. Схема к выводу уравнения кривой депрессии
Зависимости (1.157) —(1.159) позволяют решать многие практические задачи, связанные с фильтрацией в водопроницаемых грунтах. В последующем изложении будет показано несколько случаев использования указанных формул. В. И. Калицун, В.С.Кедров, Ю.М.Ласков, П.В.Сафонов ГИДРАВЛИКА, ВОДОСНАБЖЕНИЕ И КАНАЛИЗАЦИЯ Издание третье, переработанное и дополненное Допущено Министерством высшего и среднего специального образования СССР в качестве учебника для студентов вузов, обучающихся по специальности «Промышленное и гражданское строительство» МОСКВА СТРОЙИЗДАТ Оглавление Раздел I. ГИДРАВЛИКА... 4 Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.. 4 § 1. КРАТКИЙ ОБЗОР РАЗВИТИЯ ГИДРАВЛИКИ.. 4 § 2. ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ.. 4 Глава 2. ГИДРОСТАТИКА.. 6 § 3. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ И ЕГО СВОЙСТВА. УРАВНЕНИЯ РАВНОВЕСИЯ ЖИДКОСТИ.. 6 § 4. ПОВЕРХНОСТИ РАВНОГО ДАВЛЕНИЯ. СВОБОДНАЯ ПОВЕРХНОСТЬ.. 10 § 5. ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ. ЗАКОН ПАСКАЛЯ.. 10 § 6. АБСОЛЮТНОЕ И МАНОМЕТРИЧЕСКОЕ ДАВЛЕНИЕ. ПЬЕЗОМЕТРИЧЕСКАЯ ВЫСОТА. ВАКУУМ... 11 § 7. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЯ.. 12 § 8. ГИДРАВЛИЧЕСКИЕ МАШИНЫ ГИДРОСТАТИЧЕСКОГО ДЕЙСТВИЯ.. 13 Глава 3. ДАВЛЕНИЕ ЖИДКОСТИ НА ПЛОСКИЕ И КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ.. 14 § 9. ДАВЛЕНИЕ ЖИДКОСТИ НА ПЛОСКИЕ ПОВЕРХНОСТИ. ЦЕНТР ДАВЛЕНИЯ. ЭПЮРА ДАВЛЕНИЯ 14 § 10. ДАВЛЕНИЕ ЖИДКОСТИ НА КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ.. 17 § 11. ПЛАВАНИЕ ТЕЛ В ЖИДКОСТИ. ЗАКОН АРХИМЕДА.. 18 Глава 4. ОСНОВНЫЕ ПОНЯТИЯ ГИДРОДИНАМИКИ.. 19 § 12. ВИДЫ ДВИЖЕНИЯ ЖИДКОСТИ. ЛИНИЯ ТОКА. ЭЛЕМЕНТАРНАЯ СТРУЙКА И ПОТОК.. 19 § 13. ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОТОКА. РАВНОМЕРНОЕ И НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ. НАПОРНЫЙ И БЕЗНАПОРНЫЙ ПОТОК.. 20 Глава 5. УРАВНЕНИЯ ДВИЖЕНИЯ ЖИДКОСТИ.. 21 § 14. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ ПОТОКА.. 21 § 15. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ПОТОКА ЖИДКОСТИ. ГЕОМЕТРИЧЕСКОЕ И ЭНЕРГЕТИЧЕСКОЕ ТОЛКОВАНИЕ УРАВНЕНИЯ БЕРНУЛЛИ.. 22 § 16. ПРАКТИЧЕСКОЕ ПРИЛОЖЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ.. 26 § 17. УРАВНЕНИЕ РАВНОМЕРНОГО ДВИЖЕНИЯ ЖИДКОСТИ.. 27 Глава 6. ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ.. 27 § 18. ВИДЫ СОПРОТИВЛЕНИЙ (ПОТЕРЬ НАПОРА) 27 § 19. ДВА РЕЖИМА ДВИЖЕНИЯ ЖИДКОСТИ.. 28 § 20. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ И ПОТЕРИ НАПОРА ПРИ ЛАМИНАРНОМ РЕЖИМЕ ДВИЖЕНИЯ ЖИДКОСТИ В ТРУБАХ.. 29 § 21. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ ПРИ ТУРБУЛЕНТНОМ РЕЖИМЕ ДВИЖЕНИЯ ЖИДКОСТИ В ТРУБАХ 30 § 22. ОПРЕДЕЛЕНИЕ ПОТЕРЬ НАПОРА ПО ДЛИНЕ.. 31 § 23. ПОТЕРИ НАПОРА В МЕСТНЫХ СОПРОТИВЛЕНИЯХ.. 35 § 24. ОБЩИЕ ПОТЕРИ НАПОРА.. 40 Глава 7. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ, ЧЕРЕЗ НАСАДКИ И ВОДОСЛИВЫ... 41 § 25. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ МАЛОГО ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ ПРИ ПОСТОЯННОМ НАПОРЕ 41 § 26. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ МАЛОГО ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ ПРИ ПЕРЕМЕННОМ НАПОРЕ 43 § 27. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ НАСАДКИ.. 45 § 28. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ВОДОСЛИВЫ... 47 Глава 8. РАСЧЕТ НАПОРНЫХ ТРУБОПРОВОДОВ.. 49 § 29. НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ ТРУБОПРОВОДОВ.. 49 § 30. ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ ГИДРАВЛИЧЕСКОГО РАСЧЕТА ТРУБОПРОВОДОВ.. 49 § 31. ОСНОВЫ РАСЧЕТА ПРОСТЫХ КОРОТКИХ И ДЛИННЫХ ТРУБОПРОВОДОВ.. 54 § 32. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ТРУБОПРОВОДОВ.. 56 § 33. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ТРУБОПРОВОДОВ.. 57 § 34. ОСНОВЫ РАСЧЕТА ТРУБОПРОВОДОВ ПРИ РАВНОМЕРНОЙ РАЗДАЧЕ РАСХОДА ПО ПУТИ.. 58 § 35. ГИДРОТРАНСПОРТ.. 59 § 36. ГИДРАВЛИЧЕСКИЙ УДАР В ТРУБАХ.. 60 Глава 9. РАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ.. 63 § 37. ОСОБЕННОСТИ ДВИЖЕНИЯ ЖИДКОСТИ В ОТКРЫТЫХ РУСЛАХ. РАСЧЕТНАЯ ФОРМУЛА.. 63 § 38. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ШЕЗИ С.. 64 § 39. РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ ПО СЕЧЕНИЮ ПОТОКА. ДОПУСТИМЫЕ СКОРОСТИ ДВИЖЕНИЯ 65 § 40. ГИДРАВЛИЧЕСКИ НАИВЫГОДНЕЙШЕЕ СЕЧЕНИЕ КАНАЛА.. 67 § 41. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ КАНАЛОВ.. 68 § 42. ОСОБЕННОСТИ ГИДРАВЛИЧЕСКОГО РАСЧЕТА БЕЗНАПОРНЫХ ТРУБ.. 70 Глава 10. ДВИЖЕНИЕ ГРУНТОВЫХ ВОД.. 72 § 43. ВИДЫ ДВИЖЕНИЯ ВОДЫ В ГРУНТАХ.. 72 § 44. ЗАКОН ФИЛЬТРАЦИИ.. 72 § 45. ПРИТОК ГРУНТОВЫХ ВОД К СКВАЖИНАМ... 74
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ КРАТКИЙ ОБЗОР РАЗВИТИЯ ГИДРАВЛИКИ Гидравлика — наука, изучающая законы равновесия и движения жидкостей и рассматривающая способы приложения этих законов к решению конкретных практических задач. Гидравлика составляет основу многих инженерных расчетов при конструировании специальных сооружений (плотин, сетей, отстойников, фильтров и т. п.). Начало развития гидравлики относится к античному периоду. Еще за 250 лет до н. э. появился трактат Архимеда «О плавающих телах», где был сформулирован закон о воздействии воды на погруженное в нее тело. Особое развитие гидравлика как наука получила в XV—XVII вв. Леонардо да Винчи (1452—1519 гг.) написал труд «О движении и измерении воды». В 1612 г. Г. Галилей теоретически подтвердил закон Архимеда. В 1643 г. Э. Торричелли установил закон истечения жидкости из отверстия. В 1650 г. Б. Паскаль сформулировал закон о передаче жидкостью давления. В 1687 г. И. Ньютон предложил гипотезу о законе внутреннего трения в движущейся жидкости и дал понятие о вязкости жидкости. Дальнейшее развитие гидравлики связано с именами русских ученых — М. В. Ломоносова, Д. Бернулли и Л. Эйлера, установивших основные законы гидродинамики. Инженерное применение теоретических основ гидродинамики получило отражение в работах таких ученых, как А. Шези (движение жидкости в каналах и трубах). Д. Вентури (истечение из отверстий), Дарси (напорное движение воды в трубах), О. Рейнольдc (режимы движения жидкостей в трубах) и др. Широко известны работы Н. Е. Жуковского (1847—1921 гг.), создавшего теорию гидравлического удара в водопроводе, Н. П. Петрова (1836—1920 гг.), разработавшего гидродинамическую теорию смазки, и И. С. Громека (1851 —1889 гг.), получившего уравнения вихревого движения жидкости. Большой вклад в развитие гидравлики внесли советские ученые: Н. Н. Павловский, А. Н. Колмогоров, С. А. Христианович, М. А. Великанов, А. Я Милович и многие другие. Гидравлика как прикладная инженерная наука необходима для расчетов при проектировании сети и сооружений систем водоснабжения, канализации, осушения и орошения, гидротехнических со оружений, мостов, для расчета транспортирования строительных растворов по трубам, конструирования насосов, компрессоров и т. п.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 778; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.240.171 (0.031 с.) |



 . (1.48)
. (1.48)
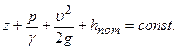
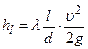 , (1.55)
, (1.55) (1.56)
(1.56)

 Новые
Новые
 Новые или старые в хорошем состоянии;
Новые или старые в хорошем состоянии;
 эксплуатации в воде, но не коррозированы
эксплуатации в воде, но не коррозированы

 = 2lg r/kэ:,+ 1,74. (1.70)
= 2lg r/kэ:,+ 1,74. (1.70) (1.71)
(1.71) (1.72)
(1.72) (1.73)
(1.73) ; (1.74)
; (1.74) м/с (в области квадратичного сопротивления:
м/с (в области квадратичного сопротивления: (1.75)
(1.75) (1.76)
(1.76)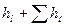 (1.86)
(1.86) (1.87)
(1.87)
 через ζ l, получим:
через ζ l, получим: (1.89)
(1.89)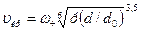 (1-126)
(1-126)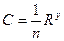 (1.136)
где n—коэффициент шероховатости (табл. 1.7); R — гидравлический радиус, и; у — показатель степени, определяемый по формуле
(1.136)
где n—коэффициент шероховатости (табл. 1.7); R — гидравлический радиус, и; у — показатель степени, определяемый по формуле
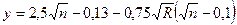 (1.137)
(1.137)
 . (1.138)
. (1.138)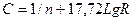 (1.139)
(1.139)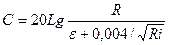 (1.140)
(1.140) (1-157)
(1-157) , (I.158)
, (I.158) (1.159)
(1.159)




