
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Бернулли для потока жидкости. Геометрическое и энергетическое толкование уравнения БернуллиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение Бернулли для потока жидкости. Рассмотрим поток жидкости с плавно изменяющимся движением (рис. 1.21). Выберем два произвольных сечения I—I и II—II, нормальных к оси потока, и рассмотрим заключенный между ними участок потока. Обозначим средние скорости потока в этих сечениях υ1 и υ2; площади живых сечений ω1 и ω 2; гидродинамические давления в центре тяжести этих сечений р1 и р2, расстояния от произвольно выбранной горизонтальной плоскости OO, называемой плоскостью сравнения, до центров тяжести сечений z1 и z2. Применим к участку потока, заключенному между сечениями I—I и II—II, закон сохранения энергии. За время ∆t частицы из сечения I—I перейдут в положение I' — I', а из сечения II—II в положение II'—II'. При этом будут пройдены пути υ1∆t и υ2∆t Через сечение I—I в рассматриваемый участок за время ∆t войдет объем жидкости Q1∆t, за это же время из этого участка через сечение II—II выйдет объем жидкости Q2∆t Найдем количество энергии, внесенной потоком в рассматриваемый участок за время ∆t через сечение I—I. Объем жидкости Q1∆t обладает массой
Рис. 1.21. Схема к выводу уравнения Бернулли а кинетическая энергия этого же объема
Совершенно очевидно, что выражение (1.42) будет представлять собой потенциальную энергию давления рассматриваемого объема. Тогда общее количество энергии, внесенной потоком в рассматриваемый участок за время ∆t через сечение I—I, будет равно:
Аналогично можно получить суммарную энергию, вынесенную потоком через сечение II—II за время ∆t:
По закону сохранения энергии суммарная энергия, внесенная через сечение I—I, при установившемся движении должна быть равна суммарной энергии, вынесенной через сечение II—II, с учетом затрат энергии на преодоление гидравлических сопротивлений при движении жидкости от сечения I—I к сечению II—II. Затраченную энергию можно выразить в виде произведения веса рассматриваемого объема на некоторую высоту (потери высоты):
Тогда:
Так как, согласно уравнению постоянства расхода, Q1=Q2=Q и, кроме того,
Или, заменяя ρg на γ:
Отнесем все члены уравнения (1.44) к единице веса, для чего разделим их на γQ. Тогда
или в общем виде:
Следовательно, для всех сечений потока можно записать:
где z — расстояние от плоскости сравнения до центра тяжести сечения; р — давление в центре тяжести в этом сечении; υ — средняя скорость в этом сечении; hпот — удельная энергия, затраченная на преодоление сопротивлений от начального до рассматриваемого сечения. Удельная механическая энергия потока в любом его сечении равна:
Уравнение (1.47) носит наименование уравнения Бернулли. В приведенном выводе этого уравнения скорости движения отдельных частиц жидкости в пределах живого сечения приняты одинаковыми и равными средней скорости. Если учитывать неравномерность распределения скоростей по живому сечению, то уравнение (1.47) получает следующий вид:
Рис.1.22. Схема, поясняющая понятие скоростного напора Коэффициент a учитывает влияние неравномерности распределения скоростей по сечению на удельную кинетическую энергию потока, вычисленную по средней скорости (см. § 20 и 21). Коэффициент a называют коррективом кинетической энергии или коэффициентом Кориолиса. Сумма первых двух членов уравнения (1.47а) Геометрический и энергетический смысл уравнения Бернулли. Все члены уравнения Бернулли выражаются в единицах длины, поэтому каждый из них может называться высотой: z — геометрическая высота, или высота положения; р/γ — пьезометрическая высота, или высота гидродинамического давления;
hпот — высота, соответствующая потерям напора. Следовательно, геометрический смысл уравнения Бернулли может быть сформулирован так: при установившемся движении жидкости сумма четырех высот (высоты положения, пьезометрической высоты, высоты, соответствующей скоростному напору, и высоты, соответствующей потерям напора) остается неизменной вдоль потока. Кроме того, каждый из членов уравнения Бернулли выражает удельную энергию потока, т. е. энергию, приходящуюся на единицу веса движущейся жидкости: z — удельная энергия положения; р/γ — удельная энергия гидродинамического давления;
hпот — потери удельной энергии. Тогда энергетический смысл уравнения Бернулли можно сформулировать следующим образом: при установившемся движении жидкости сумма четырех удельных энергий (энергии положения, энергии гидродинамического давления, кинетической энергии и потерь энергии) остается неизменной вдоль потока. Если в каком-либо сечении потока жидкости (рис. 1.22) установить две трубки — пьезометрическую 1 и скоростную 2, нижний изогнутый конец которой направлен против течения, то в скоростной трубке создается дополнительное давление от воздействия скорости движущейся жидкости. Высота подъема жидкости в скоростной трубке больше высоты подъема жидкости в пьезометрической трубке на скоростной напор Все члены уравнения Бернулли представлены графически на рис. 1.23. Здесь в четырех выбранных сечениях потока SS установлены пьезометрические и скоростные трубки. Если соединить уровни жидкости в пьезометрах, то получим пьезометрическую линию, или линию потенциальной удельной энергии. Она находится на расстоянии z+ р/γ от плоскости сравнения.
Рис. 1.23. Графическое изображение членов уравнения Бернулли 1 — напорная линия, или линия суммарной удельной энергии; 2 — пьезометрическая линия или линия потенциальной удельной энергии; 3 — линия плоскости сравнения Падение этой линии на единицу длины называется пьезометрическим уклоном J. Соединяя уровни жидкости в скоростных трубках, получим напорную линию или линию, суммарной (потенциальной и кинетической) удельной энергии. Падение напорной линии на единицу длины называется гидравлическим уклоном i и характеризует потери напора на единицу длины. Из рис. 1.23 видно, что с удалением от начального сечения I потери напора возрастают. ПРАКТИЧЕСКОЕ ПРИЛОЖЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ На основании уравнения Бернулли сконструирован ряд приборов, таких как водомер Вентури, водоструйный насос, эжектор и пр. На рис. 1.24 показан горизонтальный трубопровод диаметром D, на котором устроено сужение диаметром d. В нормальной и суженной частях установлены два пьезометра (в сечениях /—/ и //—//).
Ж
Рис. 1.24. Схема водомера Вентури Пренебрегая потерями напора между сечениями I—I и II—II, а также неравномерностью распределения скоростей по сечению (a = 1) и принимая, что плоскость сравнения 00 проходит через ось трубопровода, можем записать уравнение Бернулли в таком виде:
Отсюда следует, что с увеличением скорости движения давление должно уменьшаться и, наоборот, с уменьшением скорости давление должно увеличиваться. Это положение используется в водомере Вентури, где по разности показаний пьезометров h (см. рис. 1.24), зная диаметры D и d, можно определить расход. В водоструйном насосе (рис. 1.25) вода из бака I поступает в трубопровод, имеющий сужение. В узком сечении скорость струи возрастает, и. струя увлекает за собой воздух, находящийся в смесительной камере, благодаря чему происходит подсасывание жидкости по трубке, опущенной в бак 2. При больших скоростях движения жидкость будет подсасываться из бака 2 непрерывно. По этому же принципу работают эжекторы и гидроэлеваторы.
|
||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.67.32 (0.006 с.) |


 Потенциальная энергия положения этого объема равна:
Потенциальная энергия положения этого объема равна: (1.40)
(1.40)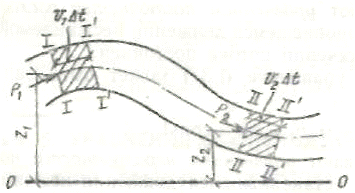
 (I.41)
(I.41) Рассматриваемый объем обладает также потенциальной энерги-1 ей давления. Представим, что в сечении I—I имеется поршень, движущийся со скоростью 1>1 в направлении сечения II—II. Этот поршень за время ∆t пройдет путь υ1∆t. Сила давления на этот поршень равна
Рассматриваемый объем обладает также потенциальной энерги-1 ей давления. Представим, что в сечении I—I имеется поршень, движущийся со скоростью 1>1 в направлении сечения II—II. Этот поршень за время ∆t пройдет путь υ1∆t. Сила давления на этот поршень равна  . Следовательно, произведенная поршнем работа будет равна:
. Следовательно, произведенная поршнем работа будет равна: (I.42)
(I.42)
 .
. (1.43)
(1.43) .
. , можем написать:
, можем написать:
 (I.44)
(I.44)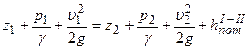 (1.45)
(1.45)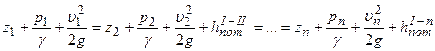 (I.46)
(I.46) , (I.47)
, (I.47)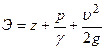
 (1.47а)
(1.47а)
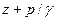 —пьезометрический напор, по аналогии
—пьезометрический напор, по аналогии 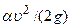 — скоростной напор, а hпот — потерянный напор. Сумму первых трех членов уравнения Бернулли
— скоростной напор, а hпот — потерянный напор. Сумму первых трех членов уравнения Бернулли 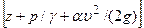 называют полным напором.
называют полным напором.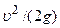 — высота, соответствующая скоростному напору;
— высота, соответствующая скоростному напору;


 . (1.48)
. (1.48)


