
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Давление жидкости на плоские поверхности. Центр давления. Эпюра давленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
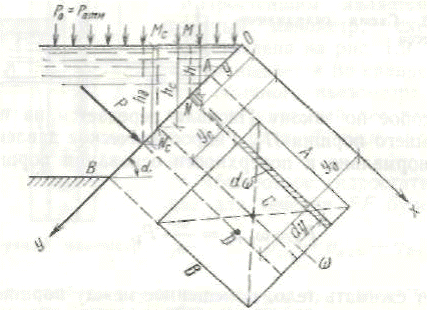
Предположим, что необходимо определить силу полного гидростатического давления, действующего на плоскую прямоугольную фигуру АВ площадью ω, взятую на стенке ВО, наклоненной к горизонту под углом a (рис. I.11). Проекцию фигуры АВ на плоскость чертежа примем за ось координат у.
Рис. 1.11. Схема давления жидкости на плоскую фигуру Продолжим линию AВ до пересечения с уровнем свободной поверхности жидкости в точке О, которую будем считать за начало координат. Линия Ох, перпендикулярная направлению АВ, будет в нашей системе осью х. Мысленно повернув фигуру А В вокруг оси у до совмещения с плоскостью чертежа, выделим на площади со бесконечно малую полоску шириной dу. Эта полоска, погруженная в жидкость на глубину h, находится на расстоянии у от оси х и имеет бесконечно малую площадь dω. Элементарная сила абсолютного гидростатического давления, действующего на рассматриваемую полоску, будет равна:
Из треугольника ОМN, у которого сторона МN равна h, а сторона N0 равна у, находим: h = уsina. Тогда
Проинтегрировав это выражение по площади ω, получим силу полного абсолютного гидростатического давления, действующего на плоскую фигуру А В:
Интеграл тяжести до оси х находим из треугольника ОМСNc. (см. рис. I.11):
Таким образом, сила полного гидростатического давления на плоскую фигуру равна абсолютному гидростатическому давлению в центре тяжести этой фигуры рc, умноженному на площадь фигуры ω. В открытом резервуаре, где р0 = ратм, сила полного гидростатического давления, действующего на плоскую фигуру, равна произведению площади фигуры ни избыточное гидростатическое давление в ее центре тяжести. Центром давления называется точка приложения силы избыточного гидростатического давления Известно, что элементарная сила избыточного давления определяется как
где
Тогда
Из уравнения (1.20) следует, что центр давления лежит ниже центра тяжести фигуры на расстоянии эксцентриситета
Рис. 1.12. Эпюры гидростатического давления, Рис. 1.13. Эпюры гидростатического давления, действующего на вертикальную стенку действующего на наклонную стенку 1— абсолютное давление; 1 — 2 - избыточное давление абсолютное давление: 2 — избыточное давление Для графического изображения закона изменения гидростатического давления по глубине служат эпюры давления. Площадь эпюры выражает силу давления, а центр тяжести эпюры — это точка, через которую проходит равнодействующая сила давления. При построении эпюр учитывают, что давление направлено нормально к стенке, а уравнение р = р0 + уh, характеризующее распределение гидростатического давления по глубине, является уравнением прямой. На рис. 1.12 показаны эпюры гидростатического давления (абсолютного и избыточного), действующего на вертикальную плоскую стенку АВ. Для их построения достаточно отложить в выбранном масштабе гидростатическое давление по горизонтальному направлению, совпадающему с направлением гидростатического давления, на поверхности жидкости и у дна, соединив концы этих отрезков прямой линией. Из рассмотрения рис. 1.12 следует, что эпюра абсолютного гидростатического давления представляет собой трапецию, а эпюра избыточного гидростатического давления — треугольник. Если плоская стенка АВ, на которую действует жидкость, наклонена к горизонту под углом а (рис. 1.13), то основное уравнение гидростатики принимает следующий вид:
Таким образом, при наклонной стенке эпюры абсолютного и избыточного гидростатического давления представляют собой соответственно наклонную трапецию и наклонный треугольник. Таким образом, при наклонной ' стенке эпюры абсолютного и избыточного гидростатического давления представляют собой соответственно наклонную трапецию и наклонный треугольник. Рассмотрим теперь эпюру избыточного гидростатического давления для вертикальной плоской стенки АВ, подверженной действию воды с двух сторон (рис. 1.14). В данном случае на вертикальную стенку будут действовать параллельные и противоположно направленные силы гидростатического давления, поэтому силы, действующие справа налево, будут вычитаться из сил, действующих слева направо. Получающаяся в результате эпюра ОМNВ представляет собой вертикальную трапецию.
Эпюра гидростатического давления на горизонтальное дно резервуара представляет собой прямоугольник, так как при постоянной глубине к избыточное гидростатическое давление на дно
|
||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.123.194 (0.009 с.) |



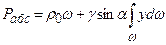
 выражает статический момент площади фигуры A В относительно оси х, т. е.
выражает статический момент площади фигуры A В относительно оси х, т. е.  . Расстояние уc. от центра
. Расстояние уc. от центра . Здесь hc — глубина погружения центра тяжести площади ω в жидкость. Следовательно,
. Здесь hc — глубина погружения центра тяжести площади ω в жидкость. Следовательно, (I.18)
(I.18) . Для нахождения ординаты центра давления уД воспользуемся свойством момента равнодействующей, который относительно любой оси должен быть равен сумме элементарных моментов составляющих ее сил относительно той же оси (теорема Вариньона),т.е.
. Для нахождения ординаты центра давления уД воспользуемся свойством момента равнодействующей, который относительно любой оси должен быть равен сумме элементарных моментов составляющих ее сил относительно той же оси (теорема Вариньона),т.е.  . На основании упомянутой теоремы напишем
. На основании упомянутой теоремы напишем  , откуда
, откуда 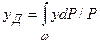 .
. , а равнодействующая этих сил
, а равнодействующая этих сил  . Тогда значение ординаты центра давления уД будет равно:
. Тогда значение ординаты центра давления уД будет равно: , (1.19)
, (1.19) ,как известно, есть момент инерции I, фигуры АВ относительно оси x. Применяя для него формулу перехода к оси,
,как известно, есть момент инерции I, фигуры АВ относительно оси x. Применяя для него формулу перехода к оси,  проходящей через центр тяжести С, получим:
проходящей через центр тяжести С, получим: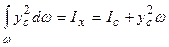
 (I.20)
(I.20)

 (I.21)
(I.21)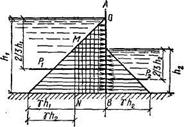
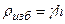 является постоянным.
является постоянным.


