
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резкое расширение трубопровода.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Как показывают наблюдения, поток, выходящий из узкой трубы, отрывается от стенок и дальше движется в виде струи, отделенной от остальной жидкости поверхностью раздела (см. рис. 4.14). На поверхности раздела возникают вихри, которые отрываются и переносятся далее транзитным потоком. Между транзитным потоком и водоворотной зоной происходит массообмен, но он незначителен. Струя постепенно расширяется и на некотором расстоянии от начала расширения заполняет все сечение трубы. Вследствие отрыва потока и связанного с этим вихреобразования на участке трубы наблюдаются значительные потери напора. Постепенное расширение. Если расширение происходит постепенно (см. рис. 4.15), то потери напора значительно уменьшаются. При течении жидкости в диффузоре скорость потока постепенно уменьшается, уменьшается кинетическая энергия частиц, но увеличивается градиент давления. При некоторых значениях угла расширения α частицы у стенки не могут преодолеть увеличивающееся давление и останавливаются. При дальнейшем увеличении угла частицы жидкости могут двигаться против основного потока, как при резком расширении. Происходит отрыв основного потока от стенок и вихреобразование. Интенсивность этих явлений возрастает с увеличением угла α и степенью расширения Внезапное сужение. При внезапном сужении потока (см. рис. 4.16) также образуются водоворотные зоны в результате отрыва от стенок основного потока, но они значительно меньше, чем при резком расширении трубы, поэтому и потери напора значительно меньше. Коэффициент местного сопротивления на внезапное сужение потока можно определить по формуле
Постепенное сужение (конфузор). Величина сопротивления конфузора будет зависеть от угла конусности конфузора θ. Коэффициент сопротивления можно определить по формуле
Поворот трубы (колено). В результате искривления потока на вогнутой стороне внутренней поверхности трубы давление больше, чем на выпуклой. В связи с этим жидкость движется с различной скоростью, что способствует отрыву от стенок пограничного слоя и потерям напора (см. рис. 4.17). Величина коэффициента местного сопротивления
Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости[3] через элемент гидравлической системы пропорциональны квадрату скорости жидкости[2]. По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ζ[4], которая называется коэффициент потерь или коэффициент местного сопротивления и такова, что
22. Внезапное расширение и сужение потока (теорема Борда). При внезапном расширении потока в трубке от сечения 1 до сечения 2 жидкость не течёт по всему контуру стенок, а движется по плавным линиям токов. Вблизи стенок, где внезапно увеличивается диаметр трубы, образуется пространство, в котором жидкость находится в интенсивном вращательном движении. При таком интенсивном перемешивании происходит очень активное трение жидкости о твёрдые стенки трубы об основное русла потока, а также трение внутри вращающихся потоков, вследствие чего происходят существенные потери энергии. Кроме того, какая-то часть энергии жидкости затрачивается на фазовый переход частиц жидкости из основного потока во вращательные и наоборот. На рисунке видно, что показания пьезометра во втором сечении больше, чем в первом. Тогда появляется вопрос, о каких потерях идёт речь? Дело в том, что показания пьезометра зависят не только от потерь энергии, но и от величины давления. А давление во втором сечении становится больше из-за уменьшения скоростного напора за счёт расширения потока и падения скорости. В этом случае надо учитывать, что если бы не было потерь напора на местном сопротивлении, то высота жидкости во втором пьезометре была бы ещё больше.
Назвав разность
23. Трубопроводная арматура. Определение местных сопротивлений. Трубопроводная арматура — устройство, устанавливаемое на трубопроводах, агрегатах, сосудах и предназначенное для управления (отключения, распределения, регулирования, сброса, смешивания, фазоразделения) потоками рабочих сред (жидкой, газообразной, газожидкостной,порошкообразной, суспензии и т. п.) путем изменения площади проходного сечения. По области применения · Пароводяная; · Газовая; · Нефтяная; · Энергетическая; · Химическая; · Судовая; · Резервуарная.
Местными гидравлическими сопротивлениями называются любые участки гидравлической системы, где имеются повороты, преграды на пути потока рабочей жидкости, расширения или сужения, вызывающие внезапное изменение формы потока, скорости или направления ее движения. В этих местах интенсивно теряется напор. Примерами местных сопротивлений могут быть искривления оси трубопровода, изменения проходных сечений любых гидравлических аппаратов, стыки трубопроводов и т.п. Потери напора на местных сопротивлениях
где Коэффициент местного сопротивления зависит от конкретных геометрических размеров местного сопротивления и его формы. В связи со сложностью процессов, которые происходят при движении жидкости через местные сопротивления, в большинстве случаев его приходится определять на основании экспериментальных данных. Однако в некоторых случаях величины коэффициентов местных сопротивлений можно определить аналитически. Из определения коэффициента Коэффициенты различных сопротивлений можно найти в гидравлических справочниках. В том случае, если местные сопротивления находятся на расстоянии меньше (25ч50)d друг от друга (
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1996; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

 .
. , где
, где 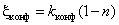 ,
,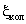 зависит от угла поворота θ, радиуса поворота R, формы поперечного сечения и приводится в справочниках. Для круглого сечения трубы при θ= 90º. коэффициент сопротивления можно определить по формуле
зависит от угла поворота θ, радиуса поворота R, формы поперечного сечения и приводится в справочниках. Для круглого сечения трубы при θ= 90º. коэффициент сопротивления можно определить по формуле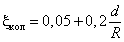


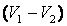 потерянной скоростью, можно сказать, что потеря напора при внезапном расширении равна скоростному напору, подсчитанному по потерянной скорости. Это утверждение носит имя теоремы Борда - Карно.
потерянной скоростью, можно сказать, что потеря напора при внезапном расширении равна скоростному напору, подсчитанному по потерянной скорости. Это утверждение носит имя теоремы Борда - Карно.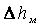 определяются по формуле Вейсбаха:
определяются по формуле Вейсбаха: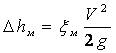 ;
;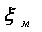 - коэффициент местного сопротивления.
- коэффициент местного сопротивления.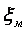 видно, что он учитывает все виды потерь энергии потока жидкости на участке местного сопротивления. Его физический смысл состоит в том, что он показывает долю скоростного напора, затрачиваемого на преодоление данного сопротивления.
видно, что он учитывает все виды потерь энергии потока жидкости на участке местного сопротивления. Его физический смысл состоит в том, что он показывает долю скоростного напора, затрачиваемого на преодоление данного сопротивления.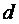 - диаметр трубопровода, соединяющего местные сопротивления), весьма вероятно их взаимное влияние друг на друга, а их действительные коэффициенты местных сопротивлений будут отличаться от табличных. Такие сопротивления нужно рассматривать как единое сложное сопротивление, коэффициент
- диаметр трубопровода, соединяющего местные сопротивления), весьма вероятно их взаимное влияние друг на друга, а их действительные коэффициенты местных сопротивлений будут отличаться от табличных. Такие сопротивления нужно рассматривать как единое сложное сопротивление, коэффициент  которого определяется только экспериментально. Нужно отметить, что из-за взаимного влияния местных сопротивлений, расположенных вблизи друг друга в потоке, во многих случаях суммарная потеря напора не равна простой сумме потерь напора на каждом из этих сопротивлений.
которого определяется только экспериментально. Нужно отметить, что из-за взаимного влияния местных сопротивлений, расположенных вблизи друг друга в потоке, во многих случаях суммарная потеря напора не равна простой сумме потерь напора на каждом из этих сопротивлений.


