Общие сведения о гидравлических сопротивлениях

Определение потерь напора – одна из основных задач практически любого гидравлического расчета. Однако необходимо отметить, что исследование гидравлических сопротивлений возможно только для установившегося движения жидкости. Для неустановившегося движения нет способов их определения, поэтому в гидравлике результаты исследований сопротивлений установившегося движения переносят и на неустановившееся движение.

Для определения давления и средней скорости в различных сечениях потока жидкости выше были выведены уравнение Бернулли и уравнение сплошности в гидравлической форме (уравнение сплошности), которые могут быть записаны в следующем виде:

z+pγ+αV22g+hω=H; Q = Vw.

(7.1)

В практических задачах, которые решаются с помощью расчетного аппарата гидравлики, обычно известны или могут быть определены из заданных величин напор H и расход Q. Известно также положение центра тяжести рассматриваемых сечений относительно плоскости сравнения, их площади. Таким образом, в этих уравнениях остаются три неизвестных: V, p, h _ω. Для их определения систему (7.1) необходимо дополнить третьим уравнением, связывающим между собой неизвестные величины. Такая зависимость вытекает из закона Ньютона для касательных напряжений.

Эту зависимость в общем виде можно записать так:

h ω = f (V).

(7.2)

Давно установлено, что потери энергии потока жидкости при его движении вызываются как наличием сил трения, направленных в сторону противоположную направлению движения жидкости, так и изменением условий ее движения (протекание жидкости через разного рода препятствия, изменение сечения потока и т. д.). Поэтому потери энергии (напора) можно классифицировать следующим образом:

Потери напора, затрачиваемые на преодоление сил трения, называются потерями напора на трение или потерями напора по длине.

Потери напора, вызванные изменением конфигурации границ потока (затрачиваемые на преодоление формы) называют местными потерями напора или местными сопротивлениями.

Таким образом, общую потерю напора рассматривают как сумму потерь напора, вызванных каждым сопротивлением в отдельности, то есть принимают:

h пот = Σ h дл + Σ h м.

(7.3)

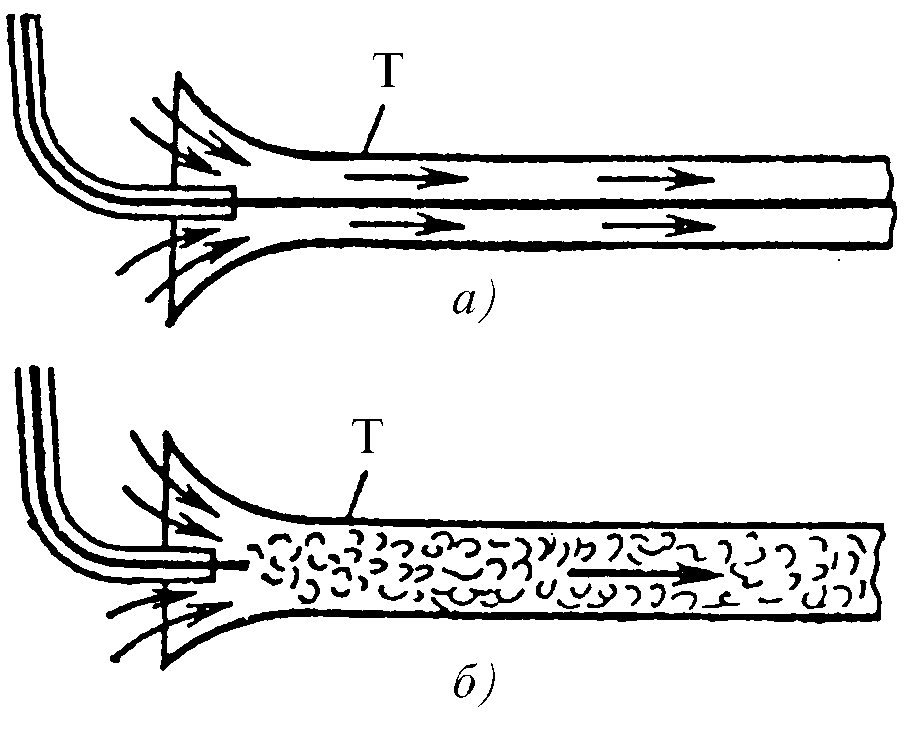
где:

Σ h _дл — сумма всех потерь по длине отдельных последовательно расположенных участков;

Σ h _м — сумма всех потерь напора на преодоление местных сопротивлений.

Ламинарный и турбулентный режим движения

Режим движения, при котором отсутствуют пульсации скорости и перемешивание частиц, называется ламинарным (от латинского слова lamina слой) режимом движения.

Режим движения, характерной особенностью которого является пе­ремешивание частиц и пульсации скорости, называется турбулентным (от латинского слова turbulentus беспорядочный) режимом движения.

Рис. 1.31. Характерные особенности ламинарного (а) и турбулентного (б) режимов движения жидкости

Ламинарный режим движения встречается чаще всего при движении по трубам жидкостей с большой вязкостью (нефти, нефтепродуктов и т.д.), а также при движении воды в тонких капиллярных трубках и порах грунта.

Турбулентный режим встречается в большинстве случаев гидротехнической и гидромелиоративной практики (движение воды в трубах, каналах, реках и т.п.).

Многочисленные экспериментальные данные подтверждают, что при разных режимах движения жидкости потери энергии по разному зависят от скорости движения.

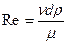Количественный критерий, позволяющий предсказать характер (лам. или турб.) течения. . С учетом зависимости между кинематическим и динамическим коэф. вязкости . Число является мерой отношения кин.энергии жид-ти к работе сил вязкого трения и от него зависят все безразмерные коэф., входящие в расчетные зависимости. Переход от лам. режима к турб. Совершается при числах Re>2300. При значениях Reкр. Критическое знач. используется не только при круговом, но и любом др. сечении потока; подсчет значения числа производят заменяя диаметр на гидравлический радиус, т.е.d=4R