
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерпретация уравнения Бернулли для идеальной и реальной жидкости с геометрической и энергетической точек зрения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Как и в гидростатике, величину Z называют геометрической (нивелирной) высотой. Второе слагаемое ‑ p/ρg носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре. Сумма первых двух членов уравнения z+ p/ρg гидростатический напор. Третье слагаемое уравнения Бернулли Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н. Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически. Значения Из уравнения Бернулли для струйки невязкой жидкости (и графика) следует, что гидродинамический напор по длине струйки постоянен. Энергетическая интерпретация уравнения Бернулли Суммарной энергетической характеристикой жидкости является её гидродинамический напор.
6.2 Графическое представление уравнения Бернулли С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости.
Здесь с энергетической точки зрения (в единицах энергии, Дж/кг) Умножив все члены уравнения на удельный вес жидкости
Коэффициент Кориолиса. Графическое представление уравнения Бернулли. Коэффициент кинетической энергии потока (коэффициент Кориолиса) - отношение действительной удельной величины кинетической энергии потока к величине удельной кинетической энергии, вычисленной в предположении, что скорости во всех точках живого сечения равны средней скорости. Следовательно, величина α(альфа) является коэффициентом Кориолиса или коррективом при расчете по энергии и выражает отношение действительной энергии к ее значению, определяемому по средней скорости. Значения коэффициента гидравлического трения К и коэффициента Кориолиса а изменяются по длине начального участка в значительных пределах.
Обычно определяется опытным путём на основании измерений скорости в разных точках потока. Для ламинарного движ. α=2, для турбулентного α=1.045 до 1.10
Геометрическое представление ур. Бернулли
Графическое представление уравнения Бернулли Линия соединяющая отметки показаний называется пьезометрической линией z+ p/ρg – пьезометрический напор hυ=αυ^2/2g – скоростной напор Сумма пьезометрического и скоростного называется напорной линией, а её уклон называется гидродинамическим(У) Потерянная высота
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 815; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.180 (0.008 с.) |

 называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость v при отсутствии сопротивления движению.
называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость v при отсутствии сопротивления движению. - геометрическую, пьезометрическую и скоростную высоты можно определить для каждого сечения элементарной струйки жидкости. Геометрическое место точек, высоты которых равны z+ p/ρg, называется пьезометрической линией. Если к этим высотам добавить скоростные высоты, равные
- геометрическую, пьезометрическую и скоростную высоты можно определить для каждого сечения элементарной струйки жидкости. Геометрическое место точек, высоты которых равны z+ p/ρg, называется пьезометрической линией. Если к этим высотам добавить скоростные высоты, равные 
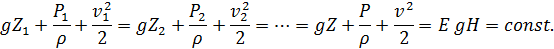
 ‑ удельная потенциальная энергия положения;
‑ удельная потенциальная энергия положения; 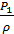 ‑ удельная потенциальная энергия давления;
‑ удельная потенциальная энергия давления; 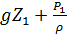 ‑ удельная потенциальная энергия;
‑ удельная потенциальная энергия;  ‑ удельная кинетическая энергия; v ‑ скорость элементарной струйки идеальной жидкости.
‑ удельная кинетическая энергия; v ‑ скорость элементарной струйки идеальной жидкости. , получим
, получим
 ‑ весовое давление, Па; P — гидродинамическое давление, Па;
‑ весовое давление, Па; P — гидродинамическое давление, Па;  ‑ динамическое давление Па;
‑ динамическое давление Па;  ‑ полное давление, Па
‑ полное давление, Па
 складывается из потерь по длине, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)
складывается из потерь по длине, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока) = hлин + hмест
= hлин + hмест 


