
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы справедливые для идеальной жидкостиСодержание книги
Поиск на нашем сайте
Уравнение неразрывности струи Так как жидкость несжимаема (плотность всюду одинаковая), то через любое сечение трубы в единицу времени протекают одинаковые объемы жидкости.
где
Уравнение Бернулли Основано на теореме: изменение полной энергии системы равно работе внешних сил, если не учитывать силы трения внутри системы.
где
Согласно уравнению Бернулли давление в потоке жидкости выше там, где скорость меньше и наоборот. Законы течения вязких жидкостей Вязкость (внутренние трение) жидкости – свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой. Основной закон вязкой жидкости был установлен И. Ньютоном (1687 г.) – формула Ньютона
Наряду с динамическим коэффициентом вязкости рассматривают кинематический коэффициент вязкости Жидкости делятся по вязким свойствам на два вида: ньютоновские и неньютоновские. Ньютоновской называется жидкость, коэффициент вязкости которой зависит только от природы и температуры. Для ньютоновских жидкостей Неньютоновской называется жидкость, коэффициент вязкости которой зависит не только от природы вещества и температуры, но и от условий течения жидкости, в частности, от градиента скорости. Коэффициент вязкости в этом случае не является константой. При этом вязкость жидкости характеризуется условным коэффициентом вязкости, который зависит от определенных условий течения жидкости (например, давления, скорости). Зависимость силы вязкости от градиента скорости становится нелинейной. Кровь – неньютоновская жидкость. В наибольшей степени это связано с тем, что она обладает внутренней структурой, представляя собой суспензию форменных элементов в растворе – плазме. Плазма – практически ньютоновская жидкость. Поскольку 93% форменных элементов составляют эритроциты, то при упрощенном рассмотрении – кровь – это суспензия эритроцитов в физиологическом растворе. Таким образом, внутренняя структура крови, а следовательно её вязкость, оказывается неодинаковой вдоль кровеносного русла в зависимости от условий течения. Режимы течения крови разделяют на ламинарное и турбулентное Ламинарное – это упорядоченное течение жидкости, при котором она перемещается слоями, параллельными направлению течения. При ламинарном течении скорость в сечении трубы изменяется по параболическому закону:
где
Режим течения жидкости характеризуется числом Рейнольдса:
где
Если значение
Турбулентное течение связано с дополнительной затратой энергии, поэтому в кровеносной системе это может привести к дополнительной нагрузке на сердце. Шум, возникающий при турбулентном течении крови, может быть использован для диагностики заболеваний.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.31 (0.005 с.) |

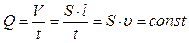 ,
,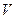 – объем,
– объем,  – площадь поперечного сечения трубы,
– площадь поперечного сечения трубы, – линейная скорость течения жидкости.
– линейная скорость течения жидкости. .
. ,
, – статическое давление,
– статическое давление, – гидростатическое давление,
– гидростатическое давление, – гидродинамическое давление.
– гидродинамическое давление.
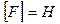 – сила внутреннего трения;
– сила внутреннего трения; – динамический коэффициент вязкости;
– динамический коэффициент вязкости; – градиент скорости, показывающий на сколько изменилась скорость при изменении на единицу расстояния в направления ОХ при переходе от слоя к слою (скорость сдвига);
– градиент скорости, показывающий на сколько изменилась скорость при изменении на единицу расстояния в направления ОХ при переходе от слоя к слою (скорость сдвига); – площадь соприкасающихся слоев.
– площадь соприкасающихся слоев. крови в норме = 0,004 – 0,005 Па . с.
крови в норме = 0,004 – 0,005 Па . с. (
(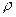 – плотность жидкости).
– плотность жидкости). ~
~  . Для них справедлива формула Ньютона, в которой коэффициент вязкости является постоянным параметром, не зависящим от условий течения жидкости.
. Для них справедлива формула Ньютона, в которой коэффициент вязкости является постоянным параметром, не зависящим от условий течения жидкости. ,
, – радиус трубы,
– радиус трубы, 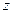 – расстояние от оси,
– расстояние от оси,  – максимальная скорость.
– максимальная скорость. С увеличением скорости движения ламинарное течение переходит в турбулентное, при котором происходит интенсивное перемешивание между слоями жидкости, в потоке возникают хаотические движения по сложным траекториям. Для турбулентного течения характерно нерегулярное, беспорядочное изменение скорости со временем в каждой точке потока.
С увеличением скорости движения ламинарное течение переходит в турбулентное, при котором происходит интенсивное перемешивание между слоями жидкости, в потоке возникают хаотические движения по сложным траекториям. Для турбулентного течения характерно нерегулярное, беспорядочное изменение скорости со временем в каждой точке потока.
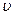 – средняя скорость жидкости по поперечному сечению;
– средняя скорость жидкости по поперечному сечению; – диаметр трубы;
– диаметр трубы; 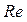 меньше критического, то имеет место ламинарное течение жидкости, если больше – течение становится турбулентным.
меньше критического, то имеет место ламинарное течение жидкости, если больше – течение становится турбулентным.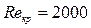 (для крови),
(для крови),  (для воды).
(для воды).


