
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение установившегося уровня жидкости в промежуточной ёмкости CСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для определения установившегося уровня жидкости в промежуточной ёмкости
где р – давления в сечениях А-А и В-В соответственно (Па);
g – ускорение свободного падения g = 9,81м/  ; ;
Рисунок 4 – К определению уровня
Зная расход можно определить
Подставляя (33) в (32) получим:
В действительности при прохождении жидкости через насадок в нем возникают потери напора, учтём их с помощью коэффициента расхода
Для цилиндрического внешнего насадка коэффициент расхода
4.5 Определение разности показаний манометров Рм2 и Рм3 Для сечений Рм2 и Рм3 уравнение Бернулли имеет вид:
где
g – ускорение свободного падения (м/с2);
Рисунок 5 – Манометры Рм2 и Рм3 Выберем ось трубопровода за начало отсчета, тогда Потери напора между выбранными сечениями
Потери напора по длине трубопровода определяются по формуле Дарси-Вейсбаха:
Подставим (39) в (38):
Подставив в (41) значения параметров получим при
Определение суммарных потерь напора в местных
|
|||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.113.71 (0.006 с.) |

 составим уравнение Бернулли для сечений 1–1 и 2–2 (рис.4):
составим уравнение Бернулли для сечений 1–1 и 2–2 (рис.4):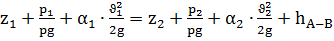 (31)
(31) – расстояние от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);
– расстояние от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м); – плотность циркулирующей жидкости (кг/м3);
– плотность циркулирующей жидкости (кг/м3);
 скорость течения жидкости в сечении 1–1 и 2–2 соответственно (м/с);
скорость течения жидкости в сечении 1–1 и 2–2 соответственно (м/с); коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях 1–1 и 2–2 соответственно.
коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях 1–1 и 2–2 соответственно.  потери напора на участках между выбранными сечениями. Плоскость сравнения совместим с сечением 2-2, тогда
потери напора на участках между выбранными сечениями. Плоскость сравнения совместим с сечением 2-2, тогда 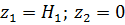 . Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора
. Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора  ,
,  (для практических расчетов).Т. к. диаметр промежуточной ёмкости во многом больше диаметра насадки
(для практических расчетов).Т. к. диаметр промежуточной ёмкости во многом больше диаметра насадки  значит
значит  .
. , т.к емкость открытая. Запишем уравнение Бернулли (31) с учётом всех утверждений:
, т.к емкость открытая. Запишем уравнение Бернулли (31) с учётом всех утверждений: (32)
(32) :
: (33)
(33) (34)
(34) , подставив его в формулу (34) получим:
, подставив его в формулу (34) получим: (35)
(35) . Тогда для нашего случая при
. Тогда для нашего случая при  получим:
получим: (36)
(36) (37)
(37) расстояние от сечений Рм2 и Рм3 соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);
расстояние от сечений Рм2 и Рм3 соответственно до некоторой произвольно выбранной горизонтальной плоскости (м); – давления в сечениях Рм2 и Рм3 соответственно (Па);
– давления в сечениях Рм2 и Рм3 соответственно (Па);
 скорость течения жидкости в сечении Рм2 и Рм3 соответственно (м/с);
скорость течения жидкости в сечении Рм2 и Рм3 соответственно (м/с); потери напора на участках между выбранными сечениями.
потери напора на участках между выбранными сечениями.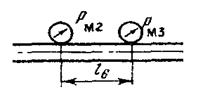
 , т.к трубопровод горизонтален.
, т.к трубопровод горизонтален.  , (для практических расчетов).
, (для практических расчетов). определяются только потерями напора по длине трубопровода, т.к местных сопротивлений на данном участке нет;
определяются только потерями напора по длине трубопровода, т.к местных сопротивлений на данном участке нет;  , т.к расход и площадь поперечного сечения одинаковы для сечений Рм2 и Рм3. В итоге формула (37) примет вид:
, т.к расход и площадь поперечного сечения одинаковы для сечений Рм2 и Рм3. В итоге формула (37) примет вид: ;
; 
 (38)
(38) (39)
(39) (40)
(40)
 (41)
(41)

 =760
=760 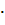 0,0228
0,0228 



