
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет циркулярной установкиСодержание книги
Поиск на нашем сайте 4.1 Определение геометрической высоты всасывания насоса H2 Для определения геометрической высоты воспользуемся известным уравнением Бернулли. Для его применения необходимо выбрать плоскость сравнения. Плоскостью сравнения может служить любая горизонтальная плоскость. Также необходимо выбрать два сечения. Сечения проводятся перпендикулярно вектору скорости. Нумерация сечений производится по направлению движения жидкости. Уравнение Бернулли для установившегося движения реальной несжимаемой жидкости записывается:
где: z– высоты от выбранных сечений соответственно до выбранной плоскости сравнения (м). Если сечение лежит ниже плоскости сравнения, то z отрицательна. р – абсолютное или манометрическое давление в сечениях (Па); ρ – плотность несжимаемой жидкости (кг/м³); α – коэффициент кинетической энергии (коэффициент Кориолиса). Обычно принимается равным единице.
g – ускорение свободного падения (м/с²); h1-2 – потери напора между сечениями. Они представляют собой сумму потерь напора по длине и сумму потерь напора на местных сопротивлениях: h1-2 = hм + hд На схеме циркуляционной установки удобно выбрать два сечения, где: А-А– по поверхности жидкости в нижнем резервуаре В; В-В – в месте установки вакуумметра Рв во всасывающей линии насосной установки. Тогда уравнение Бернулли для этих сечений запишется в виде:
где ZA-A и ZB-B – расстояния от сечений А–А и В–В соответственно до некоторой произвольно выбранной горизонтальной плоскости; РA-A, РB-B – давления в сечениях А–А и В–В соответственно; ρ – плотность циркуляционной жидкости; g – ускорение свободного падения;
HA-B –потери напора на участках между выбранными сечениями. Если выбрать поверхность жидкости в нижнем резервуаре за начало отсчета, т.е. сечение А–А, тогда ZA-A=О, а ZB-B=H2. Поскольку в нижнем резервуаре (В) уровень установившийся, значение скорости
где Q – расход жидкости (м³/с); S – площадь поперечного сечения (м²); В результате, формула (2) примет вид:
В полученной формуле известны все величины, кроме Н2 и hA-B. Поэтому для определения геометрической высоты всасывания насоса (Н2) предварительно необходимо определить hA-B.
|
||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.005 с.) |

 (1)
(1) – средняя скорость в сечениях (м/с);
– средняя скорость в сечениях (м/с);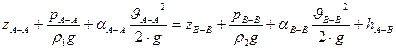 (2)
(2) (3)
(3)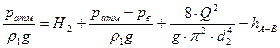 (4)
(4)


